Dr. Vadym Zayets
v.zayets(at)gmail.com
My Research and Inventions
click here to see all content |

Dr. Vadym Zayetsv.zayets(at)gmail.com |
|
 |
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionScatteringsSpin-polarized/ unpolarized electronsSpin statisticselectron gas in Magnetic FieldFerromagnetic metalsSpin TorqueSpin-Torque CurrentSpin-Transfer TorqueQuantum Nature of SpinQuestions & Answers
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionScatteringsSpin-polarized/ unpolarized electronsSpin statisticselectron gas in Magnetic FieldFerromagnetic metalsSpin TorqueSpin-Torque CurrentSpin-Transfer TorqueQuantum Nature of SpinQuestions & Answers
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
|
Spin-Orbit Interaction
Spin and Charge TransportSpin-orbit interaction refers to a magnetic field of relativistic origin experienced by an electron while moving within an electric field.The spin-orbit interaction stands as one of the most crucial fundamental effects in physics, holding a pivotal role in numerous phenomena within Solid State Physics.
|
Spin-orbit interaction describes the generation of a magnetic field resulting from the movement of an electron in an electric field. |
|
Despite its relativistic origin, the magnetic field of the spin-orbit interaction is just as real as any other existing magnetic field. |
(fact) The spin-orbit interaction that arises from the electric field of the nucleus and the orbital motion of the electron is widely recognized as the most prominent, influential, and robust form of spin-orbit interaction.Magnetic anisotropy, perpendicular magnetic anisotropy (PMA), voltage- controlled magnetic anisotropy (VCMA), g- factor, spin Hall effect, Anomalous Hall effect (AHE) , Anomalous Magneto Resistance (AMR) and many other effects are due to this type of the spin orbit - interaction. |
When an external magnetic field is applied to an electron orbital, it generates an additional magnetic field due to the spin-orbit interaction. Consequently, the electron spin interacts with a composite magnetic field that is larger than the externally applied one.(see details here). |
|
| Magnetic anisotropy is due to this effect. See Perpendicular magnetic anisotropy |
| Measurement of the strength of spin- orbit interaction is based on this effect (See below) |
![]()

Relativistic origin of the Spin-Orbit Interaction |
 |
| Fig.3 An object (e.g., an electron) depicted in red is in motion within a static electric field. In the coordinate system moving alongside the object, the static electric field undergoes relativistic transformation, resulting in the emergence of an effective electric field Eeff and an effective magnetic field Heff . If the particle possesses a magnetic moment (spin), spin precession occurs around the effective magnetic field Heff. and spin is aligned along Heff. |
| The effective magnetic field Heff. is referred to as the magnetic field of the spin-orbit interaction Hso., serving as the sole parameter that characterizes this interaction. |
According to the Theory of Relativity, the electric and magnetic fields are interconverted depending on the observer's velocity. For instance, if a static observer's coordinate system contains only a magnetic field, a moving observer will perceive this field as both an electric and a magnetic field.
When a particle moves within a static magnetic field, it encounters an effective electric field. This field influences the particle's charge (manifesting as the Lorentz force or Hall effect) and drives the particle along its direction.
Conversely, when a particle moves within a static electric field, it encounters an effective magnetic field, which is called the magnetic field Hso of spin- orbit interaction.. This field acts on the particle's magnetic moment (particle's spin), inducing precession of the magnetic moment around the effective magnetic field's direction, which eventually aligns the spin along Hso.
Hall effect ====movement in magnetic field====results in ====> effective electrical field
Spin-Orbit interaction =======movement in magnetic field====results in=====> effective magnetic field
The electromagnet field is a relativistic object and it is the Lorentz transformation rules as
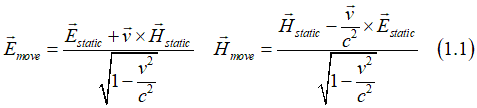
where Estatic, Hstatic are the electric and magnetic field in the static coordinate system (reference frame) and Emove, Hmove are the electric and magnetic field in the coordinate system, which moves with a constant speed v.
As a result, an electron, which moves in a static magnetic field Hstatic, experience in own reference frame an effective electrical field EHall , which is called the Hall field (Hall voltage). Similarly, when an electron moves in a static electrical field Estatic, it experience in own reference frame an effective magnetic field HSO , which is called the effective spin-orbit magnetic field
For example, when an electron moves in the x-direction
![]()
in
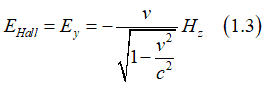
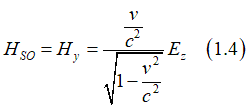
| The Lorentz force is a tween effect with the effect of the spin-orbit interaction | ||||
|
in this case 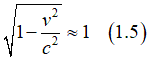 and
and
The Hall field can be calculated as
![]()
The spin-orbit magnetic field can be calculated as
The trajectory of an electron can vary significantly. There are numerous scenarios where an electron moves perpendicular to an electric field. All that's necessary is for the electron to initially possess a velocity component perpendicular to the electric field. This occurs, for instance, when the electron orbits around a nucleus.
![]()
 (reason why): It is because the effect of spin- orbit interaction describes the magnetic field of a relativistic origin, which manifests itself when an electron moves in an electrical field. Despite the complexity of various configurations involving spin- orbit interaction, this magnetic field serves as the sole parameter characterizing the spin-orbit interaction.
(reason why): It is because the effect of spin- orbit interaction describes the magnetic field of a relativistic origin, which manifests itself when an electron moves in an electrical field. Despite the complexity of various configurations involving spin- orbit interaction, this magnetic field serves as the sole parameter characterizing the spin-orbit interaction.
Spin-orbit interaction describes the generation of a magnetic field resulting from the movement of an electron in an electric field. |
|
Despite its relativistic origin, the magnetic field of the spin-orbit interaction is just as real as any other existing magnetic field. |
![]() (fact): Spin-orbit interaction persists even in the absence of an orbital moment.
(fact): Spin-orbit interaction persists even in the absence of an orbital moment.
(It is important): There is a singular parameter that encapsulates the essence of spin-orbit interaction: the magnetic field Hso. All other aspects of this interaction are derived from Hso. For instance, when Hso interacts with electron spin, it aligns the spin along its direction. The energy associated with this interaction, denoted as Eso, is a consequence rather than a primary parameter of spin-orbit interaction. When an external magnetic field Hext is introduced, the electron spin aligns itself with the total magnetic field Hso + Hext , and the resulting magnetic energy is determined by the total magnetic field, where Eso lacks exclusive physical significance. Thus, Hso stands as the sole parameter that fully characterizes and delineates the nature of spin-orbit interaction.
![]()
![]()
![]()
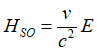
![]()
![]()
![]()
Indeed, the proportionality to 1/c2 renders Hso relatively small. However, when the electric field Estatic is substantial and the electron's velocity approaches the speed of light c, Hso can become moderate or even large. This scenario occurs, for instance, when an electron orbits around a nucleus. In such proximity, the electric field of the nucleus intensifies inversely with the distance to the nucleus (1/r). Since the nucleus behaves nearly as a point-like object , the electric field Estatic is exceedingly large nearby (r~0). Consequently, Hso amplifies significantly under these conditions.
The magnetic field Hso of spin- orbit interaction is just as real as any other magnetic field. However, its unique characteristic lies in its local nature. In conventional global magnetic fields, all objects placed at the same local point experience the same magnetic field regardless of their nature. In contrast, the magnetic field of spin-orbit interaction varies significantly for each individual orbital. This local variability is a clear experimental fact, ,where neighboring orbitals near an interface can experience orders of magnitude difference in Hso. Remarkably, even two orbitals from the same nucleus can exhibit substantially different Hso values.
![]() (Decisive role 1) Family of magneto- transport effects.
(Decisive role 1) Family of magneto- transport effects.
![]() This unique locality of the magnetic field Hso of spin- orbit interaction plays a key role in the origins of numerous magneto-transport phenomena, such as the Spin Hall effect and Anomalous Hall effect, etc. This locality of Hso plays a decisive role in making electron scattering spin-dependent. When an electron is scattered to a nearby or the same point but a different quantum state, it encounters a distinct Hso. Consequently, the magnetic energy of the electron's final state varies with the direction of its spin, leading to a difference of scattering probabilities based on the spin direction of the scattered electron. This spin-preferential scattering results in spin accumulation. Consequently, electron currents generate spin accumulation and the properties of the electron current become spin- dependent. The diverse manifestations of this effect give rise to a spectrum of magneto-transport phenomena.
This unique locality of the magnetic field Hso of spin- orbit interaction plays a key role in the origins of numerous magneto-transport phenomena, such as the Spin Hall effect and Anomalous Hall effect, etc. This locality of Hso plays a decisive role in making electron scattering spin-dependent. When an electron is scattered to a nearby or the same point but a different quantum state, it encounters a distinct Hso. Consequently, the magnetic energy of the electron's final state varies with the direction of its spin, leading to a difference of scattering probabilities based on the spin direction of the scattered electron. This spin-preferential scattering results in spin accumulation. Consequently, electron currents generate spin accumulation and the properties of the electron current become spin- dependent. The diverse manifestations of this effect give rise to a spectrum of magneto-transport phenomena.
![]() (Decisive role 2) Perpendicular magnetic anisotropy (PMA)
(Decisive role 2) Perpendicular magnetic anisotropy (PMA)
 Electrons at the interface experience an order of magnitude larger strength of spin-orbit interaction compared to their close neighbors in the bulk. This heightened spin-orbit interaction leads to perpendicular magnetic anisotropy (PMA), where the magnetization of a nanomagnet aligns perpendicularly to the interface. Due to this strong spin-orbit interaction, a significant amount of magnetic energy is concentrated at the interface.
Electrons at the interface experience an order of magnitude larger strength of spin-orbit interaction compared to their close neighbors in the bulk. This heightened spin-orbit interaction leads to perpendicular magnetic anisotropy (PMA), where the magnetization of a nanomagnet aligns perpendicularly to the interface. Due to this strong spin-orbit interaction, a significant amount of magnetic energy is concentrated at the interface.
This concentration of magnetic energy ensures that even small nanomagnets retain a considerable amount of magnetic energy, making them resistant against information loss due to unwanted thermal fluctuations. This property enables the storage of information in extremely small nanomagnets, facilitating the development of highly dense magnetic recording technologies such as those used in hard disks.

![]()
![]()
![]() (global magnetic field): The global magnetic field is the conventional magnetic field produced, for example, by a permanent magnet. All objects experience an equal amount of the magnetic field, when they are inside the global magnetic field.
(global magnetic field): The global magnetic field is the conventional magnetic field produced, for example, by a permanent magnet. All objects experience an equal amount of the magnetic field, when they are inside the global magnetic field.
 The spatial distribution of the global magnetic field changes gradually and uniformly over space. Consequently, during electron scatterings, the magnetic field experienced by the electron remains consistent and does not vary significantly. Consequently, electron scatterings within this field remain independent of spin orientation.
The spatial distribution of the global magnetic field changes gradually and uniformly over space. Consequently, during electron scatterings, the magnetic field experienced by the electron remains consistent and does not vary significantly. Consequently, electron scatterings within this field remain independent of spin orientation.
![]()
![]()
![]() (local magnetic field): The locality is a unique feature of the magnetic field of spin- orbit interaction. This field can vary significantly in magnitude between closely neighboring electron orbitals, sometimes differing by orders of magnitude. Furthermore, even electrons occupying distinct orbitals of the same nucleus can encounter vastly different magnetic fields due to spin-orbit interaction.
(local magnetic field): The locality is a unique feature of the magnetic field of spin- orbit interaction. This field can vary significantly in magnitude between closely neighboring electron orbitals, sometimes differing by orders of magnitude. Furthermore, even electrons occupying distinct orbitals of the same nucleus can encounter vastly different magnetic fields due to spin-orbit interaction.
|
 Due to the local nature of the magnetic field of spin-orbit interaction, its magnitude varies significantly when an electron undergoes scattering from one quantum state to another. Consequently, the scattering probability differs based on the electron's spin direction. This spin-dependent scattering gives rise to a range of magneto-transport phenomena, including the Spin Hall Effect, Anomalous Hall Effect (AHE), and AMR/PHE effect, among others.
Due to the local nature of the magnetic field of spin-orbit interaction, its magnitude varies significantly when an electron undergoes scattering from one quantum state to another. Consequently, the scattering probability differs based on the electron's spin direction. This spin-dependent scattering gives rise to a range of magneto-transport phenomena, including the Spin Hall Effect, Anomalous Hall Effect (AHE), and AMR/PHE effect, among others.
 Electric field of a nucleus is only an electrical field creating a sizable spin- orbit interaction.
Electric field of a nucleus is only an electrical field creating a sizable spin- orbit interaction.  Orbital movement around a nucleus is only an electron movement generating a sizable spin- orbit interaction.
Orbital movement around a nucleus is only an electron movement generating a sizable spin- orbit interaction.All significant effects arising from spin-orbit interaction are attributed to the orbital movements of electrons and the electric field of a nucleus. Examples of such substantial effects include magnetization alignment in a magnet, magnetic anisotropy, fine orbital structure, spin-dependent scatterings, the Spin Hall effect, and nearly all magneto-transport effects.
|
| Only the electric field of a nucleus is responsible for creating a significant spin-orbit interaction. Similarly, only orbital movement around a nucleus generates a sizable spin-orbit interaction. |
| Other sources of an electric field, such as an externally applied electric field, and non-orbital electron movement may also give rise to spin-orbit interaction. However, this type of spin-orbit interaction is minuscule and typically only observable at near-zero temperatures |
 (why is SO small in general?): Except the orbital movement, the spin- orbit interaction is very weak as the formula for the magnetic field of spin-orbit interaction has the speed of light squared in the denominator:
(why is SO small in general?): Except the orbital movement, the spin- orbit interaction is very weak as the formula for the magnetic field of spin-orbit interaction has the speed of light squared in the denominator:

However, it becomes substantial when an electron orbits a nucleus, mainly due to two factors ![]() :
:
 (1st factor why SO is large for orbital movement): Electric field near the nucleus is extremely strong.
(1st factor why SO is large for orbital movement): Electric field near the nucleus is extremely strong.
 (2nd factor why SO is large for orbital movement): Electron orbits at an exceedingly high, near-relativistic speed. For instance, the speed of an electron in the first orbital of a hydrogen atom is 1/137th of the speed of light, indicating very fast movement.
(2nd factor why SO is large for orbital movement): Electron orbits at an exceedingly high, near-relativistic speed. For instance, the speed of an electron in the first orbital of a hydrogen atom is 1/137th of the speed of light, indicating very fast movement.
![]() If a sizable spin-orbit interaction can only be created by the electric field of the nucleus, then how can a gate voltage of only 1 V substantially modulate the strength of the spin-orbit interaction (VCMA effect)?
If a sizable spin-orbit interaction can only be created by the electric field of the nucleus, then how can a gate voltage of only 1 V substantially modulate the strength of the spin-orbit interaction (VCMA effect)?
It's important to note that the gate electrical field itself does not generate the spin-orbit interaction. Rather, it modulates the existing spin-orbit interaction generated by the electric field of the nucleus. The influence of the gate voltage on the spin-orbit interaction is indirect rather than direct.
The spin-orbit interaction, which is generated by the nucleus, comprises two nearly equal but opposite components corresponding to the clockwise and counterclockwise orbital rotations of the electron around the nucleus. These two large components almost cancel each other out, and only a small difference between them defines the overall spin-orbit interaction experienced by the electron.
When a gate voltage is applied, it modifies the orbital distribution of electrons at the interface. This change alters the difference between the two opposite contributions to the spin-orbit interaction, effectively modulating its overall strength. In this scenario, the spin-orbit interaction is initially generated by the electric field of the nucleus and then further influenced or modulated by the gate voltage.
![]() If a significant spin-orbit interaction can only be generated due to the orbital rotation of the electron around the nucleus, then how can a moderate electron current of only 50 mA/um² substantially modulate the strength of the spin-orbit interaction (SOT effect)? After all, the electron current only slightly changes the flow speed of electrons, yet it has a profound effect.
If a significant spin-orbit interaction can only be generated due to the orbital rotation of the electron around the nucleus, then how can a moderate electron current of only 50 mA/um² substantially modulate the strength of the spin-orbit interaction (SOT effect)? After all, the electron current only slightly changes the flow speed of electrons, yet it has a profound effect.
The influence of the electron current on the strength of the spin-orbit interaction is not merely due to changes in electron speed which results in variation in spin-orbit interaction strength. Instead, its impact is more intricate and indirect.
The spin-orbit interaction makes electron scattering spin-dependent. However, in the absence of an electron current, the spin-dependent scatterings balance each other out for any two opposite directions of spin, resulting in no spin effect. When there is an electrical current, it disrupts this balance. The scattering of electrons with one spin direction becomes more frequent than the scatterings of electrons with the opposite spin directions. This leads to spin-dependent resistance and spin accumulation, which in turn result in various magneto-transport effects.
In summary, while the electron current does not directly change the strength of the spin-orbit interaction, which is generated by the orbital movement, its influence on spin-dependent scatterings leads to spin accumulation, which underpins the substantial modulation of the spin-orbit interaction strength.
 Confusing meaning of the historical name "spin-orbit interaction"
Confusing meaning of the historical name "spin-orbit interaction" The spin-orbit interaction is not directly associated with the spin or the orbital momentum, nor is it an interaction between them. Instead, it primarily describes the magnetic field Hso of relativistic origin. This magnetic field is the sole parameter characterizing the spin-orbit interaction.
The spin-orbit interaction is not directly associated with spin or orbital momentum or interaction between them. |
| The primary and sole parameter described by the spin-orbit interaction is the magnetic field Hso . In certain scenarios, but not universally, Hso aligns with the orbital momentum, while the spin aligns with Hso, indirectly influencing the alignment of the spin with the orbital momentum. However, this alignment is not a universal rule and applies only in specific cases. |
| click on image to enlarge it |
 The name "Spin-orbit interaction" is historical but somewhat misleading, as it does not accurately represent the true nature of the effect.
The name "Spin-orbit interaction" is historical but somewhat misleading, as it does not accurately represent the true nature of the effect.

![]() (distant relation with the spin): The only parameter of an electron with which the magnetic field of spin-orbit interaction interacts is the spin. Due to its relativistic nature, this magnetic field does not interact with the magnetic moment arising from the orbital moment. Therefore, the inclusion of "spin" in the name might be partially justified.
(distant relation with the spin): The only parameter of an electron with which the magnetic field of spin-orbit interaction interacts is the spin. Due to its relativistic nature, this magnetic field does not interact with the magnetic moment arising from the orbital moment. Therefore, the inclusion of "spin" in the name might be partially justified.

![]() (distant relation with the orbital moment): The relationship with the orbital moment is intricate. The presence of spin-orbit interaction requires the breaking of time-inverse symmetry or T- symmetry in short.. An electron orbital, when T-symmetry is broken, typically possesses a non-zero orbital moment. Therefore, spin-orbit interaction has an indirect connection with the orbital moment. Typically, the existence of an orbital moment implies the presence of spin-orbit interaction. However, this complex relationship can sometimes be disrupted. For instance, the most robust spin-orbit interaction is found in a ferromagnetic metal, despite the localized electrons within it typically having a quenched orbital moment, meaning orbital moment is zero.
(distant relation with the orbital moment): The relationship with the orbital moment is intricate. The presence of spin-orbit interaction requires the breaking of time-inverse symmetry or T- symmetry in short.. An electron orbital, when T-symmetry is broken, typically possesses a non-zero orbital moment. Therefore, spin-orbit interaction has an indirect connection with the orbital moment. Typically, the existence of an orbital moment implies the presence of spin-orbit interaction. However, this complex relationship can sometimes be disrupted. For instance, the most robust spin-orbit interaction is found in a ferromagnetic metal, despite the localized electrons within it typically having a quenched orbital moment, meaning orbital moment is zero.

![]() (important example 1):
(important example 1): ![]() (when spin- orbit interaction is not related to interaction between orbital momentum and spin):
(when spin- orbit interaction is not related to interaction between orbital momentum and spin):
Existence of a strong spin- orbit interaction in absence of the orbital moment.
In a solid, the localized electrons at an interface experience the strongest spin-orbit interaction, as evidenced by the the perpendicular magnetic anisotropy (PMA) phenomenon. However, the orbital moment of these localized electrons is fully quenched, meaning their orbital moment is effectively zero.
![]() (important example 2):
(important example 2): ![]() (when spin- orbit interaction is not related to interaction between orbital momentum and spin):
(when spin- orbit interaction is not related to interaction between orbital momentum and spin):
(experimental fact) Linear Dependence of strength of spin- orbit interaction on external magnetic field
The external magnetic field enhances the strength of spin-orbit interaction, as evidenced by the experimentally measured increase in the anisotropy field under the external magnetic field. This enhancement occurs because the existence of magnetic anisotropy is defined by spin-orbit interaction. Consequently, the strength of magnetic anisotropy is proportional to the strength of spin-orbit interaction.
![]() (Why is "spin" used in the name "spin- orbit interaction"?)
(Why is "spin" used in the name "spin- orbit interaction"?)
The only property of an electron with which the magnetic field of the spin-orbit interaction, HSO, can interact is the electron spin. The magnetic field HSO of the spin-orbit interaction does not interact with the electron's orbital moment. The electron spin is the sole remaining magnetic property of an electron that can interact with HSO.
![]() (Why is "orbit" used in the name "spin- orbit interaction"?)
(Why is "orbit" used in the name "spin- orbit interaction"?)
The primary and sole parameter described by the spin-orbit interaction is the magnetic field HSO. The orbital moment describes the degree of the broken rotational symmetry of the electron orbital. The direction of the magnetic field HSO of the spin-orbit interaction is aligned along the direction of the broken T-symmetry. Since the rotational symmetry encompasses the T-symmetry, in certain scenarios—though not universally— HSO aligns with the orbital momentum.
 Math Origin of spin-orbit interaction: the Lorentz transformation or the Dirac equation?
Math Origin of spin-orbit interaction: the Lorentz transformation or the Dirac equation?
|
Both the Lorentz transformation and the Dirac equation provide equivalent and analogous descriptions of the spin-orbit interaction. |
| The difference between these two equivalent descriptions lies in the reference frame (moving system coordinate) in which the interaction between a moving electron and a static electric field is described. |
| click on image to enlarge it |
![]() (fact): Both the Lorentz transformation and the Dirac equation provide equivalent and analogous descriptions of the spin-orbit interaction.
(fact): Both the Lorentz transformation and the Dirac equation provide equivalent and analogous descriptions of the spin-orbit interaction.
The spin-orbit interaction is a consequence of the electromagnetic field's invariance under relativistic transformations, also known as Lorentz transformations. Analogous to the electromagnetic field, the quantum field of electrons maintains its invariance under relativistic changes, a property encapsulated by the Dirac equation. Remarkably, the Dirac equation yields the exact same equation (Eq.1.7).
(The Lorentz transformation): describes how the same distribution of electric and magnetic fields appears in different moving system coordinates.
(The Dirac equation): describes how the same distribution of quantum field of an electron (wavefunction) and its interaction with the electromagnetic field appear in different moving system coordinates.
![]() (reason why Lorentz transformation and the Dirac equation yield exactly the same effect of spin- orbit interaction): This equivalence arises from the following reason: The spin-orbit interaction (SO) characterizes the interaction of a moving electron with an electric field, a phenomenon that remains consistent regardless of the chosen coordinates for calculation. It is possible to carry out calculations in a coordinate system that moves with the electron. Consequently, the electromagnetic field necessitates relativistic transformation. Similarly, computations conducted in the steady coordinate of the electric field can yield the same outcome for HSO. In this scenario, the quantum field requires a relativistic transformation, leading to the deduction of SO from the Dirac Equation.
(reason why Lorentz transformation and the Dirac equation yield exactly the same effect of spin- orbit interaction): This equivalence arises from the following reason: The spin-orbit interaction (SO) characterizes the interaction of a moving electron with an electric field, a phenomenon that remains consistent regardless of the chosen coordinates for calculation. It is possible to carry out calculations in a coordinate system that moves with the electron. Consequently, the electromagnetic field necessitates relativistic transformation. Similarly, computations conducted in the steady coordinate of the electric field can yield the same outcome for HSO. In this scenario, the quantum field requires a relativistic transformation, leading to the deduction of SO from the Dirac Equation.
Spin-orbit interaction in macro world |
 |
| Fig. 5. An imaginary case what would happen if the Sun were charged. In this case the magnetic moment of the Earth would be aligned in respect to the polarity of the Sun charge. The red arrow shows direction of the magnetic moment of the Earth. The blue arrow shows the direction of the effective magnetic field HSO due to the effect of the spin-orbit interaction, which is induced by the electrical field due to the Sun charge. When the the polarity of the charge is reversed, the direction of the effective magnetic field is reversed as well. It follows by the precession of the magnetic moment of the Earth around the effective field until it aligns itself to be antiparallel in respect to the SO magnetic field HSO. |
A. No, the Spin-Orbit interaction doesn't just impact small objects; it also influences large-scale phenomena in the macro world.
For example, Figure 5 shows an imaginary case of what would happen if the Sun were charged. In this hypothetical case, the magnetic moment of the Earth would interact with the effective magnetic field HSO resulting from the spin-orbital interaction induced by this charge. As illustrated in Fig.5, the magnetic moment of the Earth would align accordingly due to this interaction.
A. No, that statement is not entirely correct. The spin-orbit interaction is indeed a relativistic effect, originating from the relativistic corrections to the classical electromagnetic theory, particularly the magnetic field. While it's true that the spin-orbit interaction can be derived from the relativistic Dirac equations, it is not solely a quantum mechanical effect. However, many quantum mechanical phenomena do incorporate aspects of the spin-orbit interaction due to its fundamental role in describing the behavior of particles with intrinsic spin.
![]() facts about relativistic nature of spin- orbit interaction in short:
facts about relativistic nature of spin- orbit interaction in short:
(1) The spin-orbit interaction is indeed a relativistic effect and can be accurately described by relativistic equations.
(2) The Dirac equation is a relativistic quantum-mechanical equation that accounts for the relativistic transformation of both the electromagnetic field and the quantum field of an electron. Calculations of the spin-orbit interaction using the Dirac equation yield highly precise results due to its relativistic nature. (Refer to "SO and Dirac equation" for details.)
(3) The Schrödinger equation (no spin) and the Pauli equation (simple spin) are also able to describe the spin-orbit interaction, although they do not explicitly account for the relativistic transformation of the quantum field of an electron. However, by introducing corrected constants and parameters, it is possible to modify these equations to accurately describe the spin-orbit interaction, achieving results that are fully consistent with those obtained from the Dirac equation.

 Critical importance of breaking of time- inverse symmetry (T- symmetry) for existence of spin- orbit interaction
Critical importance of breaking of time- inverse symmetry (T- symmetry) for existence of spin- orbit interaction 

(important fact) The spin-orbit interaction only manifests itself when the time-reversal symmetry (T-symmetry) is broken by an external source.
(important fact) The spin-orbit interaction itself cannot break the T-symmetry. An external source is always required to break the T-symmetry for an object, thereby enabling the spin-orbit interaction to influence the object.
Sizable spin-orbit interaction occurs exclusively during the orbital motion of an electron around a nucleus. The orbital movement of electron can be divided into two equal components, where the electron moves either clockwise or counterclockwise.
When T-symmetry remains unbroken for the orbital movement, the directions of the magnetic fields generated by the spin-orbit interaction for the clockwise and counterclockwise movements are opposite. As a result, these two contributions balance each other out, leading to no net spin-orbit interaction experienced by the electron. In this scenario, the unbroken T-symmetry implies that reversing the flow direction of time results in an exchange between clockwise and counterclockwise movement paths, which does not alter anything.
For spin-orbit interaction to exist,, T-symmetry must be broken, creating a distinction between clockwise and counterclockwise rotations. This symmetry is externally broken by the application of a magnetic field, which induces the Lorentz force. This force acts differently on the electron along its clockwise and counterclockwise paths.
Specifically, the Lorentz force pushes the clockwise-rotating part of the electron wavefunction away from the nucleus, while simultaneously drawing the counterclockwise-rotating part closer to it. This creates a disparity in the electric field experienced by the two rotations. Consequently, the equilibrium between opposing magnetic fields of spin-orbit interaction is disrupted, leading to a significant magnetic field experienced by the electron.
![]() Is the existence of the Lorentz force induced by the external magnetic field a critical requirement for the spin-orbit interaction to occur?
Is the existence of the Lorentz force induced by the external magnetic field a critical requirement for the spin-orbit interaction to occur?
![]() (2024.04) No, the critical condition for the existence of spin-orbit interaction lies in the disparity between the clockwise-rotating and counterclockwise-rotating parts of the electron wavefunction. This disparity can arise from various sources, including the Lorentz force induced by an external magnetic field, an electrical current, or the presence of an unquenched orbital moment in the electron.
(2024.04) No, the critical condition for the existence of spin-orbit interaction lies in the disparity between the clockwise-rotating and counterclockwise-rotating parts of the electron wavefunction. This disparity can arise from various sources, including the Lorentz force induced by an external magnetic field, an electrical current, or the presence of an unquenched orbital moment in the electron.
Essential Role of Broken Time-Reversal Symmetry in Spin-Orbit Interaction |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||
| click on image to enlarge it |
Spin-orbit interaction only manifests itself when T-symmetry is broken by an external source. Three distinct methods exist to break T-symmetry, each defining a unique type of spin-orbit interaction.
| 3 distinct types of spin-orbit interaction |
|---|
 |
| Three distinct methods exist to break T-symmetry, each defining a unique type of spin-orbit interaction. While all 3 effects are rooted in spin-orbit interaction, they represent different manifestations and should be treated as separate |
| click on image to enlarge it |
![]() (1st type of spin- orbit interaction): The first type of spin-orbit interaction arises when there is an unquenched orbital moment, commonly observed in conduction electrons and orbital electrons within atomic gases.
(1st type of spin- orbit interaction): The first type of spin-orbit interaction arises when there is an unquenched orbital moment, commonly observed in conduction electrons and orbital electrons within atomic gases.
(how it manifests itself): This type of spin-orbit interaction manifests itself in varying energies for the light-hole, heavy-hole, and split-off bands of valence electrons in a semiconductor.
![]() (how T-symmetry is broken): Due to a non-zero orbital moment.
(how T-symmetry is broken): Due to a non-zero orbital moment.
![]() (2nd type of spin- orbit interaction): The second method of breaking T-symmetry involves the application of an external magnetic field. This type of spin-orbit interaction is induced by an external magnetic field and exhibits a linear relationship with the externally applied magnetic field.
(2nd type of spin- orbit interaction): The second method of breaking T-symmetry involves the application of an external magnetic field. This type of spin-orbit interaction is induced by an external magnetic field and exhibits a linear relationship with the externally applied magnetic field.
(how it manifests itself): This type of spin-orbit interaction is responsible for magnetization alignment in a magnet and magnetic anisotropy.
![]() (how T-symmetry is broken): Due to an external magnetic field.
(how T-symmetry is broken): Due to an external magnetic field.
![]() (3rd type of spin- orbit interaction): The third type of spin-orbit interaction emerges in the presence of an electrical current, which breaks the T-symmetry. This type of spin-orbit interaction leads to a dependency of scattering probabilities of conduction electrons on their spin direction.
(3rd type of spin- orbit interaction): The third type of spin-orbit interaction emerges in the presence of an electrical current, which breaks the T-symmetry. This type of spin-orbit interaction leads to a dependency of scattering probabilities of conduction electrons on their spin direction.
(how it manifests itself): This type of spin-orbit interaction (SO) makes electron scattering spin-dependent, leading to spin-dependent electron transport. As a result, electron transport becomes sensitive to spin orientation, giving rise to spin-dependent transport phenomena such as the Spin Hall effect, the Anomalous Hall effect, etc (see here).
![]() (how T-symmetry is broken): Due to an electron current
(how T-symmetry is broken): Due to an electron current
![]() Can you compare the strength of spin- orbit interaction measured from strength of magnetic anisotropy and from magneto- transport effects?
Can you compare the strength of spin- orbit interaction measured from strength of magnetic anisotropy and from magneto- transport effects?
![]() (2024.04) No, it is not possible to directly compare the strength of spin-orbit interaction measured from the strength of magnetic anisotropy and from magneto-transport effects. These are fundamentally different phenomena with distinct properties, constants, characteristics, and underlying mechanisms. While both effects are rooted in spin-orbit interaction, they represent different manifestations and should be treated as separate phenomena.
(2024.04) No, it is not possible to directly compare the strength of spin-orbit interaction measured from the strength of magnetic anisotropy and from magneto-transport effects. These are fundamentally different phenomena with distinct properties, constants, characteristics, and underlying mechanisms. While both effects are rooted in spin-orbit interaction, they represent different manifestations and should be treated as separate phenomena.
 Video: Spin-orbit interaction. Fundumentals. Video: Spin-orbit interaction. Fundumentals. |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||
| click on image to watch on YouTube |

![]() Why and how time- inverse symmetry (T- symmetry) is broken for unquenched electrons?
Why and how time- inverse symmetry (T- symmetry) is broken for unquenched electrons?
 (quenched electrons): In the case of a quenched electron, whose orbital moment is zero, the orbital motion can be divided into clockwise and counterclockwise paths around a nucleus. During rotation along each path, the electron experiences an equal but opposite magnetic field of spin-orbit interaction. Consequently, the net effect is that the electron experiences no spin-orbit interaction.
(quenched electrons): In the case of a quenched electron, whose orbital moment is zero, the orbital motion can be divided into clockwise and counterclockwise paths around a nucleus. During rotation along each path, the electron experiences an equal but opposite magnetic field of spin-orbit interaction. Consequently, the net effect is that the electron experiences no spin-orbit interaction.
![]() The key factor for the absence of spin-orbit interaction in this scenario is not solely the zero orbital moment but rather the unbroken T-symmetry. However, the absence of an orbital moment can indeed be linked to the lack of spin-orbit interaction.
The key factor for the absence of spin-orbit interaction in this scenario is not solely the zero orbital moment but rather the unbroken T-symmetry. However, the absence of an orbital moment can indeed be linked to the lack of spin-orbit interaction.
 (breaking T-symmetry): The orbital motion of an electron possessing a non-zero orbital momentum can be represented as a single path with a specific rotation direction. The absence of opposing contributions results in the electron experiencing the magnetic field of spin-orbit interaction solely in one direction, which is aligned with the orientation of the orbital moment. Once again, the crucial determinant in this scenario is the direction of the broken T-symmetry, defining both the orientation of the orbital momentum and the magnetic field of spin-orbit interaction.
(breaking T-symmetry): The orbital motion of an electron possessing a non-zero orbital momentum can be represented as a single path with a specific rotation direction. The absence of opposing contributions results in the electron experiencing the magnetic field of spin-orbit interaction solely in one direction, which is aligned with the orientation of the orbital moment. Once again, the crucial determinant in this scenario is the direction of the broken T-symmetry, defining both the orientation of the orbital momentum and the magnetic field of spin-orbit interaction.
The g-factor describes the ratio between the spin or the orbital moment and the magnetic moment of an electron

where S is ether the electron spin S or the electron orbital momentum L or electron total moment J
![]() (fact 1): The g-factor is equal to 2 for an electron that possesses spin but lacks an orbital momentum.
(fact 1): The g-factor is equal to 2 for an electron that possesses spin but lacks an orbital momentum.
![]() (fact 2): The g-factor is equal to 1 for an electron that has orbital momentum but no spin.
(fact 2): The g-factor is equal to 1 for an electron that has orbital momentum but no spin.
------------------------------
 (it is important): The value of the g-factor varies across different materials. It is a crucial parameter that characterizes the magnetic and spin properties of electrons.
(it is important): The value of the g-factor varies across different materials. It is a crucial parameter that characterizes the magnetic and spin properties of electrons.
-------------------
 |
|---|
| This difference arises from the distinct ways each type of symmetry generates a magnetic moment from a given electric charge and broken T-symmetry. |
 (reason 1): Different contributions to the magnetic moment arise from contributions of distinct symmetries described by spin and orbital momentum. This variation results in the g-factor ranging from 1 (for orbital momentum only) to 2 (for spin only).
(reason 1): Different contributions to the magnetic moment arise from contributions of distinct symmetries described by spin and orbital momentum. This variation results in the g-factor ranging from 1 (for orbital momentum only) to 2 (for spin only).
The existence of a magnetic moment requires the breaking of T-symmetry. There are two symmetries, each including within itself the T-symmetry and each contributing to the magnetic moment. The spin describes specifically the breaking of T- symmetry only, while orbital momentum breaks a more complex rotational symmetry that includes T-symmetry.
Due to the fundamental differences in the symmetries described by spin and orbital momentum, their contributions to the magnetic moment differ significantly. The magnetic moment due to spin is twice as large as the magnetic moment due to orbital momentum.
 (reason 2): Additional Contribution from the Magnetic Field of Spin-Orbit Interaction
(reason 2): Additional Contribution from the Magnetic Field of Spin-Orbit Interaction
Due to spin-orbit interaction, the external magnetic field induces an additional magnetic field known as the magnetic field of spin- orbit interaction.. Consequently, the energy splitting becomes proportional to the sum of the applied magnetic field and the magnetic field of spin- orbit interaction. This results in a larger Zeeman splitting and, therefore, a larger g-factor.
![]() The g-factor defines the ratio between the magnetic moment and the spin and/or orbital momentum. Why does the additional magnetic field matter?
The g-factor defines the ratio between the magnetic moment and the spin and/or orbital momentum. Why does the additional magnetic field matter?
(answer): It is because of the method of how the g-factor is measured.
(reason why additional magnetic field affects g- factor): The magnetic moment of an electron is determined from its magnetic properties, particularly through Zeeman splitting. When subjected to a magnetic field, the electron level splits into two sublevels, corresponding to the magnetic moment aligned parallel and antiparallel to the field. The energy splitting is linearly proportional to the applied magnetic field. When an additional magnetic field, proportional to the external magnetic field, is present, the actual applied magnetic field becomes larger for a given external magnetic field. Consequently, the energy splitting increases. This increase in energy splitting is reflected in (described by) an enlarged g-factor.
![]() Why don’t we define the values of spin or orbital momentum so that they contribute equally to the magnetic moment? This would eliminate the complexity associated with the g-factor.
Why don’t we define the values of spin or orbital momentum so that they contribute equally to the magnetic moment? This would eliminate the complexity associated with the g-factor.
The reason lies in the conservation of T-symmetry. It is impossible to assign different values to spin and orbital moments due to the necessity of conserving T-symmetry. For example, during the transfer of spin from a photon to an electron’s spin or orbital moment, both the electron spin and orbital moment must correspond to the photon spin.
![]() Is the magnetic moment a conserved parameter? How does the conservation of the magnetic moment differ from T-symmetry conservation?
Is the magnetic moment a conserved parameter? How does the conservation of the magnetic moment differ from T-symmetry conservation?
The magnetic moment is not a conserved parameter, whereas T-symmetry is always conserved. For example, a circularly polarized photon does not have a magnetic moment. When it is absorbed by an electron, a larger magnetic moment is created if the photon's spin is transferred to the electron's spin. A smaller magnetic moment is created if the photon's spin is transferred to the electron's orbital momentum. The path of transformation of the photon's spin is governed by the law of T-symmetry conservation.
----------------------
 |
|---|
Similar to how electric and magnetic fields are complementary components of a single electromagnetic field, the magnetic moment and electric charge are two complementary components of one quantity of an elementary particle. The electric and magnetic fields transform into each other under the relativistic transformations and are connected through the broken T-symmetry. A similar relationship exists between electric charge and magnetic moment.
![]()
![]() (existence of a magnetic moment): Two conditions are required for the existence of a magnetic moment in an elementary particle: the particle must possess an electric charge, and its T-symmetry must be broken.
(existence of a magnetic moment): Two conditions are required for the existence of a magnetic moment in an elementary particle: the particle must possess an electric charge, and its T-symmetry must be broken.
![]()
![]() (when T-symmetry is broken): (1) particle has a spin; or/and (2) particle has an orbital moment
(when T-symmetry is broken): (1) particle has a spin; or/and (2) particle has an orbital moment
--------
![]()
![]() (case 1, when there is no magnetic moment): there is no electric charge: Photon
(case 1, when there is no magnetic moment): there is no electric charge: Photon
A photon with a circular polarization has a spin and its T-symmetry is broken. However the photon does not have magnetic moment, because it has no charge
![]()
![]() (case 2, when there is no magnetic moment): T- symmetry is not broken: Quantum state filled by two electrons of opposite spins.
(case 2, when there is no magnetic moment): T- symmetry is not broken: Quantum state filled by two electrons of opposite spins.
The charge of such a quantum state is -2e. However, since the spin of this quantum state is zero, its T-symmetry is not broken. As a result, this quantum state does not have a magnetic moment.
--------------------
Photon has spin, but does not have a magnetic moment |
|---|
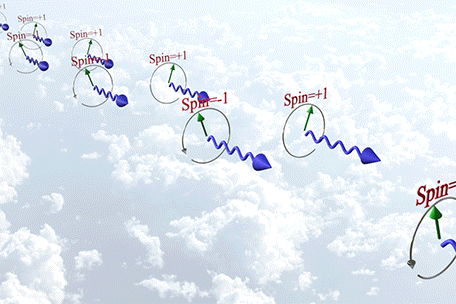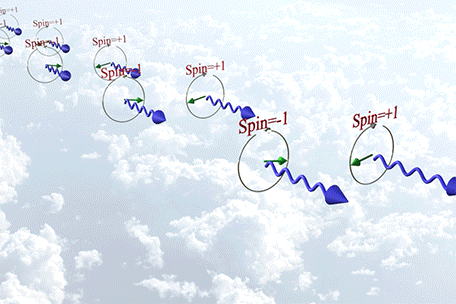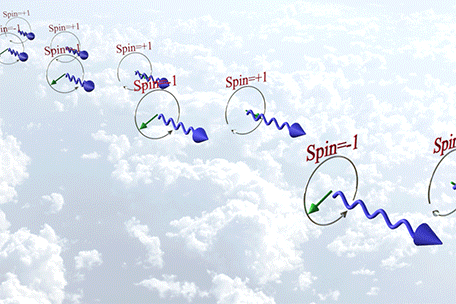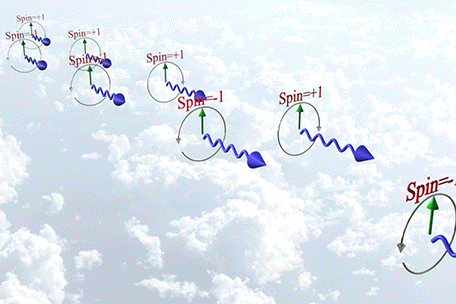 |
| Time-reversal symmetry (T-symmetry) is broken for a circularly polarized photon, but the photon does not have a magnetic moment because it lacks an electric charge. |
| click on image to enlarge it |
------------------

![]() (Measurement method 1): From ferromagnetic resonance or from electron paramagnetic resonance.
(Measurement method 1): From ferromagnetic resonance or from electron paramagnetic resonance.
The g-factor characterizes the precession frequency (Larmor frequency) of the magnetic moment in an external magnetic field. By measuring the precession frequency of the magnetic moment, the g-factor can be determined. This method involves observing the temporal change in the direction of the magnetic moment, from which the precession frequency and consequently the g-factor are evaluated
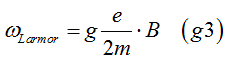
![]() (Measurement method 2): from Zeeman effect= from energy splitting.
(Measurement method 2): from Zeeman effect= from energy splitting.
The g-factor describes the energy difference for an electron, whose magnetic moment is directed along and opposite to the direction of the magnetic field. . By measuring the energy splitting as a function of the external magnetic field, the g-factor can be determined. Typically, this energy splitting is measured by observing the difference between two light absorption peaks corresponding to the magnetic moment's alignment parallel and antiparallel to the external magnetic field.
 Key difference between magnetic moments due to spin and due to orbital momentum
Key difference between magnetic moments due to spin and due to orbital momentum| Magnetic moment due to orbital momentum does not interact with magnetic field of spin- orbit interaction |
|---|
 |
| (reason) The magnetic field from spin-orbit interaction exists only in the reference frame that moves with the electron. In this coordinate system, the electron remains stationary at a single point and, as a result, does not possess an orbital momentum. |
| click on image to enlarge it |
![]() (fact): The key difference between magnetic moments due to spin and those due to orbital momentum lies in their interaction with the magnetic field Hso of spin-orbit interaction. The magnetic moment due to spin does interact with Hso, whereas the magnetic moment due to orbital momentum does not.
(fact): The key difference between magnetic moments due to spin and those due to orbital momentum lies in their interaction with the magnetic field Hso of spin-orbit interaction. The magnetic moment due to spin does interact with Hso, whereas the magnetic moment due to orbital momentum does not.
 (reason): relativistic origin of the magnetic field Hso of spin-orbit interaction
(reason): relativistic origin of the magnetic field Hso of spin-orbit interaction
The relativistic origin of the magnetic field Hso of spin-orbit interaction means that In the reference frame moving with the electron, a portion of the electric field is transformed into a magnetic field, known as Hso. In this coordinate system, the electron remains stationary at a single point, lacks orbital momentum, and thus does not have a magnetic moment due to orbital momentum.
Different Coordinate Systems and absence of Interactions between Hso and orbital:
![]() (In the coordinate system stationary with respect to the electric field):
(In the coordinate system stationary with respect to the electric field):
The electron moves and has orbital momentum.
There is no magnetic field Hso of spin-orbit interaction.
Consequently, there is no interaction between Hso and the magnetic moment due to orbital momentum.
![]() (In the coordinate system moving with the electron):
(In the coordinate system moving with the electron):
The electron remains stationary at a single point. Consequently, the electron does not possess orbital momentum.
There is magnetic field Hso of spin-orbit interaction.
Consequently, there is no interaction between Hso and the magnetic moment due to orbital momentum.
![]() (fact): The spin remains unchanged in both stationary and moving coordinate systems. Therefore, the magnetic moment due to spin interacts with the magnetic field Hso of spin-orbit interaction.
(fact): The spin remains unchanged in both stationary and moving coordinate systems. Therefore, the magnetic moment due to spin interacts with the magnetic field Hso of spin-orbit interaction.
![]() (fact): The interaction of the magnetic field Hsoof spin- orbit interaction exclusively with the magnetic moment due to spin, and not with the magnetic moment due to the orbital momentum, adds to the complexity of the g-factor's properties and behavior.
(fact): The interaction of the magnetic field Hsoof spin- orbit interaction exclusively with the magnetic moment due to spin, and not with the magnetic moment due to the orbital momentum, adds to the complexity of the g-factor's properties and behavior.
 (important note) : This enlargement occurs only for the spin, but not for the orbital moment.
(important note) : This enlargement occurs only for the spin, but not for the orbital moment. 
 (mechanism): Additional Contribution from the Magnetic Field of Spin-Orbit Interaction
(mechanism): Additional Contribution from the Magnetic Field of Spin-Orbit Interaction
![]() Calculation of enlargement of g-factor due to spin-orbit interaction:
Calculation of enlargement of g-factor due to spin-orbit interaction:
When an external magnetic field is applied, it generates an additional magnetic field Hsodue to spin-orbit interaction. Consequently, the electron experiences the combined effect of the external magnetic field and the spin-orbit interaction magnetic field Hso. For example, the electron's precession around the external magnetic field becomes faster than it would be without spin-orbit interaction. The Larmor frequency can be calculated as:

where kSO is coefficient of spin-orbit interaction, gs is the g-factor in absence of spin- orbit interaction.
From Eq. (g4), the Larmor frequency is calculated as
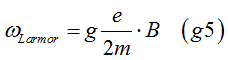
where the effective g-factor is
![]()
![]() (note): the effective g-factor is always larger than the g-factor gs in absence of spin- orbit interaction.
(note): the effective g-factor is always larger than the g-factor gs in absence of spin- orbit interaction.

![]() (note): about localized and conduction/ valence electrons
(note): about localized and conduction/ valence electrons
The value of the g-factor is primarily determined by conduction and valence electrons, rather than by localized electrons. This is because the size of conduction and valence electrons is large and approximately matches the size of photons, making their interaction with light highly effective. In contrast, localized electrons have a much smaller size resulting in weaker interactions with photons.
![]() (exception): ferromagnetic metals
(exception): ferromagnetic metals
All localized electrons in a ferromagnetic metal are interconnected through strong exchange interactions, forming a single collective object. The size of this collective object is large and comparable to the wavelength of a photon, leading to an efficient interaction between the localized electrons and electromagnetic radiation such as light or microwaves. A notable example of this effective interaction is Ferromagnetic Resonance (FMR).
The g- factor of ferromagnetic metals is slightly larger than 2. (e.g. Fe g=2.088; Co g=2.18;Ni g=2.2)
(reason): In a ferromagnetic metal, localized electrons are the primary contributors to the g-factor. These electrons have quenched orbital moments, meaning their orbital contribution is nearly zero, and only their spin contributes to the g-factor. The g-factor due to the spin is 2.
Additionally, localized electrons experience spin-orbit interaction. This means that, in addition to the externally applied magnetic field, there is an internal magnetic field from the spin-orbit interaction. This internal field enhances the magneto-optical interaction, causing the g-factor to be larger than 2.
The g-factor of a semiconductor can vary widely, ranging from large negative values to moderate positive values.(e.g. GaAs g=-0.3; Si g=+2.0;InSb g=-51.3)
(fact:) main contribution from conduction & valence electrons
In a semiconductor, conduction and valence electrons are the primary contributors to the g-factor. The orbital moment of these electrons is unquenched and both the spin and the orbital moment contribute to the g-factor. The contribution of the orbital moment is more substantial for valence electrons. For example, in silicon, the g-factor for conduction electrons is approximately 2.0 (spin-dominated), while for valence electrons, it is around 1.1 (indicating a significant orbital moment contribution).
(fact) Large value of g- factor
In a semiconductor, the g-factor can be significantly different from 2 and 1. This indicates that the actual magnetic field experienced by an electron under an external magnetic field is substantially larger than the external field itself. The external magnetic field Hext generates an additional magnetic field Hso due to spin-orbit interaction. In semiconductors, Hso is often large and can exceed Hext. As a result, an electron experiences the combined effect of Hso and Hext, which is often substantially larger than the external field alone.
(fact) Frequent negative value of g- factor
Many semiconductors have a negative g-factor. A negative g-factor means that the actual magnetic field experienced by an electron under an external magnetic field is opposite to the direction of the external field. The external magnetic field Hext generates an additional magnetic field Hso due to spin-orbit interaction.
The magnetic field Hso arises from two opposing contributions: the clockwise-rotating component and the counterclockwise-rotating component of the electron orbital. In the absence of Hext, these two components are equal and cancel each other out, resulting in no Hso. However, the external field creates a Lorentz force, which acts in opposite directions on these two components, altering their distributions differently. This imbalance results in a non-zero Hso.
Depending on how each component is modified, Hso can either align with or oppose Hext. Since Hso is often larger than Hext, the overall magnetic field (Hso+Hext) can have a polarity opposite to that of Hext.
(fact) Different value of g-factor for conduction and valence electrons.
In a
(fact) A narrow- band semiconductors have a largest absolute value of the g-factor.
In a

| Timing of spin alignment along orbital moment |
|---|
| Balance between electron scattering time and spin alignment time |
 |
| click on image to enlarge it. smaller size is here |
![]()
![]() (fact 1): There is no direct interaction between spin and orbital moment
(fact 1): There is no direct interaction between spin and orbital moment
![]()
![]() (fact 2): Often (but not always) the magnetic field HSO of spin- orbit interaction is aligned along the orbital moment. The spin is aligned along HSO in order to minimize its magnetic energy.As a result, the spin aligns along the orbital moment as well.
(fact 2): Often (but not always) the magnetic field HSO of spin- orbit interaction is aligned along the orbital moment. The spin is aligned along HSO in order to minimize its magnetic energy.As a result, the spin aligns along the orbital moment as well.
![]()
![]() (fact 3): When an electron is scattered into an empty quantum state, its spin is initially randomly aligned with respect to Hso and the orbital moment. Subsequently, spin precession occurs around HSO. Additionally, there is precession damping leading the spin to align along HSO to minimize magnetic energy. The process of spin alignment is moderate in speed, requiring a noticeable amount of time for the spin to fully align with the orbital moment.
(fact 3): When an electron is scattered into an empty quantum state, its spin is initially randomly aligned with respect to Hso and the orbital moment. Subsequently, spin precession occurs around HSO. Additionally, there is precession damping leading the spin to align along HSO to minimize magnetic energy. The process of spin alignment is moderate in speed, requiring a noticeable amount of time for the spin to fully align with the orbital moment.
: :
:
Whether the spin aligns with the orbital moment in a specific material is determined by the balance between electron scattering time and spin alignment time along HSO. If the scattering time is significantly shorter than the alignment time, the spins and orbital moments remain unaligned. Conversely, if the scattering time is substantially longer than the alignment time, the spins and orbital moments become fully aligned.

![]() How and why does a magnetic field break time- inverse symmetry (T- symmetry)??
How and why does a magnetic field break time- inverse symmetry (T- symmetry)??
 (absence of magnetic field): In the case of a quenched electron, whose orbital moment is zero, the orbital motion can be divided into clockwise and counterclockwise paths around a nucleus. During rotation along each path, the electron experiences an equal but opposite magnetic field of spin-orbit interaction. Consequently, the net effect is that the electron experiences no spin-orbit interaction.
(absence of magnetic field): In the case of a quenched electron, whose orbital moment is zero, the orbital motion can be divided into clockwise and counterclockwise paths around a nucleus. During rotation along each path, the electron experiences an equal but opposite magnetic field of spin-orbit interaction. Consequently, the net effect is that the electron experiences no spin-orbit interaction.
 (breaking T-symmetry by a magnetic field): A magnetic field breaks T- symmetry for an electron orbita due to the following mechanism: The magnetic field creates the Lorentz force. This force affects the electron differently along its clockwise and counterclockwise paths. It pushes the clockwise-rotating part of the electron wavefunction away from the nucleus while drawing the counterclockwise-rotating part closer to it. This disparity in the electric field of the nucleus experienced by the electron for these two opposite rotations disrupts the equilibrium between opposing magnetic fields of spin-orbit interaction, resulting in a significant magnetic field of spin-orbit interaction experienced by the electron.
(breaking T-symmetry by a magnetic field): A magnetic field breaks T- symmetry for an electron orbita due to the following mechanism: The magnetic field creates the Lorentz force. This force affects the electron differently along its clockwise and counterclockwise paths. It pushes the clockwise-rotating part of the electron wavefunction away from the nucleus while drawing the counterclockwise-rotating part closer to it. This disparity in the electric field of the nucleus experienced by the electron for these two opposite rotations disrupts the equilibrium between opposing magnetic fields of spin-orbit interaction, resulting in a significant magnetic field of spin-orbit interaction experienced by the electron.
![]() What is special about the magnetic field that it breaks T-symmetry?
What is special about the magnetic field that it breaks T-symmetry?
A magnetic field breaks time-inverse symmetry (T-symmetry) due to the fundamental nature of magnetic interactions in physics. The concept stems from the behavior of magnetic fields under time reversal, which refers to the reversal of the direction of time. In classical physics, T-symmetry implies that the laws of physics remain the same whether time progresses forward or backward.
However, when considering magnetic fields, particularly in the context of spin-orbit interactions, T-symmetry is broken. This occurs because the behavior of magnetic fields changes direction under time reversal. For instance, if you reverse the direction of time, the magnetic field produced by a current-carrying wire would also reverse its direction. This property of magnetic fields under time reversal is a fundamental aspect of their nature.
| Lorentz Force: The Mechanism Behind Magnetic Field-Induced Spin-Orbit Interaction |
|---|
 |
| Lorentz force describes the fact that an object (shown as a red ball), which is moving in a static magnetic field, experiences an effective electrical field. |
(in absence of magnetic field): ![]()
![]()
Full quenching indicates that the orbital moment is zero, allowing the electron wavefunction to be divided into two components corresponding to clockwise and counterclockwise motions. In the absence of both external magnetic fields and the orbital moment, these two components encounter magnetic fields from spin-orbit interaction that are equal in magnitude but opposite in direction. Consequently, these contributions balance each other, leading to a cancellation of net spin-orbit interaction for the electron.This is the case when T-symmetry is unbroken for the orbital. Reversing the flow direction of time causes an interchange between clockwise and counterclockwise components of the electron wavefunction, which, in this case, doesn't alter anything.
a
(in presence of magnetic field): ![]()

In order for spin-orbit interaction to exist, there must be a discernible difference between orbital clockwise and counterclockwise rotations, which signifies the disruption of T-symmetry. This symmetry can be externally broken by applying a magnetic field, which creates the Lorentz force. The direction of the Lorentz force is opposite for the clockwise- and counterclockwise- rotating components of the electron wavefunction. The force pushes the clockwise-rotating part of the electron wavefunction away from the nucleus while drawing the counterclockwise-rotating part closer to it. This creates a disparity in the electric field of nucleus experienced by the electron for these two opposite rotations. Consequently, the balance between opposing magnetic fields of spin-orbit interaction is disrupted, leading to a significant overall magnetic field of spin- orbit interaction experienced by the electron.
Lorentz Force: The Mechanism Behind Magnetic Field-Induced Spin-Orbit Interaction |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||
| click on image to enlarge it |
![]() (spin- orbit interaction & Zeeman splitting): Is the existence of this type of spin-orbit interaction related to Zeeman splitting and proportional to Zeeman energy?
(spin- orbit interaction & Zeeman splitting): Is the existence of this type of spin-orbit interaction related to Zeeman splitting and proportional to Zeeman energy?
No, the Zeeman splitting refers to the variation in energy levels experienced by an electron in a magnetic field, depending on its spin orientation. The Zeeman energy represents the energy difference between the electron's spin alignment opposite and along the magnetic field.
In contrast, the Lorentz force alters the spatial distribution of the electron's wavefunction, creating a distinction between its clockwise and counterclockwise rotational components. This discrepancy leads to an imbalance in the opposing contributions of these components to the spin-orbit interaction, thereby giving rise to an overall spin-orbit interaction. Importantly, this mechanism is not related to the electron's spin itself.


While even a perfectly symmetrical spherical orbital experiences some level of spin-orbit interaction (SO), it remains relatively weak. However, SO interaction significantly amplifies in deformed orbitals, such as elliptical ones. Additionally, when the center of an electron's orbital shifts from the nucleus position, the strength of the spin-orbit interaction substantially increases.
Enhanced Spin-Orbit Interaction in Asymmetric Orbitals |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
| (note: simplified schematic): the figures shown above are simplified schematic representation of the electron orbital aiming to demonstrate the operation principle of the effect. | |||||||||
| click on image to enlarge it |
![]() Dual Impacts of Orbital Deformation:
Dual Impacts of Orbital Deformation:
 (impact 1): spin-orbit interaction becomes anisotropic
(impact 1): spin-orbit interaction becomes anisotropic
For the same external magnetic field applied in different directions, the strength of the magnetic field of spin- orbit interaction becomes very different.
 (impact 2): spin-orbit interaction becomes stronger
(impact 2): spin-orbit interaction becomes stronger
Under identical external magnetic field strength, the magnetic field of spin-orbit interaction significantly intensifies.
| Dual Impacts of Orbital Deformation on Spin-Orbit Interaction | ||||||
|---|---|---|---|---|---|---|
|
||||||
| click on image to enlarge it |
![]() Under what circumstances is the electron orbital deformed?
Under what circumstances is the electron orbital deformed?
(case 1) at interface
At an interface, the atomic environment differs from that of the bulk, leading to orbital reconstruction or deformation. The attraction force exerted by neighboring orbitals above and below the interface varies significantly, causing elongation of the orbital at the interface and a shift in its position relative to its nucleus. This process results in anisotropic spin-orbit interaction with a substantially increased SO strength.
(case 2) anisotropic material
An anisotropic material comprises diverse atoms. The electron orbital, enveloped by atoms of varying types, encounters different forces from different directions. This leads to the elongation of the orbital and a shift in its position relative to the nucleus. Consequently, anisotropic spin-orbit interaction emerges with significantly increased strength.
In a crystal, the deformation of the orbital and its impact on spin-orbit interaction are contingent upon neighboring atoms. Proximity to a neighbor can either push the electron orbital away or draw it closer to the atomic nucleus, a process that varies in different directions.
(case 3) under a gate voltage (VCMA effect)
When an external electrical field is applied, it exerts a force on the electron in a particular direction, leading to the elongation of the orbital and a displacement of its position relative to the nucleus. This results in a change in the strength of the spin-orbit interaction.
 Magnetic anisotropy & Spin- orbit interaction
Magnetic anisotropy & Spin- orbit interaction 
Magnetic anisotropy describes the variation in magnetic properties of a ferromagnetic material based on the direction of its magnetization. The ferromagnetic material possesses an easy magnetic axis, along which magnetization results in the lowest magnetic energy, making it the equilibrium magnetization direction. An external magnetic field is required in order to tilt the magnetization out of the easy axis. The magnetic anisotropy is the reason why the magnetic field of a permanent magnet is directed in only one direction.
![]() (fact): The spin- orbit interaction is the major factor originating the magnetic anisotropy. Another contributor is the demagnetization field.
(fact): The spin- orbit interaction is the major factor originating the magnetic anisotropy. Another contributor is the demagnetization field.
 (origin of magnetic anisotropy): Magnetic anisotropy arises from the significant variation in the strength of spin-orbit interaction concerning the orientation of the applied external magnetic field relative to the symmetry axis (deformation axis) of an electron orbital.
(origin of magnetic anisotropy): Magnetic anisotropy arises from the significant variation in the strength of spin-orbit interaction concerning the orientation of the applied external magnetic field relative to the symmetry axis (deformation axis) of an electron orbital.
![]() How and why does an electron current break time- inverse symmetry (T- symmetry)??
How and why does an electron current break time- inverse symmetry (T- symmetry)??
 (absence of electron current): Even in the absence of an electron current, there are spin-dependent scatterings due to spin- orbit interaction. However, such spin-dependent scatterings are very uniform. Although the probability of each scattering depends on the electron's spin direction, there are equal amounts of scattering in any two opposite directions. As a result, there are no overall preferential spin effects.
(absence of electron current): Even in the absence of an electron current, there are spin-dependent scatterings due to spin- orbit interaction. However, such spin-dependent scatterings are very uniform. Although the probability of each scattering depends on the electron's spin direction, there are equal amounts of scattering in any two opposite directions. As a result, there are no overall preferential spin effects.
 (breaking T-symmetry by an electron current): When there is an electron current, more electrons flow in the current direction than in the opposite direction. In this case, the difference in the numbers of electrons scattered into two opposite directions depends on the electron's spin. This results in spin accumulation in one direction compared to the opposite direction. This scattering-induced spin accumulation occurs either at the left/right sides with respect to the current direction or toward/opposite to the current direction.
(breaking T-symmetry by an electron current): When there is an electron current, more electrons flow in the current direction than in the opposite direction. In this case, the difference in the numbers of electrons scattered into two opposite directions depends on the electron's spin. This results in spin accumulation in one direction compared to the opposite direction. This scattering-induced spin accumulation occurs either at the left/right sides with respect to the current direction or toward/opposite to the current direction.
![]() Spin-dependent scattering refers to the phenomenon where the probability of scattering for a conduction electron varies based on its spin direction.
Spin-dependent scattering refers to the phenomenon where the probability of scattering for a conduction electron varies based on its spin direction.
Example: The scattering probability for a spin-up electron is higher towards the left direction, while the scattering probability for a spin-down electron is higher towards the right direction, relative to the direction of the electron current. In this case:
![]() (example 1) Spin Hall effect (accumulation of spin- polarized electrons at opposite sides of a metallic wire)
(example 1) Spin Hall effect (accumulation of spin- polarized electrons at opposite sides of a metallic wire)
In a non-magnetic metal at equilibrium, the numbers of electrons with opposite spin directions are equal. When an electron current flows, spin-dependent scatterings tend to move more spin-up electrons to the left and more spin-down electrons to the right. Consequently, spin-up electrons accumulate on the left side of the wire, while spin-down electrons accumulate on the right side.
![]() (example 2) Inverse Spin Hall effect (ISHE) (accumulation of a charge at opposite sides of a metallic wire, which is proportional to spin- polarization of the conduction electrons)
(example 2) Inverse Spin Hall effect (ISHE) (accumulation of a charge at opposite sides of a metallic wire, which is proportional to spin- polarization of the conduction electrons)
When the magnetization of the ferromagnetic metal is oriented upwards, the spins of spin-polarized conduction electrons align similarly upwards and, therefore, more electrons are scattered towards the left direction compared to the right. Consequently, electrons accumulate on the left side of the wire, resulting in a negative charge on that side. Conversely, electrons are depleted on the right side, leading to a positive charge on that side. It results in the Hall voltage between the left and right sides of the wire.
 Spin- orbit interaction as origin of Spin- dependent scatterings -->
Spin- orbit interaction as origin of Spin- dependent scatterings -->
spin- orbit interaction as origin of spin- dependent scatterings and, as a consequence, as an origin of spin- transport effects |
||||||
|
||||||
The electron is scattering from a quantum state, which does not experience any spin- orbit interaction to a state where the magnetic field of spin- orbit interaction is directed up. |
||||||
The spin-dependency of electron scattering is the origin for a variety of magneto-transport effects. |
||||||
(fact) Local nature of spin- orbit interaction is he basis for a variety of magneto-transport effects. |
||||||
| Spin-dependency of electron scatterings is substantial for scatterings across the interface and scatterings in the vicinity of an interface. For instance, when an electron scatters across an interface, it encounters a markedly different spin-orbit interaction field on either side of the interface. | ||||||
| click on image to enlarge it |
 Local Nature of spin- orbit interaction as a Key Factor making electron scatterings spin- dependent:
Local Nature of spin- orbit interaction as a Key Factor making electron scatterings spin- dependent:
The strength of spin-orbit interaction can vary significantly for individual orbitals. Two neighboring electrons in closely situated orbitals may experience markedly different strengths of spin-orbit interaction. Consequently, after a scattering event, an electron may encounter a greatly varying strength of spin-orbit interaction. As the magnetic energy differs for electron spin aligned with and opposite to the spin-orbit interaction's magnetic field, the final energy of the scattered electron—and hence the electron scattering probability—is influenced by the electron's spin orientation.
This unique locality of the magnetic field Hso of spin- orbit interaction plays a key role in the origins of numerous magneto-transport phenomena, such as the Spin Hall effect and Anomalous Hall effect, etc. This locality of Hso plays a decisive role in making electron scattering spin-dependent. When an electron is scattered to a nearby or the same point but a different quantum state, it encounters a distinct Hso. Consequently, the magnetic energy of the electron's final state varies with the direction of its spin, leading to a difference of scattering probabilities based on the spin direction of the scattered electron. This spin-preferential scattering results in spin accumulation. Consequently, electron currents generate spin accumulation and the properties of the electron current become spin- dependent. The diverse manifestations of this effect give rise to a spectrum of magneto-transport phenomena.
The magnetic field Hso of spin-orbit interaction is created by the electric field of the nucleus resulting from the electron's orbital rotation around it. Consequently, Hso is heavily influenced by the orbital's shape and symmetry relative to the nucleus's position. Given that neighboring orbitals can possess vastly different shapes and symmetries, they experience correspondingly distinct Hso values.
The family of magneto-transport effects refers to phenomena where the properties of an electron current are influenced by external factors, which break the T- symmetry, like the magnetic field, material magnetization (total spin of localized electrons), the spin polarization (total spin of conduction electrons). This can result in changes in resistance (magneto- resistance) or in accumulations of charge and/or spin at the sides of the wire (the Hall effect).

![]() (Important note 1 about electron current): scatterings & current
(Important note 1 about electron current): scatterings & current
Electron scatterings play a pivotal role in defining the properties of electron current. There are only a few cases when it is not the case. For instance, superconducting currents or tunneling currents are examples where electron scatterings are absent, leading to a vastly different behavior compared to conventional current flow.
![]() (Important note 2 about electron current): conduction & localized electrons
(Important note 2 about electron current): conduction & localized electrons
In a solid, electrons can be categorized into two types: localized and conduction electrons.
Localized electrons have a small size, roughly that of an atom. As a result, these electrons have minimal overlap with other electrons, making their scattering occurrences very rare. Consequently, localized electrons do not actively participate in the electron current.
Conversely, conduction electrons have a larger size and overlap with billions of other conduction electrons. This results in frequent scattering of conduction electrons. Therefore, it is the conduction electrons that predominantly contribute to the electron current.
Spin Hall effect |
|---|
 |
(definition)  The Spin Hall effect refers to the accumulation of spin at the sides of a metallic wire when an electron current flows through it. The Spin Hall effect refers to the accumulation of spin at the sides of a metallic wire when an electron current flows through it. |
| (mechanism): Conduction electrons (shown by green balls) undergo scattering on a charged defect (blue ball). These conduction electrons are spin-unpolarized, meaning their spins are equally distributed in all directions. However, due to the spin-orbit interaction, spin-up electrons have a higher probability of scattering to the right than to the left, while spin-down electrons have a lower probability of scattering to the right than to the left. Consequently, spin-up electrons accumulate at the right side of the wire, while spin-down electrons accumulate at the left side. |
| (note) The Spin Hall effect redistributes spin-unpolarized electrons (with spins oriented in all directions) into two distinct locations, where either the number of spin-up or spin-down electrons is higher. Overall, the total number of electrons with a specific spin direction remains unchanged. It does not realign electron spins, as a magnetic field would, for example. (See here and here) |
| click on image to enlarge it |
![]() (Important note 3 about electron current): groups of spin- polarized & spin- unpolarized electrons
(Important note 3 about electron current): groups of spin- polarized & spin- unpolarized electrons
In a ferromagnetic metal, the conduction electrons are spin- polarized, dividing them into two distinct groups. In the groups of spin- unpolarized electrons, the electron spins are distributed equally in all directions. In the groups of spin- polarized electrons, all electrons have their spins aligned in one direction.
Different magneto-transport effects impact either spin-polarized or spin-unpolarized electrons, depending on the specific effect under consideration.
![]() (Important note 4 about electron current): movement of electrons even in absence of current
(Important note 4 about electron current): movement of electrons even in absence of current
Even in the absence of an electron current, all conduction electrons move at relatively high speeds. However, an equal number of electrons move in any two opposite directions, leading to an equilibrium where no net charge or spin transfer occurs on average.
When an electric field is applied, more electrons move along the field direction than in the opposite direction. This discrepancy results in the transport of both charge and spin.
It's important to note that electron current does not imply that electrons are stationary in the absence of an electric field and only start moving under its influence. Rather, electrons are continually in motion at nearly similar speeds regardless of the presence of an electric field. However, the electric field alters the probability of electron scattering, leading to different numbers of electrons moving along and against the field direction.
The Spin Hall effect describes the fact that a spin current is generated perpendicularly to an electrical charge current in a metallic wire.
The Spin Hall effect doesn't necessitate an external field to break T-symmetry and can occur in both non-magnetic and ferromagnetic metals.
 (mechanism):
(mechanism):
In a non-magnetic metal at equilibrium, the numbers of electrons with opposite spin directions are equal. When an electron current flows, spin-dependent scatterings tend to move more spin-up electrons to the left and more spin-down electrons to the right. Consequently, spin-up electrons accumulate on the left side of the wire, while spin-down electrons accumulate on the right side.
 (electrons affected): Spin- unpolarized conduction electrons
(electrons affected): Spin- unpolarized conduction electrons
These effects are linearly proportional to either an external magnetic field Hext , the total spin Slocal of localized d- electrons or the total spin Scond of conduction electrons
Famaly of Hall effects: ISHE, AHE and OHE |
|---|
 |
| Hall effect describes the fact that charge is accumulated at sides of metallic wire, when the magnetization (Anomalous Hall effect) or the external magnetic field H (Ordinary Hall effect ) or spins of spin- polarized conduction electrons (Inverse Spin Hall effect ) is directed perpendicularly to the wire. |
| click on image to enlarge it |
All three effects describe the charge accumulation at the sides of a metallic wire due to either an external magnetic field (OHE), magnetization (AHE), or spin polarization of conduction electrons (ISHE).
It is because all three effects are linearly proportional to the external field, which breaks the T-symmetry. Such a field can be either an external magnetic field (OHE), the total spin of localized electrons (AHE), or the total spin of conduction electrons (ISHE).
 (mechanism): Inverse Spin Hall effect (ISHE)
(mechanism): Inverse Spin Hall effect (ISHE)
When the magnetization of the ferromagnetic metal is oriented upwards, the spins of spin-polarized conduction electrons align similarly upwards and, therefore, more electrons are scattered towards the left direction compared to the right. Consequently, electrons accumulate on the left side of the wire, resulting in a negative charge on that side. Conversely, electrons are depleted on the right side, leading to a positive charge on that side. It results in the Hall voltage between the left and right sides of the wire.
 (mechanism): Anomalous Hall effect (AHE)
(mechanism): Anomalous Hall effect (AHE)
The origin of the Anomalous Hall effect (AHE) lies in a difference of scattering probabilities for conduction electrons, depending on the direction of electron movement relative to the spin direction of localized electrons. For instance, when electrons move forward and the spins of localized electrons point upward, the probability of scattering to the right is higher than to the left. Conversely, if the electron moves in the opposite direction or the spin direction is reversed, the scattering probabilities reverse: the probability of scattering to the right is larger compared to scattering to the left.
Even in the absence of an electrical current, this difference in scattering probabilities exists. However, the preferential scattering to the left for forward-moving electrons is exactly compensated by the preferential scattering to the right for backward-moving electrons, resulting in no net Hall current.
When an electrical current is present in the forward direction, more electrons move forward, disrupting the balance between left and right scatterings. This imbalance causes more electrons to scatter to the left, generating a Hall current in that direction.
origin of Ordinary Hall effect : Lorentz force |
|---|
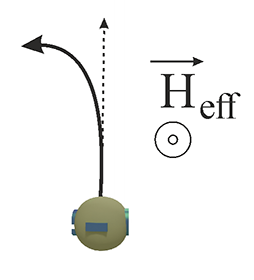 |
| The Lorentz force deflects the electron (green ball) from its straight path. An electron moving in a magnetic field H experiences an electric field perpendicular to its motion due to relativistic effects. This electric field interacts with the electron's charge, altering its direction of movement. As a result, an electron current (Hall current) is generated perpendicular to the bias current. |
| click on image to enlarge it |
 (mechanism): Ordinary Hall effect (OHE)
(mechanism): Ordinary Hall effect (OHE)
The origin of the Ordinary Hall Effect (OHE) is the Lorentz force. An electron moving perpendicularly to a magnetic field experiences a relativistic electric field. This electric field interacts with the electron's charge (not its spin), creating the Lorentz force. This force causes the electron to deflect in a direction perpendicular to both the magnetic field and its initial movement.
---------------------------------------------------------
 (electrons affected):
(electrons affected):
(Inverse Spin Hall effect (ISHE)): Spin- polarized conduction electrons
(Anomalous Hall effect (AHE)): All conduction electrons
(Ordinary Hall effect (OHE)): All conduction electrons
--------------------
![]() (direction): Hall current flows perpendicular to the wire and perpendicular to the conventional electrical current flowing along to wire due to applied voltage V.
(direction): Hall current flows perpendicular to the wire and perpendicular to the conventional electrical current flowing along to wire due to applied voltage V.
--------------------
 (Math formula):
(Math formula):
(Inverse Spin Hall effect (ISHE)): ![]() or the same
or the same ![]()
(Anomalous Hall effect (AHE)): ![]() or the same:
or the same: ![]()
(Ordinary Hall effect (OHE)): ![]()
where jHall is electrical current flowing perpendicular to wire; jV is conventional electrical current flowing along to wire due to applied voltage V; Ps is spin polarization. m is unity vector along spin- direction of spin-polarized conduction electrons; Sconduct is the total spin of conduction electrons; M is the magnetization; Slocal is the total spin of localized electrons; H is external magnetic field; aIIHE is the rotation angle of the Inverse Spin Hall effect (in mdeg); aAH is the rotation angle of the Anomalous Hall effect (in mdeg); aOH is the rotation angle of the ordinary Hall effect (in mdeg/kG).
| Anisotropic Magneto Resistance (AMR) & Planar Hall effect (PHE) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||
| Sample Volt 54a R13C (see here about sample details) | ||||||||||||
| click on image to enlarge it |
It is because these effects are proportional to the product of two independent parameters from a set: 1.an external magnetic field, 2. the total spin of localized d- electrons (magnetization) and 3. the total spin of conduction electrons (spin polarization), each of which breaks time-reversal (T) symmetry.
 (electrons affected): spin- polarized conduction electrons.
(electrons affected): spin- polarized conduction electrons.
 (mechanism):
(mechanism):
mechanism of Anisotropic magnetoresistance/ Planar Hall effect (AMR/PHE):
Kondo- type contribution (main contribution):
The effect originates from the dependence of the conduction electron scattering probability on the spin direction of the conduction electron relative to both the spin direction of the localized electrons and the direction of the electron movement. As a result, the electron scattering probability differs depending on whether the scattered direction is along or opposite to the spin direction of the localized electrons, leading to a magnetic current flowing in that direction.
 (Math formula):
(Math formula): ![]()
----------
![]() (direction): Magnetic current flows along magnetization direction.
(direction): Magnetic current flows along magnetization direction.
![]() Why two names?
Why two names?
 Anisotropic magnetoresistance (AMR), which describes the magnetic change in resistance, and the Planar Hall Effect (PHE), which describes the Hall voltage, are two different manifestations of a single underlying effect. It took me considerable time and effort to convince the research community of this fact.
Anisotropic magnetoresistance (AMR), which describes the magnetic change in resistance, and the Planar Hall Effect (PHE), which describes the Hall voltage, are two different manifestations of a single underlying effect. It took me considerable time and effort to convince the research community of this fact.

![]()
![]() Except of a few weak effects, all spin-orbital effects are induced by an electrical field of an atomic nucleus and the election movement (rotation) in the close proximity of the nucleus !!
Except of a few weak effects, all spin-orbital effects are induced by an electrical field of an atomic nucleus and the election movement (rotation) in the close proximity of the nucleus !!
![]() Magnitude of the spin-interaction in is small when an conduction electron moves in any realistic extrinsic or intrinsic electrical field in a solid!!!.
Magnitude of the spin-interaction in is small when an conduction electron moves in any realistic extrinsic or intrinsic electrical field in a solid!!!.
a moderate electrical field + a moderate electron speed => result: a very small spin-orbit interaction
![]() Except for an electron, which moves in a close vicinity of an atomic nucleus
Except for an electron, which moves in a close vicinity of an atomic nucleus
a very strong electrical field + a moderate electron speed => result: a strong spin-orbit interaction
Example 1.
When the orbital of an electron is center-symmetrical, the orbital moment and spin-orbit interaction can be zero despite of electron rotation around nucleus |
||||||
s- orbit of an atom |
||||||
|---|---|---|---|---|---|---|
|
||||||
Both representation of the electron orbital are equivalent. |
||||||
| Fig.8. s- orbital. An electron rotates around a nucleus in spherical orbital. Since at the same time the electron rotates in clockwise and anti clockwise directions, the spin-orbit interaction for opposite rotations cancels each other and the electron does not experience the spin-orbit interaction. | ||||||
| click on image to enlarge it |
Even in the of the highest-possible electron speed in solid and largest-possible applied electrical field, the effective magnetic field of the spin-orbit interaction is small!!
Electron Speed: Saturation Velocity :1E7 m/s (GaAs Si )
It is maximum drift speed of electrons in a solid.
The applied voltage: Breakdown voltage: 5E5 V/cm(GaAs, Si)
It is maximum voltage, which could be applied to a semiconductor (a oxide). For higher voltage the avalanche breakdown occurs.
![]() Result:
Result:
The effective magnetic field of the spin-orbit interaction is only 0.5 Gauss
![]() It is too small!!! For example, Earth's magnetic field at at the Earth's surface ranges from 0.25-0.65 Gauss.
It is too small!!! For example, Earth's magnetic field at at the Earth's surface ranges from 0.25-0.65 Gauss.![]()
Example 2.
Electron Speed: linear speed of electron rotating around atom : ~2.1E6 m/s
The applied voltage:Coulomb Electrical Field in H atom at 1st orbital (r=0.053 nm) 5.1E9 V/cm
Result:
It is rather large!!!. Such large magnetic field can only be obtained by a superconducting magnet.
Q. Both localized (-d,-f) and delocalized (-s,-p) electrons are rotating around nuclei (atoms), is it sufficient for them to experience a strong spin-orbit interaction?
A. No. It is far not sufficient. There are several other conditions the electron should satisfy in order to experience the spin-orbit interaction:
1) The orbital moment (symmetry) should be non-zero. Only electrons, which wave function has the -p,-d,-f- like spacial symmetry may experience the spin-orbit interaction.
2) The time-inverse symmetry should be broken!!
The following describes the reasons why an electron does not experience the spin-orbit interaction when the electron orbit is spherical and why it does experience the spin-orbit interaction for other shapes of the orbital.
Dirac equations calculates both contributions to the spin-orbit interaction (contribution 1) due to relativistic nature of the electromagnetic field. (contribution 2) due to relativistic nature of the quantum field of an electron.
Schrödinger equation calculates only contribution 1 due to relativistic nature of the electromagnetic field. It does not calculate contribution 2 due to relativistic nature of the quantum field of an electron.
The Einstein's relativistic equation for the energy is
![]()
which should describe the electron field as well. The quantum-mechanical for the energy and the momentum are
Substituting Eq.(3.2) into Eq.(3.2) gives Klein-Gordon equation as
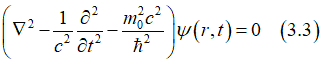
Considering limitation on the possible symmetries of the wave function, the wave equation should be 1st order differential equation with respect of time and space. Dirac has found that the Klein-Gordon equation can be represented as a product of 1st order differential equation and its conjugate. Therefore, such the wave equation fully describes the electron field.
![]()
where the gamma matrices (2 × 2 sub-matrices taken from the Pauli matrices)
The Dirac equation, which includes the gauge potential, is
![]()
Probably not. The Dirac equation and the Pauli equation, both do include the conservation of the time-inverse symmetry and spin. It is difficult to answer about the Klein-Gordon equation.
In this case wave function can be represented as a sum of a large "electron" part and a small "positron" part.
Yes, the effective magnetic field HSO should be used in Eq.(3.2) additionally to the external magnetic field. Then, the Pauli equation correctly describes the SO interaction
The gauge invariant A is the invariant for the Lorentz transformation, but the wave function of the Pauli equation is not a invariant. Therefore, in contrast to the Dirac equation the Pauli equation is not an invariant for the Lorentz transformation. The reason why HSO is not included into the Pauli equation, but should be input as additional magnetic field, is following. The Pauli equation is the equation, which is valid in only one static coordinate system. When an electron moves in this static coordinate system, the Pauli equation becomes not valid. The relativistic transformation of the quantum field of an electron are missing in Pauli equation. However, the adding of HSO fixes the problem and the Pauli equation becomes valid again.
![]() The Pauli equation is the extension of Schrödinger equation, where electron spin properties are included
The Pauli equation is the extension of Schrödinger equation, where electron spin properties are included
![]() The Pauli equation can be considered as a semi- relativistic equation. They place is between simpler, but approximate Schrödinger equation and full, but more complex Dirac equation.
The Pauli equation can be considered as a semi- relativistic equation. They place is between simpler, but approximate Schrödinger equation and full, but more complex Dirac equation.
![]() The Pauli equation can be obtained from the Dirac equation.
The Pauli equation can be obtained from the Dirac equation.
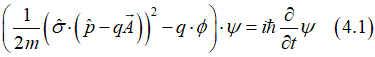
where A is the magnetic vector potential and is φ the electric scalar potential. σ is the Pauli matrices
The magnetic field can be calculated as
![]()
Substituting Eq.(4.2) into Eq.(4.2) gives
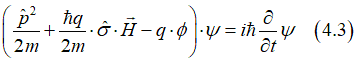
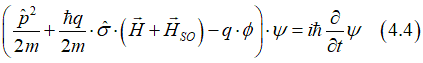
Energy of spin- orbit interaction |
 |
Fig.6 There is a precession of electron spin S around magnetic field HSO of spin-orbit interaction until it aligns parallel to HSO. After the electron spin is aligned, the energy of SO interaction becomes |
| click on image to enlarge it |
The spin-orbit interaction manifests itself only by the SO magnetic field HSO. The HSO is a very normal magnetic field (almost). There is a precession of electron spin S around magnetic field HSO of spin-orbit interaction until it aligns parallel to HSO. After the electron spin is aligned, the energy of SO interaction becomes
![]()
μB is the Bohr magneton
It is because of relativistic origin of both the SO interaction and the Lorentz force.
The HSO interacts only with the spin magnetic moment, but not with the orbital magnetic moment or the total magnetic moment
The HSO is the magnetic field of the relativistic origin. It appears only the coordinate system, which moves together with the electron (See here). The Lorentz force is of the relativistic origin as well and it is originated from the electrical field, which the electron experiences when moves in a magnetic field. In the moving coordinate system, where the electron experiences HSO , the electron does not move and therefore has no experience any Lorentz force
The interaction of the orbital moment with a magnetic field is due to the Lorentz force
Note: The total magnetic moment is a quantum- mechanical sum of the orbital magnetic moment and the spin-magnetic moment. The role holds for both cases when spin is align along HSO (along the orbital moment) and when the there is a spin precession around HSO.
![]() Electron spin is aligned along due the spin precession damping (See Fig.6). The spin precession damping is a complex mechanism (See here), which involves an external particle with a non-zero spin (e.g. a photon, a magnon). It could take a relatively a long until full alignment of electron spin along HSO.
Electron spin is aligned along due the spin precession damping (See Fig.6). The spin precession damping is a complex mechanism (See here), which involves an external particle with a non-zero spin (e.g. a photon, a magnon). It could take a relatively a long until full alignment of electron spin along HSO.
There are many such cases. E.g. the conduction electrons in a metal. The size of a conduction electrons are relatively large. There are many conduction electrons, which simultaneously overlap each other. For this reason, the scattering between quantum states of conduction electrons are very frequent. The time between two consequent scatterings a conduction electron is very short (~ 1 ps). It is far not enough to finish even oven precession period and definitely it is not enough for the electron spin to align along HSO.
demerits:
Approximated Hamiltonian for Spin- orbit interaction |
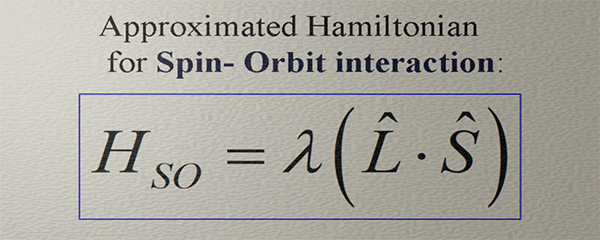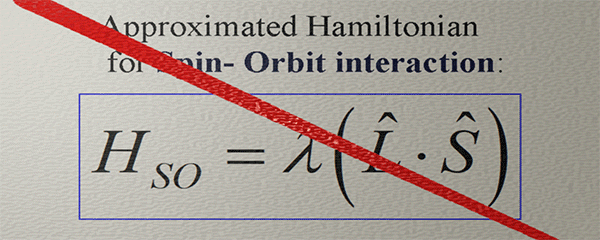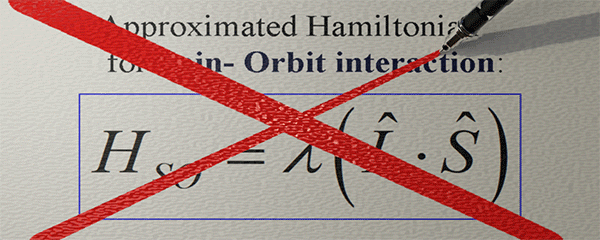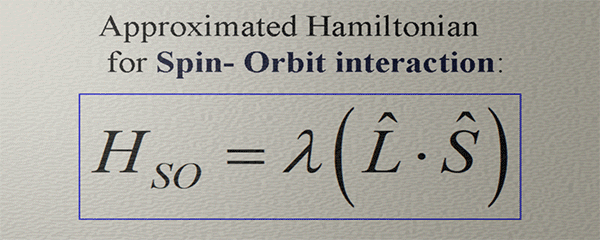 |
| (note) This Hamiltonian captures only a very general tendency that the strength and the direction of the magnetic field of the spin-orbit interaction are similar to the strength and the direction of the spin-orbit interaction. |
| The orbital moment and the magnetic field of the spin-orbit interaction do not interact directly. Instead, they align themselves in accordance with the directional and strength patterns resulting from the broken spatial and time-inverse symmetries of the electron orbital. Consequently, they exhibit similar tendencies in terms of their directions and strengths. |
| (example violation of this Hamiltonian) At an interface, the localized electrons undergo a notably potent spin-orbit interaction (See the perpendicular magnetic anisotropy (PMA)). Despite this strong SO interaction, the orbital moment of these localized electrons are fully quenched. It literally means that their orbital moment is zero. |
| click on image to enlarge it |
The classic incorrect Hamiltonian HSO of the spin-orbit interaction is just a product of the spin and the orbital of a n electron
Incorrect Hamiltonian, which only shows a general tendency:
![]()
where L is the orbital moment, S is spin, λ is the spin-orbit coupling constant
Correct Hamiltonian of Spin-orbit interaction
The effect of spin-orbit interaction describes the relativistic magnetic field HSO of a moving electrons and nothing else. As a consequence, the correct Hamiltonian is a product of the electron spin and the magnetic field of spin orbit interaction:
![]()
The spin-orbit interaction cannot break the time-inverse symmetry by itself. It requires an external magnetic to break the time-inverse symmetry. Only then the spin- orbit interaction manifests itself. As a result, the strength of the spin-orbit interaction is linearly proportional to the the total magnetic field Htotal (internal magnetic field + external magnetic field), which is applied to the electron orbital.
![]()
where kSO is the coefficient of spin-orbit interaction, which can be measured experimentally with a very high precision.
Substitution of Eq (11.4) into (11.3) gives the Hamiltonian of Spin- Orbit interaction as
![]()
where S is spin, kSO is the coefficient of spin-orbit interaction and Htotal is the total magnetic field (internal magnetic field + external magnetic field), which is applied to the electron orbital.
 |
Animated figure 6. Spin-Orbit Interaction in the center-symmetrical electrical field of atom nucleus. It is an imaginary case when electron moving in a circular orbit around nucleus (for s- symmetry electron, the orbit is spherical). Red arrow indicates the spin direction of electron. Blue arrow indicates the effective magnetic field of the spin-orbit interaction. The effective field appears only when the electron moving. The directions of the effective field is opposite for the opposite direction of the electron movement. There is a spin of precession around the effective magnetic field of the spin-orbit interaction. The electrons spin slowly aligns itself along the effective magnetic field because of the precession damping. |
![]() .....
.....![]()
-- Enhancement (magnification) of the applied magnetic field.
Due to the spin-orbit interaction, an electron experiences the effective magnetic field, which is larger than the actual applied magnetic field.
where it is the case: (1) changing of g-factor; (2) perpendicular magnetic anisotropy; (3) magnetostriction
-- Spin-dependent scatterings.
Due to the spin-orbit interaction, the scattering probability for electrons with opposite spins becomes different.
where it is the case: (1) Anomalous Hall effect; (2) Spin Hall effect
-- Spin precession. Spin relaxation.
When electron moves across a strong electrical field, the effective magnetic field of the spin-orbit interaction causes a spin precession.
where it is the case: a electrical current flowing along an interface or a junction.
When an electron may move at different angles, it may cause different directions of the precession, therefore the spin relaxation.
![]() (Effect 1) -g-factor becomes larger than g-factor of an electron in the free space ;
(Effect 1) -g-factor becomes larger than g-factor of an electron in the free space ;
![]() (Effect 2)-The bulk-type Spin Hall effect due to scatterings on non-magnetic and magnetic impurities
(Effect 2)-The bulk-type Spin Hall effect due to scatterings on non-magnetic and magnetic impurities
![]() (Effect 3)- The interface-type Spin Hall effect due to interface scatterings
(Effect 3)- The interface-type Spin Hall effect due to interface scatterings
![]() (Effect 4)- spin relaxation becomes larger. Especially for delocalized electrons (conduction electrons) of p- symmetry (-d or -f as well)
(Effect 4)- spin relaxation becomes larger. Especially for delocalized electrons (conduction electrons) of p- symmetry (-d or -f as well)
![]() (Effect 5)- saturation magnetization becomes larger (exchange interaction is enhanced due to the spin-orbit interaction)
(Effect 5)- saturation magnetization becomes larger (exchange interaction is enhanced due to the spin-orbit interaction)
![]() (Effect 6)-interface-induced perpendicular anisotropy (for example, Co/Pt). It is due to a large difference in the spin-orbit enhancement for magnetic field directed along and across the interface
(Effect 6)-interface-induced perpendicular anisotropy (for example, Co/Pt). It is due to a large difference in the spin-orbit enhancement for magnetic field directed along and across the interface
![]() (Effect 7)- changing the magnetization and magnetization direction due to the stress. Magnetostriction (magneto- elastic) effect. The stress in a metallic single-crystal multilayer structure.
(Effect 7)- changing the magnetization and magnetization direction due to the stress. Magnetostriction (magneto- elastic) effect. The stress in a metallic single-crystal multilayer structure.
![]() (Effect 8)- Anomalous Hall effect (AHE)
(Effect 8)- Anomalous Hall effect (AHE)
The Spin-Orbit interaction describes the fact that an electron experiences an effective magnetic field when it moves in an electrical field.
The effective magnetic field HSO of the Spin-Orbit interaction affects only the electron spin. Interaction of HSO with electron spin leads to
1) There can be a spin precession
2) There can be a damping of the spin precession, which aligns the electron spin along the effective magnetic field of the spin-orbit interaction
3) Electron transport can become spin-dependent
4) The electron energy becomes spin-dependent.
When a crystal consists of different atoms, the electrons are distributed asymmetrically. Some electron orbit is shifted from a cation to be closer to anion. , the orbital becomes deformed. That causes a stronger spin-orbit interaction. This is reason, for example, why the spin-orbit interaction is significantly stronger in GaAs than in Si.
In an ionic crystal the covalent electrons are nearly-fully transformed from a cation to a anion and the electron orbital becomes again more center-symmetrical with a weak spin-orbit interaction. This is reason, for example, why the spin-orbit interaction is significantly weaker in ZnO than in GaAs.
Simple answer: The strength of the spin-orbit interaction is directly proportional to the electric field of the nucleus. The nucleus charge is larger for an element of a larger atomic number. Therefore, the electrical field of the nucleus and the spin-orbit interaction, which is induced by this field, becomes larger as well.
Another reason: the screening by inner electrons becomes weaker and asymmetrical (See below)
Because of the screening of an electrical field of a nucleus by inner electrons , the strength of spin-orbit interaction reduces.
The effects of screening:
(effect 1) The spin-orbit interaction (SO), which is induced by a anion, is smaller than the SO, which is induced by a cation.
Since there are more electrons in the vicinity of an anion than in the vicinity of cation, the screening of nucleus field of anion is larger. Therefore, the spin-orbit interaction induced by the nucleus of anion is smaller.
(effect 2) In atoms of unfilled inner shells the spin-orbit interaction is stronger.
In the case when the inner shell of atom is not fully filled, the screening of the nucleus by the electrons of the inner shell is not centrosymmetric. It makes the spin-orbit interaction stronger.
The magnetic moment of an electron is a quantum- mechanical sum of magnetic moments induced by the spin and induced by the orbital moment.
Time-inverse symmetry is not broken click here to enlarge |
| Fig. 12. Electron orbital. The green arrows show the direction of the effective magnetic field of the spin-orbit interaction HSO |
Time-inverse symmetry: not broken
Average effective magnetic field of the spin-orbit interaction: zero
When the time-inverse symmetry in the material is not broken, there is an equal probability that electron circulating around the nucleus in the clockwise and anti clockwise directions. Since the electron experiences equal and opposite effective magnetic field of the spin-orbit interaction, in the average the electron does not experiences any effective magnetic field of the spin-orbit interaction. (See Fig. above)
Even in the case when the orbital moment of the electron is not zero, when the time-inverse symmetry in the material is not broken, there is an equal probability for an electron to occupy the orbit with opposite orbital moment and again the average effective magnetic field of the spin-orbit interaction: zero
note: in this case the spin-orbit interaction affects the spin relaxation
---------------------------------------------
There is no contradiction. Globally, there is no magnetic field in both cases. However, locally each atom experience a magnetic field, which is magnified by the spin-orbit interaction. The magnification is different for the orbital of a different symmetry. As a result, the orbitals experience a different HSO and the orbital energies become different. (See more details Here)
![]()

![]()

![]() How the time-inverse symmetry is broken
How the time-inverse symmetry is broken
It results: Average effective magnetic field of the spin-orbit interaction becomes non-zero
An external magnetic field breaks the time-inverse symmetry and it causes a non-zero average effective magnetic field of the spin-orbit interaction in the direction of the external magnetic field.
Since the electron moves around the nucleus, it experiences the Lorentz force in the magnetic field. The Lorentz force is in opposite directions for electron moving in the clockwise and counterclockwise directions around the magnetic field. The Lorentz force modifies the orbital of electrons. When an electron moves in the counterclockwise direction, it moves closer to the nucleus and it experiences the larger electrical field from the nucleus and the larger corresponded effective magnetic field of the the spin-orbit interaction. When an electron moves in the clockwise direction, it moves more distant from the nucleus and it experiences the smaller electrical field from the nucleus and the smaller corresponded effective magnetic field of the the spin-orbit interaction. In the average, the average the electron experiences a non-zero effective magnetic field of the the spin-orbit interaction in the direction of the external magnetic field.
Fig. 13 shows the diamagnetic response of the atom to the external magnetic field. Therefore, a material with the largest diamagnetic constant should have the largest spin-orbit interaction.
Notice: all electrons have the diamagnetic response shown in Fig. 13, including electrons of the inner orbitals and electrons of the inert gases. However, the electrons of the the external orbitals have uncompensated spin and only they experiences the spin-orbit interaction.
![]() The SO interaction is important for a large objects as well. For example, the influence of SO interaction is very strong in case of a Giant object (like a neutron star or a black hole). In the vicinity of these giant objects the particles move at near the speed of light and there is a substantial electrical field. As a result, the SO magnetic field is very strong in the vicinity of a neutron star or a black hole.
The SO interaction is important for a large objects as well. For example, the influence of SO interaction is very strong in case of a Giant object (like a neutron star or a black hole). In the vicinity of these giant objects the particles move at near the speed of light and there is a substantial electrical field. As a result, the SO magnetic field is very strong in the vicinity of a neutron star or a black hole.
![]() The Spin-Orbit interaction is a relativistic effect, but not a Quantum-Mechanical effect. The Dirac equations are relativistic quantum-mechanical equations describing the quantum field of electrons. As any relativistic equations, they contain the information about the SO interaction. Any relativistic equations, which describe the photon-electron interaction, should contain a description of the SO interaction. For example, the Maxwell's equations contain the description of the SO interaction as well.
The Spin-Orbit interaction is a relativistic effect, but not a Quantum-Mechanical effect. The Dirac equations are relativistic quantum-mechanical equations describing the quantum field of electrons. As any relativistic equations, they contain the information about the SO interaction. Any relativistic equations, which describe the photon-electron interaction, should contain a description of the SO interaction. For example, the Maxwell's equations contain the description of the SO interaction as well.
![]() Only a field of the SO interaction is the magnetic field. The SO magnetic field HSO is a very "normal" magnetic field, which is undistinguished from any other magnetic fields (e.g. the magnetic field created by an electrical current). There is only one difference between HSO and "normal" magnetic field, HSO cannot induce the Lorentz force
Only a field of the SO interaction is the magnetic field. The SO magnetic field HSO is a very "normal" magnetic field, which is undistinguished from any other magnetic fields (e.g. the magnetic field created by an electrical current). There is only one difference between HSO and "normal" magnetic field, HSO cannot induce the Lorentz force
![]() An electron experiences the SO magnetic field only in the coordinate system, which moves together with the electron. In this coordinate system, the electron does not move. It stay still. Therefore, in this coordinate system the electron does have any orbital moment or any movement-relative property and the SO magnetic field can only interact with the electron spin. The spin is only one magnetic property remaining for a motionless still object. For the same reason, the SO magnetic field does not create the Lorentz force. The Lorentz force is created when an electron moves in a magnetic field. In the coordinate system where the SO magnetic field HSO exists, the electron does not move. This property is related to the Quantum Mechanics.
An electron experiences the SO magnetic field only in the coordinate system, which moves together with the electron. In this coordinate system, the electron does not move. It stay still. Therefore, in this coordinate system the electron does have any orbital moment or any movement-relative property and the SO magnetic field can only interact with the electron spin. The spin is only one magnetic property remaining for a motionless still object. For the same reason, the SO magnetic field does not create the Lorentz force. The Lorentz force is created when an electron moves in a magnetic field. In the coordinate system where the SO magnetic field HSO exists, the electron does not move. This property is related to the Quantum Mechanics.
![]() The SO interaction is not small at all. In a ferromagnetic metal with perpendicular magnetic anisotropy (PMA), HSO may reach tens of kGauss. For example, in a thin Fe film it can override the demagnetization field of 20-30 kGauss and align the magnetization perpendicularly to the film surface.
The SO interaction is not small at all. In a ferromagnetic metal with perpendicular magnetic anisotropy (PMA), HSO may reach tens of kGauss. For example, in a thin Fe film it can override the demagnetization field of 20-30 kGauss and align the magnetization perpendicularly to the film surface.
![]() The SO interaction is not directly related to the orbital moment (see here). Even though in same specific cases, such relation can be established.
The SO interaction is not directly related to the orbital moment (see here). Even though in same specific cases, such relation can be established.
As was shown above, the strength of the spin orbit interaction substantially depends on the breaking on the orbital spatial symmetry and the time-inverse symmetry. The orbital symmetry is different for an electron of a different orbital moment. As was shown above, the dependence of the SO interaction on the orbital spatial symmetry is more rich and complex than just its dependence on its orbital moment.
Note: the formulas for orbital momentum and the spin-orbit interaction are very similar. The difference between them is only coefficient 1/r2. In close vicinity of the nucleus, the 1/r2 is huge and it makes a huge difference.
A. Yes. Even though the Schrödinger equation is not a relativistic equation, its combination with the Maxwell's equations, which are relativistic equations, gives a correct description of the SO interaction. The spin properties should be included into the solution. Such description includes the relativistic features of the electromagnetic field, but does not include the relativistic features of the quantum field of an electrons. However, for a description of effects in a solid state these features can be included by adjusting some parameters and constants.

A. Actually, not. Even though there are common tendencies between the spin-orbital interaction and the orbital moment. E.g. When orbital moment is zero, the SO interaction is zero. When orbital moment changes its sign, the SO interaction changes its sign as well.
Even though the "orbital" is a part of name of the SO interaction, the relation between orbital moment and the HSO is complex and not straightforward.
The spin-orbit interaction:

for centrosymmetric electrical field of a nucleus:
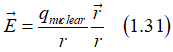
where qnucleus is the nucleus charge.
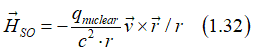
![]() HSO is proportional to ~1/r. As a result, the main contribution to HSO is from region in proximity of the nucleus. The symmetry of electron distribution function and electron rotation symmetry in close vicinity of the nucleus mainly contribute to HSO
HSO is proportional to ~1/r. As a result, the main contribution to HSO is from region in proximity of the nucleus. The symmetry of electron distribution function and electron rotation symmetry in close vicinity of the nucleus mainly contribute to HSO
The orbital moment:
![]()
or in quantum-mechanical representation
![]()
![]() L is proportional to ~r. As a result, both regions, which are close and far from the nucleus, give a substantial contributions to L.
L is proportional to ~r. As a result, both regions, which are close and far from the nucleus, give a substantial contributions to L.
Even though a formal relation between HSO and L is very simple:
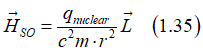
The integration over electron distribution gives very different value of HSO and L depending on the symmetry and details of electron wavefunction.
orbital momentum vs rotation symmetry |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||
|
||||||||||||
Orbitals |
||||||||||||
|
||||||||||||
|
||||||||||||
| Orbital moment | ||||||||||||
|
||||||||||||
|
||||||||||||
|
||||||||||||
| Fig.9. click on image to enlarge it |
A. It is because, for the spherical orbit an electrons makes an equal number of rotations in two opposite directions. Since for opposite rotation directions the directions of the effective magnetic field of the spin-orbit interaction are opposite, an electron does not experience any spin-orbit interaction.
No, See center and right pictures
Orbital rotation of conduction electrons |
||||
|
||||
Yellow wavy ellipse shows the wave function of the conduction electron. Blue circle show the direction of rotation of the conduction electron around each atomic nucleus (dark spheres).Electrical field of each nucleus induces the magnetic field interaction HSO. The electron experiences the accumulative strong HSO. Even though the electrons moves along stationary nuclei,accumulative HSO remains constant. |
||||
| The size of a conduction electron (size of its wave function) is relatively large. A conduction electron can cover simultaneously hundreds or thousands of nuclei. | ||||
| camera moves with the electron | ||||
| click on image to enlarge it |
The s-orbital can be divided to the sum of two spherical orbital, for which HSO is a no zero and opposite between two orbitals.
A. No, it is not correct. The spin-orbit interaction does not affect an electron of s-orbital for the following reason: An electron is an elementary particle, which could not be divided into the parts (See here). Therefore, it is impossible that the spin of one part of the electron rotates in one direction and the spin of another part rotates in a different direction. A whole electron has only one direction of the spin. In the case when along the length of electron (the mean-free path) or along the electron orbit the magnetic field changes, the spin interact with an average magnetic field. It is important there is always one defined spin direction for one electron.
quenched and unquenched orbital moments (See details here))
![]() unquenched orbital: orbital moment can be freely rotated in any direction. E.g. orbital moment can align alone an external magnetic field.
unquenched orbital: orbital moment can be freely rotated in any direction. E.g. orbital moment can align alone an external magnetic field.
![]() quenched orbital: orbital moment cannot be freely rotated. Its orbital direction either is fixed or its orbital momentum is zero.
quenched orbital: orbital moment cannot be freely rotated. Its orbital direction either is fixed or its orbital momentum is zero.
An unique spacial electron distribution each orbital moment. When the orbital moment is changed, the orbital spatial distribution is changed as well. However, the bonding of atom in a solid fixes the spacial electron distribution. The orbital moment of bonding electrons cannot be rotated. Otherwise, the bonding would be destroyed. As a result, the total orbital momentum of bonding electrons is zero.
orbital moment of electrons in a metal (common case)
localized electrons: the orbital moment is zero and orbital is quenched
conduction electrons: the orbital moment is a non-zero and orbital can be either quenched or unquenched
| orbital momentum in | |||||||||
|
|||||||||
| click on image to enlarge it |

![]() (type 2: strong SO) SO induced by external magnetic field external magnetic field
(type 2: strong SO) SO induced by external magnetic field external magnetic field![]()
![]()
Enhancement of external magnetic field |
Fig. 14. The external magnetic field Hext induces the effective magnetic field of the spin-orbit interaction HSO, which is is in the same direction as the external magnetic field.. Therefore, the total magnetic field, which the electron experiences, becomes larger. |
| note: Magnitude of HSO depends significantly on the direction, in which Hext is applied with orbit to orbital symmetry. |
| click on image to enlarge it |
(source of electrical field): centrosymmetric electrical field of atomic nucleus
(source of breaking of time-inverse symmetry): an external magnetic field
(induced effects): Perpendicular magnetic anisotropy (PMA), voltage-controlled magnetic anisotropy (VCMA)
![]() localized electrons experience this type of SO
localized electrons experience this type of SO
Explanation of effect:
The type 2 of spin-orbit interaction is induced be an external magnetic field. E.g. in absence of a external magnetic field a localized electron does not experience any HSO. However, when external magnetic field Hext is applied, it induces strong HSO parallel to Hext and the electron experiences a stronger total magnetic field Htotal =Hext+HSO. E.g. when Hext=1 kG is applied, it induces HSO.=5 kG. Therefore, in total electron experience Htotal=6 kG.
![]()
![]() Reason why an external magnetic field Hext induces the spin-orbit interaction HSO
Reason why an external magnetic field Hext induces the spin-orbit interaction HSO
(without external magnetic field): The orbital moment of the localized electrons is zero (or unquenched (See details here)). Any 3D orbital can be divided as a sum of two 2D orbitals of CCW and ACW electron rotation. Since the total moment of the localized electrons is zero, the CCW and ACW orbitals are identical. As a result, the electron experience the same but opposite HSO for the CCW and ACW orbitals , therefore in total it experiences no HSO
(with external magnetic field):Since electron rotation in the CCW and ACW orbitals is opposite, the Lorentz force is opposite for CCW and ACW orbitals. As a result, the CCW and ACW orbitals are deformed differently in an external magnetic field, HSO becomes different for CCW and ACW orbitals and in total the electron experiences a non-zero HSO.
Origin of SO interaction of type 2 |
| Without external magnetic field, a localized electron does not have any orbital moment. It means the electron rotates in CCW and ACW directions on exactly the same orbital and experiences the same, but opposite HSO. The HSO is induced by the electrical field of nucleus. Therefore, in total the electron experiences no SO, HSO=0. |
| Under external magnetic field, CCW orbital becomes slightly closer to nucleus and CCW orbital becomes more distant due to the Lorentz force FLor. As result, HSO becomes different for CCW and ACW orbitals and in total HSO becomes a non-zero |
| click on image to enlarge it |

(influence 1) ![]()
 Electron energy is changed. (less important for SO)
Electron energy is changed. (less important for SO)
The electron energy changes in a magnetic field according to its orbital moment. The orbital moment is aligned along magnetic field minimizing magnetic energy. The energy of s- electrons (orbital moment L=0) does not change. The energy of p-, d-, f- electrons (orbital moment L=1,2,3) changes.
(influence 2) ![]()
 Time- inverse symmetry is broken. (very important for SO)
Time- inverse symmetry is broken. (very important for SO)
The magnetic field changes the spacial distribution of an electron orbital, which breaks the time-inverse symmetry for the orbital. The part of electron distribution, which corresponds to the electron rotation in ACW direction with respect to magnetic field, is becomes closer to the nucleus. The part of electron distribution, which corresponds to the electron rotation in CCW direction with respect to magnetic field, is shifted away from the nucleus.
Note: The breaking of the time - inverse symmetry of the orbital does not depend whether the electron energy or electron orbital moment is changed or not. For example, a magnetic field breaks the time- inverse symmetry even for the s-orbital, even though the magnetic field does not change either energy or orbital moment of the s- orbital.
Magnetic field, which applied to electron orbital, creates additional magnetic field due to the spin- orbit interaction. As a result, the electron spin interacts with a larger magnetic field than externally applied. |
|
| Magnetic anisotropy is due to this effect. See Perpendicular magnetic anisotropy |
| Measurement of the strength of spin- orbit interaction is based on this effect (See below) |
 When an external magnetic field is applied, the spin-orbit interaction induces an additional magnetic field along the same direction. As a result, electrons experience a combined magnetic field that is larger than the externally applied field, primarily due to the presence of the spin-orbit interaction.
When an external magnetic field is applied, the spin-orbit interaction induces an additional magnetic field along the same direction. As a result, electrons experience a combined magnetic field that is larger than the externally applied field, primarily due to the presence of the spin-orbit interaction.In fact, it is the joint work of two relativistic effects: 1) the Lorentz force 2) the spin-orbit interaction
- The Lorentz force, which is induced by an external magnetic field, deforms the electron orbital and breaks the time-inverse symmetry;
- Because of the broken time-inverse symmetry, the strong effective magnetic field is induced by the spin-orbit interaction.
(key property of spin- orbit interaction): |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||
| This feature of the spin-orbit interaction originates the perpendicular magnetic anisotropy (PMA). See here for details. | |||||||||||||||
| click on image to enlarge it |
 (origin of the effect):
(origin of the effect):
Time-inverse symmetry is broken click here to enlarge |
| Fig. 13. Electron orbital in the presence of external magnetic field (blue arrow). The green arrows show the direction of the effective magnetic field of the spin-orbit interaction HSO The red arrows show the direction the Lorentz force |
The part of the orbital that rotates clockwise around the magnetic field contracts due to the Lorentz force, bringing it closer to the nucleus, where the electric field is stronger. Consequently, this portion of the orbital experiences a greater spin-orbit magnetic field.
Conversely, the counterclockwise rotating portion of the orbital expands and moves away from the nucleus, resulting in a smaller spin-orbit magnetic field.
Since the electric field diminishes with increasing distance from the nucleus following a 1/r decay, the gain from the clockwise rotating component surpasses the loss from the counterclockwise rotating component. As a result, the electron experiences an overall amplified magnetic field due to the spin-orbit interaction.
(key property 2 of spin-orbit interaction): |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
| (note: simplified schematic): |
|||||||||
| (note about PMA) |
|||||||||
| (note about atomic neighbors) |
|||||||||
| (note interface and bulk) |
|||||||||
| click on image to enlarge it |
The increase of the effective magnetic field due to the spin orbit interaction |
Fig. 14. The external magnetic field Hext induces the effective magnetic field of the spin-orbit interaction HSO, which is is in the same direction as the external magnetic field.. Therefore, the total magnetic field, which the electron experiences, becomes larger. |
| click on image to enlarge it |
When a magnetic applied to the material, it breaks the time inverse symmetry. As result, the electron starts to experience non-zero effective field of the spin-orbit interaction.
The effective magnetic field HSO of the spin-orbit interaction is in the same direction as the applied external magnetic field.
The total magnetic field, which the electron experiences, becomes larger. In some cases, the total effective magnetic field may be a significantly larger than the external magnetic field.
The induced effective magnetic field of the spin-orbit interaction may be significantly different for different directions of the applied external magnetic field. It is the largest in the direction, in which the electron orbit is deformed (See Fig. 14).
The increase of the spin-orbit interaction due to deformation of the electron orbital click here or on image to enlarge it |
| Fig. 9. Electron orbital. When the orbital is spherical the effective magnetic field of the spin-orbit interaction HSO is zero. Only when the orbital is deformed, there is the magnetic field of the spin-orbit interaction. The effective magnetic field is the largest in the case of a circle or elliptical orbital. |
The type of orbit deformation, which may enlarge the spin-orbit interaction
![]() (1) The electron orbit should be deformed along one direction
(1) The electron orbit should be deformed along one direction
![]() (2) The electron orbit should be deformed asymmetrically in respect to its nucleus
(2) The electron orbit should be deformed asymmetrically in respect to its nucleus
The orbital is significantly deformed in compound materials with covalent bonding (like GaAs). Therefore, they have a larger spin-orbit interaction.
In materials with ionic bonding, the orbital is less deformed and they have a smaller spin-orbit interaction (like ZnO).
The p- , d- and f- orbitals are inherently asymmetrical. For each individual p- , d- and f- orbital, the spin-orbit interaction may be strong.
For each individual p- or d- or f- orbital, the time-inverse symmetry is broken. However, in a non-magnetic metal or a semiconductor, where the time-inverse symmetry is not broken, the electron wavefunction is a combination of the wave functions of different moments and it is more symmetric. Therefore, in a crystal the spin-orbit interaction of electrons of p- or d- or f- symmetry may be not as strong as in the case of a separated atom.
Increase of spin-orbit interaction due to crystal deformation. |
| Fig. 20. Due to the crystal deformation, the orbital are deformed and the nuclei are shifted out of the center of the orbital. It makes HSO (green arrow) larger and the magnetic energy larger. |
| Green arrows show the effective magnetic field HSO of the spin-orbit interaction. It is large only when the orbitals are deformed. |
| Blue arrows show the intrinsic magnetic field Hinside. It the total magnetic field, which electron experience: external magnetic field, magnetic field from neighbor orbitals. The total magnetic field except HSO |
| White spheres show the orbitals of the localized d-electrons |
|
When a pressure applied to the film, the atomic orbitals are deformed. There are two types of deformations. (type 1): The orbital becomes more elliptical. (type 2): nuclei are shifted out of the center of the orbital. Both deformation makes the effective magnetic field HSO of the spin-orbit interaction larger.
In a ferromagnetic material the localized electrons have a non-compensated spin, which creates a magnetic field Hmag
At an interface between a magnetic and non-magnetic material, the demagnetization field Hdemag is created due to uncompensated magnetic moment at the interface. The direction of Hdemag is perpendicular to the interface and opposite to Hmag.
The magnetic field Hinside inside of the ferromagnetic field equals Hmag- Hdemag. The Hinside is the total magnetic field except HSO. It includes the external magnetic field
![]() Important fact: Additionally, the electron experience the effective magnetic field HSO of the spin-orbit interaction, which is always directed along Hinside. The magnitude of HSO is proportional to Hinside and the degree of the orbital deformation.
Important fact: Additionally, the electron experience the effective magnetic field HSO of the spin-orbit interaction, which is always directed along Hinside. The magnitude of HSO is proportional to Hinside and the degree of the orbital deformation.
![]() Without a deformation the orbitals of the localized electrons is nearly spherical and the effective magnetic field HSO of the spin-orbit interaction is small.
Without a deformation the orbitals of the localized electrons is nearly spherical and the effective magnetic field HSO of the spin-orbit interaction is small.
![]() When the pressure applied, the orbitals are deforms in the direction of the applied pressure and the effective magnetic field HSO of the spin-orbit interaction increases.
When the pressure applied, the orbitals are deforms in the direction of the applied pressure and the effective magnetic field HSO of the spin-orbit interaction increases.
The magnetic energy of an electron equals to a product of the electron spin and Hinside+HSO.
When magnetization is perpendicular to the film, the orbital deformation is larger, HSO is larger and the magnetic energy is larger.
When magnetization is in-plane, the orbital deformation is smaller, HSO is smaller and the magnetic energy is smaller.
The dependence of the magnetic energy on the magnetization direction is called the magnetic anisotropy. In the case when the difference of the magnetic energy are with respect to the interface, the effect is called the perpendicular magnetic anisotropy (PMA)

This type of spin- orbit interaction is the origi
SO interaction induced by an electrical current. Spin Hall effect |
 |
Fig.2 (left) 2D scan of Kerr rotation angle θKerr in GaAs 30-um-wide wire. θKerr is proportional to number of spin-polarized electrons nS , when an electrical current flows through the wire. T=30 K; (right) top- view optical optical image of same GaAs wire |
The red and blue regions at wire side are regions of spin accumulation. Red and blue colors corresponds to spin-up and spin-down directions of spin accumulation. White color corresponds to regions without any spin accumulation. |
Y. K. Kato, R. C. Myers, A. C. Gossard, D. D. Awschalom, "Observation of the Spin Hall Effect in Semiconductors". Science 306, 1910-1913 (2004) |
click on image to enlarge it. See details here |
![]() (type 3: spin- orbit interaction due to electrical current) creation of spin polarization by an electrical current
(type 3: spin- orbit interaction due to electrical current) creation of spin polarization by an electrical current![]()
![]()
![]()
(source of electrical field): centrosymmetric electrical field of atomic nucleus
(source of breaking of time-inverse symmetry): an electrical current
(induced effects):Spin Hall effect & Inverse Spin Hall effect (main contribution), Spin-Orbit Torque
![]() Only conduction electrons experience this type of SO
Only conduction electrons experience this type of SO
Explanation of the effect:
(effect 1): ![]() Spin Hall effect
Spin Hall effect
When electrical current flows in a metallic wire, it generates a spin current flowing perpendicularly to the electrical current
(effect 2):![]() Spin pumping
Spin pumping
When electrical current flows in a metallic wire, it creates spin-polarized conduction electrons. As a result, initially spin-unpolarized gas of conduction electrons becomes spin-polarized.
(effect 3):![]() Inverse Spin Hall effect (ISHE)
Inverse Spin Hall effect (ISHE)
When a spin-polarized current flows in a metallic wire, it generates a charge current (conventional current)flowing perpendicularly to the spin current.
(effect 4):![]() Spin damping
Spin damping
When the electron gas is spin-polarized, there are spin-polarized conduction electrons, which spins is directed in one direction. When the conduction electron has a non-zero rotational (orbital) moment, it experiences a non-zero HSO and there is a spin precession around HSO. Since the direction of HSO is different for electrons moving in different directions, the spin precession is along different directions for electrons moving in different directions. As a result, the spins of spin-polarized electrons is misaligned from one direction and degree of the spin polarization is reduced.
Spin Hall effect due to a non-zero orbital moment of conduction electrons induced by an electrical current J |
|||||||||
|
|||||||||
Fig. 3. Distribution of electrons with orbital moment and distribution of HSO. |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| The length of a vector from axis origin to the sphere is proportional to the number of electrons moving in the vector direction. Red arrow shows the direction of electron movement. Blue circle shows the direction of orbital moment. Violet arrow shows direction of HSO induced by the orbital moment. The direction of orbital moment and HSO is fixed to the electron movement direction. | |||||||||
|
|||||||||
|
|||||||||
|
|||||||||
| Each election moving in a different direction experiences magnetic field HSO in a different direction. | |||||||||
| When a conduction electron moves along crystal lattice, it simultaneously rotates around each atomic nucleus as it passes it. The electrical field of nucleus induces the magnetic field of spin-orbit interaction. The spin of conduction electrons interacts with HSO. There is a spin precession around HSO and spin precession damping, which aligns spin to HSO. | |||||||||
| click on image to enlarge it. See details about this contribution to spin Hall effect here |
there are two contributions ![]() to current-induced spin-orbit effects:
to current-induced spin-orbit effects:
Spin Hall effect of type 1 |
due to electron movement perpendicularly to electrical field (Schottky- type) at interface |
|---|
Fig. 30 . The electron current in a GaAs stripe. The view point moves together with electrons. Because of the charge depletion at the GaAs-oxide boundary, there is an electrical filed E perpendicular to the boundary (shown as the green arrows). The electrical field E induces the effective magnetic field HSO of the spin-orbit interaction (red arrows). The direction of the effective magnetic field is opposite at the opposite sides of the GaAs strip. Spins of conduction electrons is aligning along HSO. As a result, the conduction electrons becomes spin- polarized. The direction of the spin- polarization is along HSO |
| When the conduction electrons moved near the edge of the GaAs strip, the spins precess around the magnetic field HSO. Because the damping of the spin precession the spins are aligned along the effective magnetic field of the spin-orbit interaction. |
| The electrical field, HSO and spin polarization exponentially decays from the interface deep into the wire. There are no E, HSO and spin polarization at the center of the wire. |
| Due to the Schottky barrier at the boundary, the electrons are depleted (accumulated) at the boundary region creating the electrical field E. |
| click on image to enlarge it |
(contribution 1) ![]() band current
band current 



![]() (explanation of effect):
(explanation of effect):
(step 1) The conduction electron have a non-zero rotational (orbital) moment,which created magnetic field HSO. There is a spin precession around HSO and the spin is aligning along HSO due to the damping of the spin precession.
(step 2) When there is no electrical current, there are equal numbers of electrons moving in any two opposite directions. Since the rotational (orbital) moment and HSO are equal and opposite for electrons moving in opposite direction, both the total rotational (orbital) moment and total are zero for the electron gas and scattering probabilities are independent on electron movent direction and electron spin
(step 3) When there is an electrical current, the number of conduction electrons moving along current is larger than number of electrons moving in the opposite direction. As a result, the rotational (orbital) moment of electrons moving along current is not fully balanced by the opposite moment of electrons moving in the opposite direction and the total the electron gas experience a non-zero HSO and the electron gas becomes spin-polarized.
(step 4) When there is an electrical current, the scattering probability of spin-up electrons to the left becomes different from the scattering probability to the right. As a result, e.g. the spin-up polarized current flows to the left and the spin-down polarized current flows to the right.
Distribution of conduction electrons with orbital moment |
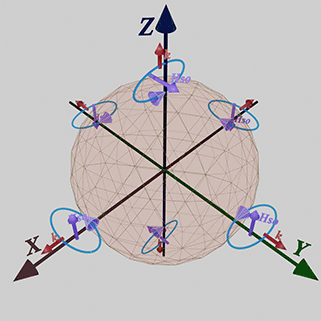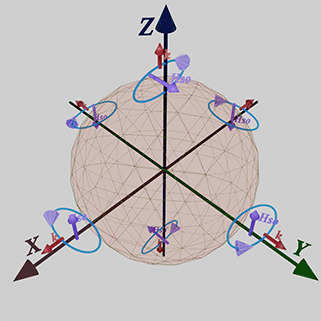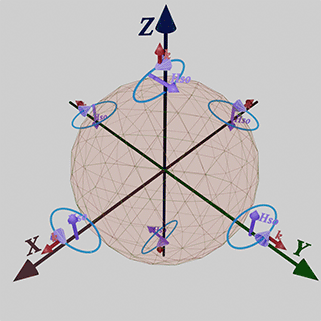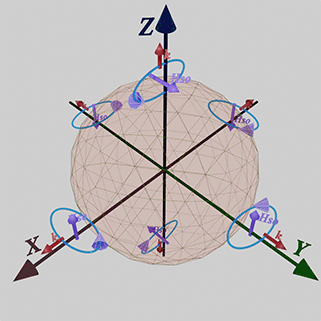 |
Fig. |
| click on image to enlarge it |
(contribution 2) ![]() scattering current
scattering current
It is a feature of a metal of a low conductivity (See here)
![]() (explanation of effect):
(explanation of effect):
(step 1) There is an electrical field in close vicinity of a defect in a metal and an interface between two metal or at edge of a metal wire. The conduction electrons are screening any electrical field in a metal. However, in close proximity of a defect or interface the electrical field is not fully screened. Especially it is the case of a metal of a low conductivity
(step 2) When a conduction electron moves along the electrical field of the defect or interface, it experience HSO and its spin is aligned along HSO
(step 3) Since direction of the electrical field is opposite from left and right sides
The conduction electrons move simultaneously in the forward direction along lattice and around each atom (nucleus) of the lattice.
Movement of a conduction electron in a metal Simultaneously with movement along the crystal a conduction electron rotates around each nucleus. The rotation and the linear movent cause two different types of the spin-orbit interaction. |
 |
Spin relaxation due to non-zero orbital moment of a conduction electron |
||||||||||||
|
||||||||||||
|
||||||||||||
| click on image to enlarge it |


(Mechanism): The incoherent spin precession around HSO
The spins of all spin- polarized electrons are directed in one direction. In contrast, the direction of HSO is different for electrons moving in different directions. As a result, the angle between electron spin and HSO is different for the spin- polarized electrons moving in different directions. There is a spin precession around HSO. Since the directions of HSO are different for conduction electrons moving in different directions, their precession directions are different as well. The precession in different directions misaligns spins of spin- polarized electrons, which causes the spin relaxation.
A. Additionally to the mechanism of the spin misalignment (mechanisms of the spin relaxation), there are mechanisms, which align all spins in one direction (mechanism of the spin pumping). The simple electron scatterings are most efficient as a spin alignment mechanisms. The symmetry- and spin- feature of electron scatterings is that they redistribute randomly spin- misaligned group of conduction electrons into a group of spin- polarized electrons, in which all spins are aligned in one direction, and the group of spin- unpolarized electrons, in which spins are distributed equally in all directions. See here more details about scatterings and spin distributions.
Spin relaxation |
|||||
Spin relaxation is a joint work of (1) spin misalignment due to spin precession around HSO and (2) scatterings |
|||||
|---|---|---|---|---|---|
|
|||||
| The direction of vector from axis origin to the pink sphere corresponds to the electron movement direction. The length of a vector from axis origin to sphere is proportional to the number of electrons moving in the vector direction. The blue arrows show the direction of . The direction of is different for electron moving in different directions. The green balls shows the spin direction of spin- polarized conduction electrons. The size of the green balls is proportional to the number of the spin- polarized electrons | |||||
| click on image to enlarge it |
(video): |
|||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||||||||||||||
| click on image to play it |
In the of paramagnetic metals, the spin-orbit interaction does not produced any additional magnetic field or magnetization inside material. It only makes larger the effective magnetic field, which the electron experiences.
Note: Both the magnetic susceptibility and the spin-orbit interaction enhance the effective magnetic field, which an electron experiences. Except ferromagnetic metals, the enhancement due to the magnetic susceptibility is much weaker than the enhancement due to the spin-orbit interaction. For example (See above), in diamagnetic materials the enhancement is only about -0.001 %, in paramagnetic it is 0.01 %. As can be evaluated from the g-factor, the enhancement due to the spin-orbit interaction is 1-10 % for the most of materials. In the case of III-V semiconductors (GaAs,InAs), the enhancement may be more than 100 %.
Perpendicular-to-plane magnetic anisotropy at a Fe/Pt interface |
||||
|
||||
| Fig.15. Schematic diagram of Pt/Fe interface. The blue and red spheres show the electron orbitals in Fe and Co, respectively. Blue arrows shows the magnetization (spin of localized d-electrons). The green arrows show the effective magnetic field HSO of the spin-orbit interaction. The orbital of the localized electrons are shown. |
The magnetization of a single-material ferromagnetic film is in - plane. In the case when the film consists of a thin layers of different metals, the magnetization could be out of plane. The example of such multi-layered films are Co/Pt, Fe(fcc)/Pt, Co/Tb, Fe(fcc)/Tb.
Since the strength of the spin-orbit interaction depends of the shape of the electron orbit in a crystal, the perpendicular-to-plane magnetic anisotropy only a feature of a specific crystal orientation and only a specific crystal orientations of the interfaces. For example, in all above-mentioned cases the perpendicular-to-plane magnetic anisotropy is feature of only fcc(111) interfaces or very similar hcp interfaces
Perpendicular-to-plane magnetic anisotropy occurs due to a strong effective magnetic field of the spin-orbit interaction at the interface . The enhancement of the effective field of the spin-orbit interaction occurs because of a deformation of the orbital of the ferromagnetic and non-magnetic metals in the close vicinity of the interface.
In the bulk of the metals, the shape of the orbitals are close to a sphere (shown as the red and blue-colored spheres). In the vicinity of the contact, the orbitals are deformed.
Thickness-dependence of PMA |
||||
|
||||
Fig.16. Magnetization of CoFeB film grown on MgO. The magnetization of a thick film (thickness >1.5 nm) is in-plane , but the magnetization of a thinner film is perpendicular-to-plane |
It should be noticed that the magnetizations of a thin Fe(bcc)(001) on Cu(bcc)(001), on Ta (001), on W(100) is also is perpendicular to plane.
Since the strength of the spin-orbit interaction depends of the shape of the electron orbit in a crystal, the perpendicular-to-plane magnetic anisotropy only a feature of a specific crystal orientation and only a specific crystal orientations of the interfaces.
For example, the magnetization of a thin Co(hcp) or Co (fcc) film on MgO or on Cu is in-plane.
Increase of spin-orbit interaction due to crystal deformation. |
| Fig. 20. Due to the crystal deformation, the orbital are deformed and the nuclei are shifted out of the center of the orbital. It makes HSO (green arrow) larger and the magnetic energy larger. |
| Green arrows show the effective magnetic field HSO of the spin-orbit interaction |
| Blue arrows show the intrinsic magnetic field Hinside |
| White spheres show the orbitals of the localized d-electrons |
|
When a pressure applied to the film, the atomic orbitals are deformed. There are two types of deformations. (type 1): The orbital becomes more elliptical. (type 2): nuclei are shifted out of the center of the orbital. Both deformation makes the effective magnetic field HSO of the spin-orbit interaction larger.
Without a deformation the orbitals of the localized electrons is nearly spherical and the effective magnetic field HSO of the spin-orbit interaction is small.
When the pressure applied, the orbitals are deforms in the direction of the applied pressure and the effective magnetic field HSO of the spin-orbit interaction increases.
In a ferromagnetic material the localized electrons have a non-compensated spin, which creates a magnetic field Hmag
At an interface between a magnetic and non-magnetic material, the demagnetization field Hdemag is created due to uncompensated magnetic moment at the interface. The direction of Hdemag is perpendicular to the interface and opposite to Hmag.
The magnetic field Hinside inside of the ferromagnetic field equals Hmag- Hdemag
Additionally, the electron experience the effective magnetic field HSO of the spin-orbit interaction, which is always directed along Hinside. The magnitude of HSO is proportional to Hinside and the degree of the orbital deformation.
The magnetic energy of an electron equals to a product of the electron spin and Hinside+HSO.
When magnetization is perpendicular to the film, the orbital deformation is larger, HSO is larger and the magnetic energy is larger.
When magnetization is in-plane, the orbital deformation is smaller, HSO is smaller and the magnetic energy is smaller.
The dependence of the magnetic energy on the magnetization direction is called the magnetic anisotropy. In the case when the difference of the magnetic energy are with respect to the interface, the effect is called the perpendicular magnetic anisotropy (PMA)
bulk
MgO lattice constant a = 4.212Å (a/2=2.106Å)
Fe (BCC) lattice constant a = 2.870Å (along [110] 2.03 Å )
Case of MgO (1.8nm) on Fe (See Yuasa et al. Nature Material (2004))
MgO
Even the is much less than the critical thickness, the 2/3 of strains is relaxed (from 3.74% to 1.2 % (2.54% of strains are relaxed))
experiment:
the lattice spacing is elongated along the [001] axis by 5% and is compressed along the [100] axis by 1.2% compared with the lattice of bulk MgO (compressive stress 3 GPa . It is larger than compressive Strength of 1.6 GPa).
Fe
tensile strained (max 2.54%)
experiment
the lattice of the top Fe electrode is expanded by 1.9% along the [110] axis, which means that 0.64% is relaxed. (2.54%-1.9%)
tensile stress is 4 GPa
Example 4 Ta on Fe
The lattice constant of Ta is 13 % larger than lattice constant of Fe.
Ta is compressively strained. A thin Ta can be used with tensile-strained Fe in order to reduce the strain field and to increase the critical thickness of the tensile-strained Fe.
Magnetostriction
The mechanical stress σ can be calculated
![]()
where ε is the total strain, E is the Young’s modulus at magnetic saturation and λ is the magneto elastic strain
Enhancement of the spin-orbit interaction due to electrically induced orbital polarization |
||||
|
||||
Fig.17. The yellow mesh shows the electron orbital; the blue arrow shows direction and magnitude of external magnetic field; the green arrow shows direction and magnitude of the effective field of the spin-orbit interaction; the red arrows shows direction and magnitude of the applied electrical field; the oval at left- bottom corner shows the induced dipole polarization of the orbital. |
The external magnetic field induces the magnetic field along its direction. In the case of near-spherical orbit (Fig. 17), the enhancement is small and the magnetic field of the spin-orbit interaction is small.
In the external electrical field the positively-charged nucleus moves a little toward the direction of the electrical field. The negatively-charged electrons move in the opposite direction.
Without the electrical field the charge was symmetrically distributed (Fig. 17 left). When the electrical field is applied there is more positive charge at right side and there is more negative charge at the left side. Therefore, the electrical field induces a dipole polarization in the material. The dipole polarization is described by permittivity of the material.
Also, the magnetic field of the spin-orbit interaction becomes larger. Under the electrical field the electron orbit is deformed so that at the left side the electron distribution becomes denser in the close vicinity of the nucleus. Therefore, at the left side of the nucleus the electron experiences a larger electrical field and a larger corresponded magnetic field of the spin-orbit interaction. Even at the right side of the nucleus the spin-orbit interaction is reduced, in total the spin-orbit interaction becomes larger in the electrical field. It is because the electrical field of nucleus decays as 1/r^2 and at left side it increases sharply, but at the right the decrease is small.
![]() The spin-orbit interaction by itself cannot break the time inverse-symmetry!
The spin-orbit interaction by itself cannot break the time inverse-symmetry!
Enhancement of the spin-orbit interaction due to electrically induced orbital polarization click here or on image to enlarge it |
Fig. |
Fine structure |
 |
| The fine spliting of the energy levels of a hydrogen atom. The fine structure correction predicts that the Lyman-alpha line (emitted in a transition from n=2 to n=1) must split into a doublet. |
| Image taken from here. click on image to enlarge it |
![]() Two effects: (1) the fine structure and (2) the difference between energies of heavy and light holes) exists due to the spin orbit interaction. In both cases there is no external magnetic field, but there is a substantial spin-orbit interaction. Why?
Two effects: (1) the fine structure and (2) the difference between energies of heavy and light holes) exists due to the spin orbit interaction. In both cases there is no external magnetic field, but there is a substantial spin-orbit interaction. Why?
There is no contradiction. Globally, there is no magnetic field in both cases. However, when the orbital moment of an atom is a non-zero, locally the time-inverse-symmetry is broken for each atom and each atom experiences a magnetic field HSO of the spin-orbit interaction. Since the directions of the orbital moments are equally distributed in all directions, the gas is non-magnetic and globally there is no breaking of the time-inverse symmetry. Still changes the electron energy and there is a difference of electron energies of electrons of different orbital moments.
Difference between Global and Local breaking of the time-inverse symmetry (TIS)
It can be understood from the following example, which describes the Zeeman splitting of a gas of atoms in a magnetic field and in which the more complex effect of the spin-orbit interaction is not involved. Let us consider a gas of atoms. Each atom has a magnetic moment and a non-zero spin. Both the local and global breaking of TIS lead to the energy splitting. However, only the global breaking creates the directional- dependency of gas or material properties.
(global symmetry breaking): The symmetry is broken globally, when a sufficiently-strong external magnetic field is applied. As a result, the magnetic moment of all atoms is aligned along the magnetic field. The magnetic field field breaks the time-inverse symmetry. It results in two changes. The first change the energy of electrons with spins along and opposite the magnetic field becomes different. As a result, one energy level splits into two levels. The second result of the time-inverse symmetry breaking is that the properties of the atomic gas become direction- dependent. E.g. left- and right- circular polarized light is absorbed differently, when light propagates along the magnetic field and the absorption is the same when the light propagates perpendicularly to the field.
(local symmetry breaking): The symmetry is broken locally, but not globally, when there is a magnetic field in each atom along the atom magnetic moment, but the magnetic moments of all atoms are not aligned. It is the case when there is no external magnetic field and the magnetic moments of atoms of the gas are distributed equally in all directions. In this case there is no any directional asymmetry, but the energy splitting still remains. Each atom has the equal energy splitting independently on direction of its magnetic moment. Even though globally there is no magnetic field, the atoms of the gas experiences the Zeeman splitting.
Spin-orbit interaction makes properties of light and heavy holes different |
 |
| The the light and heavy holes experience a different magnitude of the spin-orbit interaction, due to the different symmetry of their the spacial distribution. The spin-orbit interaction causes the difference of properties between the light and heavy holes. |
| click on image to enlarge it |
It describes the fact that in the hydrogen gas the p- energy level is splits in two levels: the lower-energy level (J=1/2) and the higher-energy level (J=3/2).(More details see here)
(The reason of the energy splitting:) ![]() The orbital moment of a p- electron is non-zero. As a result, the p- electron experiences the additional spin-orbit magnetic field HSO and corresponding additional energy ESO=HSO*S, where S is the electron spin. HSO depends on the spacial symmetry of the orbital. The spacial symmetry of the orbitals of J=1/2 and J=3/2 are different. As a result, the electrons experience a different HSO and have a different energies.
The orbital moment of a p- electron is non-zero. As a result, the p- electron experiences the additional spin-orbit magnetic field HSO and corresponding additional energy ESO=HSO*S, where S is the electron spin. HSO depends on the spacial symmetry of the orbital. The spacial symmetry of the orbitals of J=1/2 and J=3/2 are different. As a result, the electrons experience a different HSO and have a different energies.
In a molecular or atomic gas, all values of the orbital moment, HSO and electron spin are non-zero. The orbital moment, HSO and electron spin are directed in one direction specific for each individual atom. Each atoms creates a dipole magnetic field around itself and theretofore it can be considered as a tiny magnet. However, the atomic gas in total is not magnetic. It is because the directions of the orbital moments, HSO and spins are equally distributed in all direction. Still HSO changes the energy of each atom, which is independent on the direction of magnetic moment of each atoms and remains as a feature of the whole gas. The dependence of HSO on the orbital moment (orbital symmetry) causes the fine energy splitting.
In a semiconductor, the holes have p- spacial symmetry. The holes are divided into two classes: the light (J=1/2) and heavy (J=3/2) holes.
(reason of difference between light and heavy holes) ![]() The the light and heavy holes experience a different magnitude of the spin-orbit interaction, due to their different orbital symmetry (orbital moment). The spin-orbit interaction causes the difference of energies (properties) between the light and heavy holes.
The the light and heavy holes experience a different magnitude of the spin-orbit interaction, due to their different orbital symmetry (orbital moment). The spin-orbit interaction causes the difference of energies (properties) between the light and heavy holes.
The orbital moment of a hole is non-zero. As a result, the hole experiences the spin-orbit magnetic field HSO and corresponding additional energy ESO=HSO*S, where S is the electron spin. HSO depends on the spacial symmetry of the orbital. The spacial symmetry of a light hole (J=1/2) and a heavy hole (J=3/2 ) are different. As a result, the the light and heavy holes experience a different HSO and have a different energies.
3 types of magnetic field |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||
| The spin properties of electrons are exactly the same for each type of the magnetic field. In an equilibrium the electron spin is aligned along the total magnetic field, which is a vector sum of all three types of the magnetic field. There is a spin precession before the alignment. | ||||||||||||
| click on image to enlarge it |
Dynamo effect |
 |
In contrast, the production of fakes in a larger numbers is much easier |
| Click on image to enlarge it |
The result of the both effect is absolutely identical. Both effects, the spin- orbit interaction and the dynamo effect, amplify an externally applied magnetic field. When a weak magnetic field is applied, the dynamo effect or the spin-orbit interaction creates much stronger magnetic field (10 times stronger or more) parallel to the the external magnetic field.
 Dynamo effect creates:
Dynamo effect creates:(result 1 of dynamo effect): Earth magnetic field ~0.5 Gauss
(result 2 of dynamo effect): Sun magnetic field ~1 Gauss
(result 3 of dynamo effect): magnetic field of a Sun dark spot ~4000 Gauss
(result 4 of dynamo effect): magnetic field of a neutron star millions of Gauss
A. Due to its relativistic nature, the spin-orbit interaction manifests itself only when the time-reversal symmetry (T-symmetry) of an electron orbital is broken. However, the spin-orbit interaction itself cannot break the T-symmetry—it necessitates an external T-symmetry-breaking factor. This only occurs when the electron is subjected to conditions where T-symmetry is already broken. There are a limited number of scenarios where this occurs: (1) in the presence of an electrical current, (2) when the electron possesses a nonzero orbital moment due to its non-quenched state, and (3) when an external magnetic field is applied. It's noteworthy that the intrinsic magnetic field within a ferromagnetic or antiferromagnetic material is regarded as an external field. Consequently, the necessity of a broken T-symmetry for the spin-orbit interaction's existence already clarifies why its strength is proportional to the external magnetic field.
While slightly oversimplified, the following provides a very illustrative explanation: Consider a fully quenched electron orbital under an external field. This scenario closely resembles the behavior of a localized d- electron in materials such as Fe or Co, which are nearly fully quenched, as indicated by FMR (Ferromagnetic Resonance). Full quenching implies that the orbital moment is zero, and the electron wavefunction can be divided into two components corresponding to clockwise and counterclockwise movements. In the absence of the orbital moment and external magnetic field, these two components experience equal but opposite magnetic fields of spin-orbit interaction. Consequently, these contributions balance each other, resulting in the electron experiencing no net spin-orbit interaction. This is the case when T-symmetry is unbroken for the orbital movement. Reversing the flow direction of time implies an exchange between clockwise and counterclockwise movement paths, which, in this case, doesn't alter anything. For spin-orbit interaction to exist, there must be a distinction between clockwise and counterclockwise rotations, indicating the breaking of T-symmetry. This symmetry can be externally broken by applying a magnetic field, which creates the Lorentz force. The Lorentz force affects the electron differently along its clockwise and counterclockwise paths. The force pushes the clockwise-rotating part of the electron wavefunction away from the nucleus while drawing the counterclockwise-rotating part closer to it. This creates a disparity in the electric field of nucleus experienced by the electron for these two opposite rotations. As a result, the equilibrium between opposing magnetic fields of spin-orbit interaction is disrupted, leading to a significant magnetic field of spin- orbit interaction experienced by the electron.
A. There are several reasons why:
(reason 1): In the case of a deformed orbital, the electron distribution become more close to the atomic nucleus (at least some of the distribution). In order for the SO be large, the electron should move in a very large electrical field, which is only exists in a very close proximity of the nucleus. Only this region mainly contributes to SO. If the ionic or atomic radius (see here or here) is about 50-100 pm, the region with radius only 1-2 pm contributes about 99% to SO (number might be slight different from case to case due to the symmetry and frequent cancelation of SO in the proximity of the nucleus).Usually a deformation of orbital moves electron (electron distribution) closer to the nucleus, which makes the SO larger.
(reason 2): In the case when the orbital moment is zero, the SO is zero, because it has two opposite contributions, which of compensate and cancel each other(see here). The deformation makes the orbital moment larger. There is no balance between two opposite contributions and the SO is enlarged. The localized electrons and the conduction electrons of the s- symmetry (e.g. n-type electrons in a semiconductor) have zero orbital moment.
(reason 3): The SO is enhanced by an external magnetic field, because of the symmetry breaking due to the Lorentz force induced by the external magnetic field. This enhancement is more efficient for less symmetrical orbital.
A. You are right. An external magnetic field enhances the SO in the case of the spherical orbital as well. However, the enhancement is more efficient for a deformed orbital than for a spherical orbital. This can be understood as follows. A deformed orbital has some part of electron distribution, which is very close to the nucleus.
A. The spin-orbit interaction is relativistic effect (it is not a quantum- mechanical effect). All effects due to the spin- orbit interaction exist for both a small object (which should be described by a wave- function) and a large object ( which can be approximated as a point- like classical object).
A. The spin- orbit interaction is a relativistic effect, which just describes the transformation of the electromagnetic field between coordinate systems moving with different speeds (Also, it describes the transformation of the quantum field of electron between different coordinate systems (See Dirac Eq.)). If the time- inverse symmetry is not broken in one coordinate system, it is not broken in any other coordinate system. It doesn't matter whether the coordinate system is moving or not. It is the reason why the spin- orbit interaction cannot break the time- inverse symmetry. In order to manifest itself, the spin- orbit interaction always requires an external breaking of the time- inverse symmetry.
A.(time- inverse symmetry & electrical current) ![]() An electrical current is always breaking the time inverse symmetry. The reversal of time makes the electrons to move in the opposite direction. The time -inverse symmetry is broken for any material property, which depends on the direction of electron movements or the polarity of the current.
An electrical current is always breaking the time inverse symmetry. The reversal of time makes the electrons to move in the opposite direction. The time -inverse symmetry is broken for any material property, which depends on the direction of electron movements or the polarity of the current.
(weak SO & breaking of time- inverse symmetry)  It is the basic relativistic SO, which describes the fact that an electron is experiences a magnetic field when it moves perpendicularly to an electrical field. This effect can be understood as following. The electrical field is only one specific case of the more general electromagnetic (EM) field. The electron can experience only electrical field without magnetic field only in the case when both the electron and the electrical field do not move. When electron moves perpendicularly to the electrical field, additionally to the electrical- field component, the electron experiences the magnetic component of the electromagnetic field. This magnetic component is called the magnetic field HSO of spin- orbit interaction.
It is the basic relativistic SO, which describes the fact that an electron is experiences a magnetic field when it moves perpendicularly to an electrical field. This effect can be understood as following. The electrical field is only one specific case of the more general electromagnetic (EM) field. The electron can experience only electrical field without magnetic field only in the case when both the electron and the electrical field do not move. When electron moves perpendicularly to the electrical field, additionally to the electrical- field component, the electron experiences the magnetic component of the electromagnetic field. This magnetic component is called the magnetic field HSO of spin- orbit interaction.
(breaking of time inverse symmetry for weak (or basic) SO) The direction of magnetic field HSO is fixed relatively to the direction of the electrical field and the direction of electron movement. In the case of the forward movement and the direction of the electrical field to the right hand, the direction of HSO is up (See page top fig.). When the movement direction of electron is reversed (or the time direction is reversed), the electrical field becomes toward the left hand and therefore the direction of HSO becomes down. To summarize the origin of the weak SO contains the breaking of time- symmetry
(moderate SO & breaking of time- inverse symmetry)  The example of the moderate SO is the Inverse Spin Hall effect (ISHE) (See my page on the Spin Hall effect). The ISHE describes the fact that an electrical current is created perpendicularly to the flow of the spin- polarized current (spin current) due to spin- dependent scatterings (and SO). E.g. it occurs when the probability of electron scattered to the left and right direction are slightly different with respect to the electron movement direction. This asymmetry of scattering can occurs in a spin- polarized electron gas (e.g. in a ferromagnetic metal) and its origin is the SO.
The example of the moderate SO is the Inverse Spin Hall effect (ISHE) (See my page on the Spin Hall effect). The ISHE describes the fact that an electrical current is created perpendicularly to the flow of the spin- polarized current (spin current) due to spin- dependent scatterings (and SO). E.g. it occurs when the probability of electron scattered to the left and right direction are slightly different with respect to the electron movement direction. This asymmetry of scattering can occurs in a spin- polarized electron gas (e.g. in a ferromagnetic metal) and its origin is the SO.
The reason why the breaking of the time- inverse symmetry is critically important for this effect can be understood as follows. Let us start from the case when there is no current and the time- inverse symmetry is not broken. From a view of a static observer, if for a forward- moving electron the scattered probability to the left is higher than to the right, for a backward- moving electron the probability is higher to the right than to the left. When there is no electrical current and the time- inverse symmetry is not broken, there are equal amounts of electrons moving in the forward and backward directions. In total, the number of electrons scattered into the left and into the right are equal and there is no electron current from the left to right. When there is an electron current in the forward direction and the time- inverse symmetry is broken, the number of electrons moving in the forward direction is larger than in the backward direction. As a result, there are more electrons are scattered to the left than to the right, which results an electron current from the left to the right. To summarize, the breaking the time- inverse symmetry by electrical current creates a perpendicular electron current.
A.(breaking of time- inverse symmetry ) ![]() Magnetic field, spin, electrical current, orbital moment, they are all objects for which the time inverse- symmetry is already broken. They all reverse their own direction when the time is reversed. Additionally, when the time- asymmetrical object is interacting with a time- symmetrical object, the time- symmetrical object may become time- asymmetrical. For example, an external magnetic field may induce a magnetic moment for electron orbital, which initially has no magnetic moment. It is the origin of the PMA effect (strong SO).
Magnetic field, spin, electrical current, orbital moment, they are all objects for which the time inverse- symmetry is already broken. They all reverse their own direction when the time is reversed. Additionally, when the time- asymmetrical object is interacting with a time- symmetrical object, the time- symmetrical object may become time- asymmetrical. For example, an external magnetic field may induce a magnetic moment for electron orbital, which initially has no magnetic moment. It is the origin of the PMA effect (strong SO).
(conservation of time- inverse symmetry )  Some objects can spontaneously break the time- inverse symmetry. For example, assembly of spins + exchange interaction can do it. The spins can spontaneously be aligned along one direction. However, it is a very exceptional case. The time-inverse symmetry is a well- conserved quantity and cannot be broken.
Some objects can spontaneously break the time- inverse symmetry. For example, assembly of spins + exchange interaction can do it. The spins can spontaneously be aligned along one direction. However, it is a very exceptional case. The time-inverse symmetry is a well- conserved quantity and cannot be broken.
(HSO & time- inverse symmetry)  Now I am approaching to the answer to your question. It is very important that the spin- orbit interaction cannot break the time- inverse symmetry by itself. It needs some external breaking (like an external magnetic field or an electrical current) in order to manifest itself. It is a very important feature of SO.
Now I am approaching to the answer to your question. It is very important that the spin- orbit interaction cannot break the time- inverse symmetry by itself. It needs some external breaking (like an external magnetic field or an electrical current) in order to manifest itself. It is a very important feature of SO.
It should be noted that the SO can still influence the electron energy without breaking the time- inverse symmetry. For example, in an atomic gas the SO aligns electron spin along the orbital moment for each individual atom. However, in total for whole atomic gas is not broken due to random orientation of orbital moments in the gas.
In the case of the weak and moderate SO, the electrical current breaks the time- inverse symmetry. In the case of the strong SO (PMA), the magnetic field (magnetization) breaks the time- inverse symmetry.
The Spin-orbit Interaction (SOT) is a general physical effect, which describes a relativistic property of the electromagnetic field. The SOT describes the magnetic field, which an electron experiences, when moving in an electrical field.
The Spin-orbit coupling (SOC) is a perturbation calculation method for the SOT for a specific case when the electric field is the electric field of a nucleus. The SOC assumes that the SOT is small and calculates it as a tiny perturbation. It is an absolutely incorrect assumption. In close proximity of the nucleus the electrical field is huge and the SOT induced by a nucleus is not small at all. For example, in a sample having PMA (See my page on PMA) the SOT magnetic field may be huge (about 10 kGauss).
The SOC perturbation method was developed about 100 years ago, when there were no computers and there was no another option.
The SOC perturbation method often diverges and gives an incorrect result. Therefore, its usage should be minimized.
(about dependency of the spin-orbit interaction of external magnetic field)![]()
![]()
![]()
![]()
Your question is why the spin-orbit interaction depends on an external magnetic field and in which reference it was described for the first time.
This fact is known for a very long time and therefore it is more about the history of Science, in which I am not expert. I am sorry if I refer something incorrectly.
--------------------------------
(SO fact 1) The fact about the relativistic origin of the magnetic field and the existence of the spin-orbit interaction (the existence of the magnetic field of the spin-orbit interaction). This fact is one of basic facts, on which the Special Theory of Relativity was build. Therefore, I think Einstein and Lorentz knew about this fact. Myself, I have read all about this fact (all details and many nice explanations) in Landau textbook "The Classical Theory of Fields"
(SO fact 2) The fact that the strength of spin- orbit interaction (the SO magnetic field) is proportional to the strength of an externally applied magnetic field. This fact are direct consequence of the another important fact about SO:
(SO fact 3) The spin-orbit interaction cannot break the time- inverse symmetry. As a result, in order to manifest itself, the SO needs an external breaking of the time- inverse symmetry (E.g. by an orbital moment or by an external magnetic field or an electrical current etc.).
Fact 2 follows very directly from the fact 3. The strength of SO is zero , when the time inverse- symmetry is not broken (case when the orbital moment is zero, there is no external magnetic field etc.) . The SO magnetic field becomes a non-zero only when the time- inverse symmetry is broken. The strength of the SO ( the strength of the SO magnetic field) becomes larger when the degree of the breaking of the time inverse symmetry becomes larger (e.g. the orbital moment becomes larger or the external magnetic field becomes larger etc.) .
Once again
zero magnetic field -> time-inverse symmetry is not broken -> spin-orbit is zero
external magnetic field becomes larger -> degree of breaking of time-inverse symmetry becomes larger -> spin-orbit becomes larger.
--------------------------------
(fact 3 explanation) Why the spin-orbit interaction cannot break the time- inverse symmetry. This feature is the feature of the time-space symmetry and can be obtained from he Special Theory of Relativity (e.g. see Landau textbook " The Classical Theory of Fields " ). A simplified understanding of the fact 3 can be as follows. The spin-orbit effect is a relativistic effect and therefore can only occur when the object moves or the field, with which the object interacts, moves. The relativistic effect requires a movement. The close movement speed is to the speed of the light, the stronger any relativistic effect is. Any movement means a breaking of the time inverse symmetry. This is why the SO occurs only when the time-inverse symmetry is broken.
------------------------------------
Even though the direct relation between the spin- orbit interaction and the breaking of the time- inverse was understood a long time ago as well as the proportionality of the SO strength to the degree of TIS breaking (e.g., to the strength of the orbital moment or to strength of the external magnetic field), all details and specifics have not been fully understood.
For example, the SO strength depends on the orbital symmetry. Usually the orbital is more symmetric in the bulk of a material and the SO is weaker, but at an interface the orbital becomes less symmetrical and the SO becomes larger.
You can read some details here
This effect is used for molecular-recognition sensor, See here
----------------------------------------------------------------
About experimental measurements.
The dependence of PMA and therefore SO on an external magnetic field is very strong. The experimental measurement of this dependence is rather simple and the measured data well fit to the theory. The anisotropy field is a measurable parameter, which characterizes the strength of PMA and SO.
Near for all nanomagnet, I have studied, I measure the dependence of anisotropy field on a perpendicular magnetic field. Such data contains a lot of important information.
Introductory presentation on this measurement method I gave at MMM 2020 conference. You can watch it here
(about validity of representation of electron orbital as an electron rotating around a nucleus. Electron rotation vs. the orbital spacial distribution vs. breaking time-inverse symmetry)
(Answer). In fact you can and you must. Let me explain by steps
(step 1: about probability) The electron is a wave particle. The probability describes how this wave interacts with external objects. E.g. if you put a point-like electron detector in some point of space, the probability describes efficiency of the detector to detect this electron.
Still as a wave, the electron can move, be reflected and have all properties of a wave.
A good example is a photon, which reflected back and forth between two mirrors. It consists of two opposite moving wave, but the probability does not change in time.
(step 2: about angular momentum): In general, the angular momentum (e.g. L=1) describes the degree of breaking of the time-inverse symmetry. The spin describes the internal breaking of the time-inverse symmetry and the orbital moment describes the spatial breaking of the time-inverse symmetry. Any spatial breaking of the time-inverse symmetry corresponds to some spatial rotation of the object. It is the mathematical fact. Even though the electron orbital might be complex, it can be divided into components, along which the electron rotates into clockwise or/and counterclockwise direction with respect to a fixed axis (axis of the orbital moment). Arbitrary 3D is rather complex (See animation above), but still when electron has a non-zero orbital moment, the rotation in one direction slightly larger than in the opposite direction. It is strictly determined by the degree of the breaking of the time-inverse symmetry.
(step 3: about a complex orbital): The shape of the orbital is not directly related to the breaking of the time- inverse symmetry. These are two different properties, even though they often influence each other and might to be fixed to each other by some specific interaction.
In a hydrogen atom, the orbital of a larger orbital moment have a more complex orbital, but it is not always the case. For example, in a crystal, the orbital moment of localized electrons is usually quenched. It means it is zero, even though the shape of the orbital could be very complex.
(step 4: rotation and symmetry):
Any 1D wave function can be represented as a wave moving forward, a wave moving backward or a standing wave as a sum of waves moving forward and backward.
Any 2D wave function can be represented as waves moving forward or backward or a standing wave. Additionally to that, the wavefunction can be represented as a wave rotating clockwise or a wave rotating counterclockwise or a standing wave as a sum of waves rotating rotating clockwise and counterclockwise.
Any 3D wavefunction is the same as the 2D wavefunction but the rotation is the 2D.
What I want to say that the spacial distribution and the breaking of the time- inverse symmetry are two separate properties of the wavefunction. It does not matter what is the spacial distribution of the wavefunction, the time- inversion symmetry can be either broken or not. Even though sometimes the combination of the other eigen wavefunctions is required to make a specific time- inversion symmetry breaking (e.g. for p- or d- symmetries)
(about rotation speed of electron around atom)
(Answer). It is fast enough. For example, the ratio of the velocity to the speed of light c is equal to the fine-structure constant α (α =1/137) for the first orbit of the hydrogen atom.
velectron=α · c=c/137 (q1)
c is speed of light.
In fact, Eq.(q1) is one of definitions of the fine-structure constant α (See here).
(about rotation of an electron around a nucleus)
![]() (from Ekta Yadav) "A conduction electron rotates around each nucleus. " Can you give me some reference for this statement?
(from Ekta Yadav) "A conduction electron rotates around each nucleus. " Can you give me some reference for this statement?
yes, the electron does rotate around a nucleus. Literally. It is not a rotation when one dot is rotating around another dot. For example, as the Earth is rotating (orbiting) around the Sun. The rotation of an electron around a nucleus is more complex, because the electron is a wave. Nevertheless, it is as a real rotation as any rotation could possibly be.
(Rotation in Quantum mechanics. Rotation & electron orbital) In order to understand it, it is better to start from a 1D structure. Let us look at a wave, which is reflected back and forward between two mirrors. This quantum state is static. It does not move in space.. The field distribution is static as well. However, there are waves, which move forward and backward. Next,Let us look at a similar 2D structure. A wave can move around a circle. In this case, the quantum state has a positive and negative orbital moment for a clockwise and counterclockwise rotation, respectively. Additionally, a quantum state may have zero orbital moment. In this case, the state consists of two waves moving or rotating in the opposite directions. This 2d case is similar to the 1D case of a wave reflecting between mirrors. In the 3D case, the electron rotation can be along any 3D vector (x,y,z). Correspondingly, the direction of the orbital moment can be along any 3D vector (x,y,z).
(Rotation & Orbital symmetry) The fact of rotation of the electron around the nucleus has an even more fundamental origin. In nature, all conserved parameters of an object have corresponding broken symmetries. The spin describes the broken time-inverse symmetry. The rotation (as well as the orbital moment) describes more complex breaking of the symmetry. The rotation means breaking of the space symmetry along with breaking of the time- inverse symmetry. The electron of an atom orbital breaks just this specific symmetry corresponding to the rotation. Meaning that, judging from the most fundamental definition of the rotation, the electron of an atomic orbital is truly rotating around the nucleus.
(Rotation & Bonding between neighbor atoms) The electron rotation or, the same, the electron having a non-zero orbital moment also means that the spatial distribution of the electron wavefunction is changing in time. When an electron state participates in a bonding between atoms, the spatial distribution of the electron wavefunction is fixed, cannot change in time and, therefore, cannot be rotated. For this reason, the electron moment is quenched meaning the orbital moment is zero and there is no electron rotation around the nucleus (See here).
(larger spin- orbit interaction?: larger atomic number? or a larger degree of breaking the T-symmetry?)
Regarding your question about the increase in spin-orbit interaction (SO) strength with an increase in atomic number: Yes, there is such a dependency, but it is not straightforward. Spin-orbit interaction arises from the relativistic magnetic field generated by an electron’s motion in the electric field of the nucleus. As the atomic number increases, the nuclear charge and its electric field grow stronger, leading to an increase in the SO interaction, which is linearly proportional to the strength of the nuclear electric field.
However, there are several complexities to this trend. First, the nuclear electric field is partially shielded by the electric field of inner electrons, and this shielding effect becomes more significant as the atomic number increases. Second, the strength of SO is influenced more profoundly by the degree of time-reversal symmetry breaking and the specifics of the electron orbitals than by the nuclear electric field alone. For example, the SO strength for conduction electrons in GaAs (with elements of relatively low atomic numbers) exceeds that in uranium (with a much higher atomic number) due to the orbital and symmetry characteristics of the material.
(Cold fusion & Spin-orbit interaction )
I am not an expert in LENR, so please keep in mind that my perspective might not be entirely accurate. As I understand it, the key mechanism for LENR is the capture of an orbital electron by the nucleus, resulting in the formation of a neutron via the interaction between a proton and the captured electron.

 Importance of the electron size
Importance of the electron size ![]()
 (Key factor for cold fusion): Reduction of the size of orbital electrons to be comparable to the size of nucleus.
(Key factor for cold fusion): Reduction of the size of orbital electrons to be comparable to the size of nucleus.
![]() (fact):
(fact):
 A positively charged positron annihilates almost instantly with a negatively charged electron because they have nearly identical sizes. In contrast, in an atom, a negatively charged electron does not annihilate with a positively charged proton to form a neutron, primarily due to the vast difference in size between the electron's orbital and the nucleus —the electron orbits the nucleus at distances thousands of times larger than the size of the proton (~size of nucleus). Only under extreme conditions, such as the immense gravitational pressure inside a massive star collapsing into a neutron star, the electron and the proton combine together into a neutron. This process occurs in neutron stars, where the star's enormous gravitational force reduces the size of electron orbital allowing all protons and electrons to merge, forming a dense mass of neutrons.
A positively charged positron annihilates almost instantly with a negatively charged electron because they have nearly identical sizes. In contrast, in an atom, a negatively charged electron does not annihilate with a positively charged proton to form a neutron, primarily due to the vast difference in size between the electron's orbital and the nucleus —the electron orbits the nucleus at distances thousands of times larger than the size of the proton (~size of nucleus). Only under extreme conditions, such as the immense gravitational pressure inside a massive star collapsing into a neutron star, the electron and the proton combine together into a neutron. This process occurs in neutron stars, where the star's enormous gravitational force reduces the size of electron orbital allowing all protons and electrons to merge, forming a dense mass of neutrons.
In an atom, the orbital electron and the nucleus proton do not normally interact due to their vastly different sizes. Any quantum-mechanical interaction depends on the overlap integral between the wavefunctions of the interacting particles. Simply put, interaction is significant only when the particles have comparable spatial sizes.
The nucleus is extremely small because it is a composite particle, its size determined by the strong nuclear force. In contrast, the electron, being an elementary particle, forms much larger orbitals, with their size defined by the relatively weaker Coulomb interaction with the nucleus. The electron’s orbital size cannot shrink below a certain limit set by Heisenberg’s uncertainty principle (the strength of the Coulomb interaction between the electron and the nucleus).
Due to this vast size difference, electrons form atomic structures around the nucleus instead of collapsing into it. This contrasts sharply with electron–positron interactions, where both particles have similar sizes and thus immediately collapse into each other, annihilating in the process.
For LENR to occur, the electron’s orbital must be compressed to a size comparable to the nucleus. This is analogous to neutron star formation, where outside pressure forces orbital electrons into the size close to the size of the nucleus. As the electron and proton sizes become comparable, the electron and proton combine into a neutron.
![]() Is the spin- orbit interaction strong enough?
Is the spin- orbit interaction strong enough?
In LENR, I believe that the key is not the shifting of orbitals but rather the squeezing of electron orbitals to sizes comparable to that of the nucleus. For this squeezing to occur, extremely strong forces are needed. Among known forces, the Coulomb interaction within solids is probably the strongest available in a solid.
Although the spin–orbit interaction is strong compared to many other interactions, it is still 2–3 orders of magnitude weaker than the exchange interaction (spin–spin coupling). It is important to note that the exchange interaction is fundamentally a quantum mechanical effect — effectively a spin-dependent modification of the Coulomb interaction. In simple terms: the exchange interaction is just a spin-dependent form of the Coulomb interaction, and its strength is comparable to or slightly less than that of direct Coulomb forces. neutron.
![]() Is there any influence of direct magnetic dipole-dipole?
Is there any influence of direct magnetic dipole-dipole?
Meanwhile, direct magnetic dipole-dipole interaction is even weaker than the spin–orbit coupling. Because of its weakness, I do not think the direct magnetic dipole-dipole interaction is important for LENR.
![]() Key factor for cold fusion: efficient Squeezing of size of inner electrons by external repulsion
Key factor for cold fusion: efficient Squeezing of size of inner electrons by external repulsion
Thus, I think the most effective mechanism for the effective LENR would be the internal pressure exerted by outer orbital electrons through repulsive Coulomb forces for squeezing most- inner electron orbitals, which should lead to the capture of the most- inner electron by the nucleus. This suggests that heavier elements (such as uranium, or possibly cobalt) might be more effective for LENR, as they have more tightly packed inner electrons. Perhaps some complex mechanisms could be designed to further compress the inner electrons by utilizing spin–orbit or exchange interactions. However, this would not be straightforward: inner orbitals are usually fully filled, and their spins are paired and inactive. To activate spin-dependent interactions, one would need to disturb or displace an electron from an inner shell — a challenging task.
--------------------
![]() Cold fusion: Spin-orbit interaction or exchange interaction?
Cold fusion: Spin-orbit interaction or exchange interaction?
I agree with you that both spin–orbit interaction and exchange interaction influence the orbital distribution in a dipolar molecule.
(spin-orbit interaction): The spin-orbit interaction describes a magnetic field of relativistic origin generated by the electric field of the nucleus. Since electrons in a molecule belong to different atoms, they experience spin-orbit coupling from their respective nuclei. Importantly, the strength of this interaction depends strongly on orbital symmetry—the more asymmetric or distorted the orbital is, or the more its center is displaced from the nucleus, the stronger the spin-orbit interaction becomes. This implies that the presence of a nearby atom can modify the strength of the spin-orbit interaction. Although spin–orbit interaction directly influences only the electron spin (not the orbital shape itself), the alignment of the spins can affect the exchange interaction, which in turn can alter the orbital distribution. So even if indirectly, spin–orbit effects can contribute to changes in orbital configurations through their impact on spin alignment and exchange coupling.
(exchange interaction) The exchange interaction modulates the Coulomb repulsion between two electrons depending on their relative spin alignment. This is a strong quantum mechanical effect that significantly alters the orbital distribution in a molecule.
(Averaging out directional features of dipolar molecules in an atomic gas): It should be noted that any directional features of dipolar molecules in an atomic gas may be averaged out due to frequent molecular collisions. For instance, the spin of an individual molecule may be aligned along a specific direction, leading to unique, direction-dependent properties for that particular molecule. However, in a gas, where molecules are randomly oriented and constantly scattering, the spins of different molecules tend to be distributed uniformly in all directions. As a result, these directional features become averaged out across the ensemble, and the spin-dependent properties may not be observable at the macroscopic level.
Although both spin–orbit interaction and exchange interaction undoubtedly influence the orbital distribution in a dipolar molecule, the extent of their impact depends strongly on the specific molecular structure and environment. In many cases, their effects may not be intuitive, and the resulting behavior can be quite complex. Therefore, a clear understanding of the fundamental physics behind each interaction is essential for accurate analysis and interpretation.
--------------------
![]() (comments from David) Now to reply to your comments you wrote: Since electrons in a molecule belong to different atoms, they experience spin-orbit coupling from their respective nuclei. Importantly, the strength of this interaction depends strongly on orbital symmetry So the coupling should be higher about hydrogne or lithium in the case i described ? It should be noted that any directional features of dipolar molecules in an molecular gas may be averaged out due to frequent molecular collisions. Especially as i saud if we talk about liquid molecules together with nickel particles drowned in it. But the magnetic peaks will realign them temporally. In some other experiment LIH can be used as a plasma and this is this way which will deform more the shape.. by some special signals.
(comments from David) Now to reply to your comments you wrote: Since electrons in a molecule belong to different atoms, they experience spin-orbit coupling from their respective nuclei. Importantly, the strength of this interaction depends strongly on orbital symmetry So the coupling should be higher about hydrogne or lithium in the case i described ? It should be noted that any directional features of dipolar molecules in an molecular gas may be averaged out due to frequent molecular collisions. Especially as i saud if we talk about liquid molecules together with nickel particles drowned in it. But the magnetic peaks will realign them temporally. In some other experiment LIH can be used as a plasma and this is this way which will deform more the shape.. by some special signals.
 Video of Conference presentations.
Video of Conference presentations.
67th Annual Conference on Magnetism and Magnetic Materials (MMM 2022) |
Intermag 2023. Sendai, Japan | |
|---|---|---|
 |
||
| click on image to see YouTube Video | click on image to see YouTube Video | |
| (title): Measurement of strength of spin-orbit interaction | (title): Systematic study of the strength of VCMA effect in nanomagnets of small and large strength of spin-orbit interaction. |
Explanation Video
(video): |
|||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||||||||||||||
| click on image to play it |
![]() Content of this page represents my personal view and it is reflected my own finding. It may slightly different from the "classical" view on the spin-orbit interaction, which is described in following references
Content of this page represents my personal view and it is reflected my own finding. It may slightly different from the "classical" view on the spin-orbit interaction, which is described in following references
I will try to answer your questions as soon as possible