Dr. Vadym Zayets

The spin and charge distributions in samples of different geometries can be calculated from the spin and charge transport equations. It is a set of two differential equations with two variables the chemical potential and the spin polarization sp. The first transport equation describes the charge conservation law. The second transport describes the spin conservation law.

Note: On this page only the case is calculated, when spin direction of all spin polarized electrons is the same over whole sample . When it is not the case, the spin-torque current should be included into calculations. It is done here.

 

---

The same content can be found in this paper (V.Zayets JMMM 2018 ) .

---

Possible confusion!!: from 2014 to 2017 I have used names TIA and TIS for groups of spin-polarized and spin-unpolarized electrons, respectively. The reasons are explained here.

---

---

Spin/Charge Transport Equations

The general equations for change and spin electron transport in a solid, which have two independent variables chemical potential and spin polarization of electron gas sp, are given as

 

.

where

is the conventional conductivity of the metal or charge conductivity; It describes a charge current flow along a gradient of the chemical potential (the Ohm's law).

is the spin-diffusion conductivity; It describes the conventional spin diffusion along a gradient of the spin polarization. In metals the spin-diffusion conductivity is larger than the charge conduct

is the detection conductivity, which describes the fact that a charge may accumulate along a spin diffusion. This electrical charge can be measured and the magnitude of a spin current can be evaluated. Usually is small in the bulk of a semiconductor and a metal (See here. It become substantial in the vicinity of an interface (See here).

is the injection conductivity, which describes the ability of a drift current to transport a spin accumulation; The injection conductivity defines a ratio of how much the spin polarization of the drift current smaller than the spin polarization of the electron gas. It is small in a metal and it is large in a semiconductor.

is an equilibrium spin accumulation in a metal, when there is no current flow. It equals to zero for non-magnetic metals and semiconductors and it is not zero for ferromagnetic metals.

is the spin life time;

is the number of spin states per a volume in metal (It is calculated from the spin statistic. See here);

q is the electron charge.

To note: ,,,,,may depend on spin and charge accumulations.

To note: the value of both the charge conductivity and the spin-diffusion conductivity are positive . It is because of facts that negatively charged electrons flows from a "-" source towards a "+" drain and the a spin accumulation monolithic ally decays from regions of smaller spin accumulation to the regions of higher spin accumulation. The detection conductivity and the injection conductivity can be either positive or negative.

 

 

 

 

 

 

 

 

 

 

 

---

---

 

Derivation of the transport Equations

To note: The spin/charge transport equations are derived from the Continuity equations for the charge and spin

The conservation of charge and spin are fundamental conservation laws of physics. Any possible description of the spin transport should satisfy these conservation laws.

---

 

We begin with finding the number of electrons in the group of spin-polarized and spin-unpolarized electrons and clarifying how these numbers are influenced by spin relaxation and spin pumping

Number of electrons in groups of spin-polarized and spin-unpolarized electrons. Spin relaxation & Spin Pumping.

Number of electrons in groups of spin-polarized and spin-unpolarized electrons

The half-filled states are major carriers of the spin and the charge in an electron gas. Note: "full" states also transport the charge.

The number of the spin states can be calculated from spin statistics as

where is the total number of the half-filled states in both assemblies, sp is the spin polarization of the metal..

may depend on both the spin and charge accumulations.

only slightly depends on the spin polarization sp. For example, in the case of metals with a constant density of the states at the Fermi energy (See here) :

where D is the density of the states near the Fermi energy.

It should be noticed that only slightly depends on the spin polarization sp. It decreases about 20 % as the spin polarization increases from 0 to 100%. In contrast, may significantly depend on a charge accumulation. For example, in the case of a non-degenerate n-semiconductor increases exponentially with linear increase of the Fermi energy. In a metal it could be assumed that only weakly depends on the charge accumulation.

 

Spin Relaxation & Spin Pumping.

Due to spin relaxation the electrons are converted from the TIA assembly to the TIS assembly. Due to the spin pumping the conversion is in the opposite direction (for example, see here). The number of the spin states in each assembly changes as

where is the spin relaxation time and is the spin pumping effective time.

Substituting Eqs. (3.1) into Eq. (3.3) gives

In an equilibrium the number of the spin states in assemblies does not change. Therefore, the spin polarization sp0 of equilibrium can be calculated from condition

From Eq. (3.5) the spin pumping effective time can be found as

Substituting Eq(3.6) into Eq. (3.4) , the rate of electron conversion between assemblies due to the spin relaxation & pumping is given as

---

Spin & Charge Currents

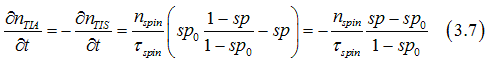
In metals and semiconductors the spin and charge currents flow along the gradients of the chemical potential and the spin polarization sp.

To note: in contrast to the classical model of the electron gas, where there is two independent chemical potentials for spin-up and spin-down electrons, in the presented model there is one chemical potential for both assemblies. It is because the electrons of the TIA and TIS assemblies (spin-polarized and spin-unpolarized electrons) always have the same Fermi energy.

The current of electrons of the TIA and TIS assemblies can be expressed as

where conductivities can be calculated by solving the Boltzmann transport equations.

To note: kT in Eqs (3.8) is introduced just for convenience. This makes all conductivities to be of the same unit

To note: Classical definition of the direction of an electrical current is along movement of a positive particle and opposite to the movement of electrons.

The electrons of the TIA assembly are spin-polarized. When they defuse they transport spin and charge. In contrast, the electrons of the TIS assembly are not spin-polarized and they only transport the charge. Therefore, the spin and charge currents can be calculated as

where the charge, spin-diffusion, detection and injection conductivities are defined as

Note: the multiplier sp is introduced in the front of and based on the requirement of the same time-inverse symmetry of both sides of Eqs. (3.10).

 

The Spin/Charge Transport Equations

The transport equations can be derived from the continuity equations for the spin and for the charge. The continuity equations describe the conservation laws for the spin and the charge, which require that the amount of the spin and the charge at each special point may change only when electrons are converted between assemblies or when electrons defuse to the point from a surrounding.

Wikipedia about continuity equations

The continuity equations for the charge reads:

where n is the number of electrons. In a static case .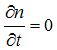

Since only electrons of the TIA assembly are spin-polarized, the continuity equations for the spin reads:

Substituting Eq. (3.7) into Eq.(3.11b), we obtain

 

Substituting Eqs.(3.9) into Eqs (3.12) gives

 

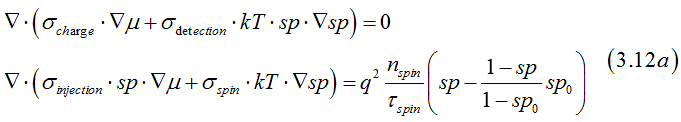
The Spin/Charge Transport Equations are obtained as

 

 

---

---

 

Spin diffusion length in a non-magnetic metal

In a simplest case of a spin diffusion in a bulk of non-magnetic metal, in which

the Spin/Charge Transport equations are simplify to

In the case when does not depend on sp, Eq. (4.1) can be simplified to the Helmholtz equation

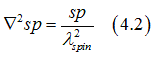
where spin diffusion length is calculated from Eq. (4.1) as

In the case of a metal (See here)

where D_F is the density of states at the Fermi energy

Substituting Eq. (4.4) into Eq. (4.3) gives

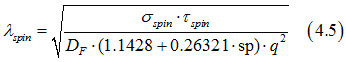
In the case of an isotropic metal with a low density of defects, the conductivities can be calculated as (See here)

where tau_k is the momentum relaxation time, v_F is the electron speed at the Fermi sphere. The value of A(sp) is between 1.1 and 1.5

Substituting Eq. (4.6) into Eq. (4.5) gives

or

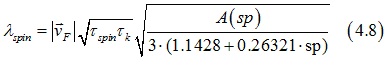
In case of a non-magnetic metal the mean-free path can be calculated as (see here)

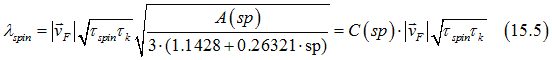
To note: The mean-free path depends on the electron energy (See here). The mean-free path of Eq. (15.5) is the effective mean free path in metal.

---

---

Spin Diffusion length in ferromagnetic metals

Spin diffusion length shortens as the equilibrium spin polarization sp0 of the ferromagnetic metal increases !!!

 

The spin diffusion length in a ferromagnetic metal is calculated as

where sp0 is the equilibrium spin polarization of the ferromagnetic metal and

 

---

 

Another form of the spin/charge transport equation

Sometime this form is more convenient

 

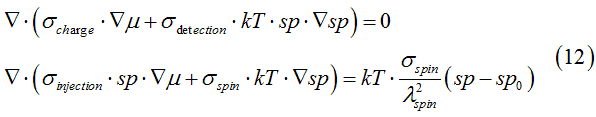
where the spin diffusion length is calculated as

 

It should be noted that Eq. (11.2) is obtained ignoring the dependence of the number of the spin states n_spin on the spin polarization of the electron gas (See here). However, the variation of n_spin is only 10 % (See here) and Eq. (20.1) can be considered as a good approximation

---

 

---

Comparison with transport equations obtained by older models. The limitations of the older models.

(Model 1) Oldest and simplest spin transport equation is described by the Helmholtz equitation (T. Valet and A. Fert, Phys. Rev.B. 48, 7099 (1993) )

This transport equation simplifies the spin transport only to a simple diffusion of particles.

Transport equation for model 1 is:

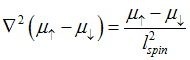
where are chemical potentials for spin-up and spin-down electrons and is the spin diffusion length

 

Incorrect assumptions of this model:

1. Ignoring the important fact, that spin diffusion may accompanied by charge diffusion.

2. Ignoring the energy distribution of spin-polarized electrons. The model assumes that all spin polarized electrons have the same spin transport properties..

3. Incorrectly assuming that spin-up and spin-down electrons may have different Fermi energy and different chemical potentials. It is incorrect assumption because frequent spin-independent scatterings mix up electrons of all spin directions and ensure that electrons of spin-directions have the same Fermi energy and the same chemical potential..

4. Incorrectly assuming that transport of spin-up and spin-down is independent. This is only possible only when the time-inverse symmetry is broken even for group of the spin-unpolarized electrons (See below). This is the incorrect assumption of this model.

This transport equation simplifies the spin transport only to a simple diffusion of particles. Such description ignores several important facts. It is assumed that the spin current diffuses without any accompanied diffusion of the charge. This assumption means that in the case of the spin diffusion it is always an equal amount of spin-polarized and spin-unpolarized electrons move in opposite directions. As it is shown above, this assumption may be only valid in case of transport in bulk of a metal. However, in general case this assumption is not correct and the spin diffusion may be accompanied by charge diffusion. For example, such charge accumulation along the spin diffusion is the origin of the effect of the spin detection. Another over-simplified assumption of this model is the assumption that all conduction electrons have the same spin-transport properties. It is not correct. The spin-transport properties of electrons of energy higher and lower than the Fermi energy are substantially different. For example, in a semiconductor for the same polarity of the applied electrical field the direction the spin drift current is opposite for the holes (electron energy is lower than the Fermi energy) and the electrons (electron energy is higher than the Fermi energy). As it is shown above, in a metal there is a similar dependence of the spin transport properties on electron energy.

In case if the conductivities of spin-up and spin-down electrons would be different, the spin-up and spin-down electrons would have different transport properties and therefore they could be distinguished by their spin-down/spin-up projection along one fixed axis. Spin-unpolarized current is the sum of the spin-up and spin-down currents. That means the time-inverse symmetry is broken even for group of the spin-unpolarized electrons. This is the incorrect assumption of those models. The total spin of the group of spin-polarized electrons is zero. Therefore, the time inverse-symmetry of this group should not be broken, there should be no any distinguished direction for this group and all directions should be absolutely equal. For example, in a ferromagnetic metal the time-inverse symmetry of the group of spin-unpolarized electrons (total spin is zero) is not broken along metal magnetization direction. It is broken only for the group of the spin-polarized electrons (total spin is not zero).

Merit of the model 1

For the first time it describes a possibility of spin diffusion without the transport of the charge.

(Model 2)The model assuming different conductivities of spin-up and spin-down electrons (V.Zayets, Phys. Rev.B. 86, 174415 (2012)) See here.

This model describes the charge accumulation along spin diffusion, the spin detection effect. However, 3 remaining problems of model 3 are not resolved for this model.

Transport equations for model 2 are:

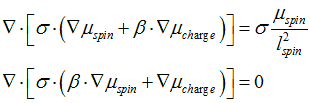
where 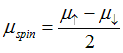is the difference chemical potentials for spin-up and spin-down electrons; is the conventional chemical potential; and is the relative difference in conductivities for spin-up and spin-down electrons.

 

(Correct Model)

Above-described model correctly describes both the charge and spin transport, it does not violate the low of the time-inverse symmetry and it correctly describes the fact that spin-polarized and spin-unpolarized electrons have different energy distributions.

Transport equations of the model, which is described above, are: