Spin. Fundamentals. V.Zayets

For example, the particle energy corresponds to the continuity of the time. The continuity of the time means that the Laws of Physics are the same today and tomorrow. A particle with a non-zero energy, which is always the case, breaks the symmetry of the continuity of the time. Each moment of time is individually different for the particle. For example, when the particle is moving, its spatial position is different at each moment of time and each moment of time is different and not symmetrical for the particle.

The particle momentum corresponds to the continuity of the space, which means that the laws of the Physics are the same here and near the Moon. A particle with a non-zero momentum breaks the symmetry of the continuity of the space. The spatial positions, which are one meter away from the center of the particle and, therefore, the symmetry of the continuity of the space is individually broken for the particle.

. Each moment of time is individually different for the particle. For example, when the particle is moving, its spatial position is different at each moment of time and each moment of time is different and not symmetrical for the particle.

The spin corresponds to the breaking of the time- inverse symmetry. It means that some of particle properties changes if the direction of time flow would be reversed..

(note) The spin magnetic moment and the spin angular momentum are the properties, which are consequence of breaking of the time inverse symmetry. E.g. the breaking of the time-inverse symmetry makes the number of Dirac equation twice as many. There are 4 Dirac equations.

Incorrect view of the spin as an internal rotation of an electron

Q. Is it possible that the origin of the electron spin is the rotation of the electron around itself??

Electron can not rotate around itself (its own axis)

An object should have parts in order to able to rotates around itself. The electron does not have parts!!

Or an object should have a asymmetrical shape in order to able to rotates around itself. The electron does not have a shape!!

The rotation of electron around its own axis

When the electron has parts, the rotation can be seen. When the parts vanish, the rotation can not be distinguished.

The real electron is an elementary particle, which does not has parts. Therefore, electron can not rotate around its own axis.

An electron can rotate around another object like nucleus.

When the electron has asymmetrical shape, the rotation can be seen. When the shape is spherical, the rotation can not be distinguished.

The real electron dos not have a shape. Therefore, electron can not rotate around its own axis.

The electron shape is defined by its environment. It is fixed and it can not be rotated.

A. No. It is not correct assumption.

An electron does does not have parts and it does not have a defined shape. Therefore, it can not rotate around its own axis.

The electron is an elementary particle and it does have any parts. Therefore, the electron can not be rotated around itself

The rotation of an object around itself literally means that the parts of the object rotates relatively each other. In case when the object is monolithic without any parts, it can not be rotated around itself, because there is nothing, which could be rotated.

An electron may rotate around another object. For example, in an atom an electron rotates around a nucleus.

An electron has length, which equals to the electron mean-free path. The length of conduction electrons in a semiconductor could be as long as micrometers. In a metal, the electron length is about of a few nanometers. A localized electron has a size of atom, which is about ~0.1 nm. An electron has a width as well. It is defined by electron wave vector and the mean-free path.

Note:

The spin and charge are two independent features of the electron. For example, when two electrons of opposite spin occupy one quantum state. The state has the charge of -2e, but no spin. The neutron has no charge, but it has the spin.

Incorrect view: The spin of electron is not due to the movement (the rotation) of charge inside the electron.

The spin of electron is not due to the charge of the electron.!!!!! It is due the time-inverse breaking for the electron!!

However, the magnetic moment of electron is because the electron is a charged elementary particle.

All particles in Universe are created by breaking of spatial symmetry of vacuum.(See Fig. 10)

When additionally the time-inverse symmetry of vacuum is broken, an elementary particle has the Spin.

Spin & the time-inverse symmetry

The time-inverse symmetry breaking is the most common and simple breaking of symmetry of the vacuum. Therefore, nearly all particles have the spin

Since the spin describes the breaking of the time-inverse symmetry, there are only two possible spin eigen values for any elementary particle!! For this reason, the spin of an elementary particle is described maximum by two wave functions. Often it is called states of the left-rotation and the state of the right-rotation. In case of an electron, the states are called the spin-up and spin-down states. In the case of a photon, the states correspond to left- and right circular polarized photon.

The time-inverse symmetry symmetry of the vacuum is not broken. Therefore, the spin can interact with the field, which time-symmetry symmetry is broken, and the result of such interaction should be the time-inverse symmetric. The time-inverse symmetry symmetry of the magnetic field is broken. As result, the spin interacts with the magnetic field.

If an elementary particle with the spin is not charged (like the neutrino), does it interact with magnetic field?

The magnetic field represents the time-inverse-breaking part of the electromagnetic interaction. The neutrino, which does not interact electromagnetically, should not interact with the magnetic field. However, the common origin of the weak and the electromagnetic interactions, it could be some a very weak interaction of the neutrino with a magnetic field.

In atom an electron is circulating around a proton. Why a reversed atom, where a proton is circulating around an electron, can not be observed? Is that because of the differences of masses (the proton is heavier)?

It is because the electron is an elementary particle, but the proton is a composite particle, which consists of three quarks. The electron can not have a fix tiny length (size), but a composite particle is more close to a point-like particle. Because the proton is a composite particle, its mass is ~2000 times larger than mass of the electron. The difference of masses has some influence, but it is not major influence. For example, the proton has a diameter about 1 femtometer. It is defined by a longest- possible length of a gluon.

See Wikipedia about point-like particles (There are many parts, with which I do not agree)

Spin as a parameter of degree of breaking of the time inverse -symmetry

The time- inverse symmetry for an object means that no property of the object changes when the direction of the time is reversed. Let me give you some examples, when the time- inverse symmetry is broken. (example 1): An object rotating around some axis. When the time is inverse, the clockwise rotation changes into the counterclockwise rotation. (example 2): An electrical current. When the time is inverse, the electron flow to the left changes to the flow to the right. The direction of a magnetic field, which is induced by the current, reverses its direction. In contrast, the electrical charge, the electrical field, and electron mass are not affected by the time-reversal.

Symmetry is critically important in Physics. Emptiness or "nothing" or vacuum is a state of full symmetry. As a result, the "nothing" can not be distinguished by any means. In contrast, an elementary particle is a bunch of broken symmetries, which is stable in time. As a result, an elementary particle can be distinguished from the "nothing". Additionally, any symmetry corresponds to one conserved parameter. For example, the symmetry of absolute value of time corresponds to a conserved parameter called the energy. The symmetry of absolute value of time means that all Law of Physics is absolutely the same yesterday, today and tomorrow. The existence itself of any elementary particle breaks this symmetry. The particle might exist today, but will not exist tomorrow. As a result, any elementary particle has the conserved parameter called the energy. Similarly, any property of an elementary particle has corresponding symmetry. For example, the electrical charge corresponds to the symmetry of a change of the phase of the wavefunction. It means if the phase of the wavefunction of one separated electron is changed, nothing happens to the electron. The spin is the conserved parameter corresponding to the symmetry of the time reversal. If an elementary particle remains exactly the same, when the time is reversed, the particle has no spin. If some property of a particle changes, when the time is reversed, the particle has a non-zero spin.

General Origin of the Spin:

The rotation between components of the quantum field_____

For example, in the case of a photon, the photon spin is due to the rotation between two components of the photon's electrical field (see below).

The spin of a particle with a rest mass can be understood from Einstein's view of an elementary particle (see below).

The quantum field has a spin, because the rotation between its components is affected by the time reversal. For example, if the rotation between components of the quantum field is in the clockwise direction, the time reversal changes the rotation into the counterclockwise direction.

This fact can be understood on an example of the spin of a photon.

Why Must Something Be Rotating Inside the Electron for It to Have Spin?

Two Puzzling Facts:

(fact 1): The Static Nature of the Electron Wavefunction

Without external influence, the electron wavefunction remains completely static, showing no temporal evolution. It proves that there are no rotation parts inside the electron!

(fact 2): Independence of Electron Spin from Electron Size

As an elementary particle, the electron does not have a fixed size; its effective length depends on its environment. The electron length is called the mean- free path. For example, in metals, the electron’s length is a few nanometers, while in semiconductors, it can be tens to hundreds of nanometers.

Despite this variability, electron spin remains constant, suggesting that spin does not arise from spatial motion within the electron. It proves that there are no rotation parts inside the electron.

Additionally, since the electron has no internal structure or parts, it cannot contain components that move relative to each other.

Two Supporting Reasons for an Internal Rotation:

(reason 1): Broken Time-Reversal Symmetry (T-Symmetry)

Spin describes the breaking of time-reversal symmetry (T-symmetry) in the electron. For an electron’s properties to differ in opposite directions of time flow, some internal property must evolve over time.

This suggests that something inside the electron must be dynamically changing, as required by the broken T-symmetry.

What is moving inside the electron allowing its T- symmetry to be broken?

(reason 2): Existence of a Magnetic Dipole Moment

An elementary particle with electric charge and broken time-reversal symmetry (T-symmetry) (therefore possessing the spin) inherently has a magnetic moment, which in turn generates a magnetic field.

Since a static electric charge does not produce a magnetic field, the existence of a magnetic moment suggests that some form of charge motion must be occurring inside the electron. However, this presents a paradox: The electron, as an elementary particle, has no internal structure or constituent parts that could physically move relative to each other. If the charge were physically rotating inside the electron, it would imply an internal structure, contradicting the fundamental nature of the electron as an indivisible particle.

What is moving inside the electron allowing its electrical charge to generate the electrical field?

One possible resolution to this paradox: The polarization of the electron’s quantum field is continuously rotating.

.(As a result:) The internal rotation of the quantum field in a specific direction inherently breaks T-symmetry. This occurs because reversing time would cause the rotation in the opposite direction.

(As a result:) The internal rotation of the quantum field generates the magnetic field, as described by the electron magnetic moment, without requiring classical charge motion

Quantization of Spin

Spin represents the broken time-reversal symmetry (T-symmetry) of an electron. In nature, time can flow in only two possible directions: forward (as it does in reality) or in reverse (hypothetically). Because T-symmetry allows only these two discrete choices, the spin of a single elementary particle can take only two possible values (e.g., +ℏ/2 and −ℏ/2 for an electron).

For a system of two elementary particles, each having two possible spin states, the total number of possible spin configurations is 2^2 = 4. Similarly, for n elementary particles, the total spin can take2^n discrete values.

Spin Direction

If spin represents a property of time, and time itself does not have a spatial direction-being entirely independent of spatial coordinates (x, y, z)-then how does spin acquire a specific direction in space?

General Answer:

The answer lies in the existence of multiple elementary time axes (see here), which, unlike absolute time (which is independent of spatial coordinates), are tied to specific spatial directions. For example, consider a photon moving along the x-coordinate: its time is entirely linked to the spatial coordinate x, as described by the equation x=x0+c t. Every moment of its time is intrinsically tied to its spatial position. The Higgs field plays a crucial role by coupling different elementary time axes. The Higgs field forces the quantum field to reflect in various directions, thereby connecting all elementary time axes into a single universal absolute time that remains independent of spatial coordinates.

Spin arises from the breaking of time-reversal symmetry (T-symmetry) along one of these elementary time axes, which is associated with a specific spatial direction. As a result, spin acquires a spatial direction.

Simple Answer:

According to the Einstein model, an elementary particle with rest mass consists of a vector quantum field that is reflected in all directions by the Higgs field (see below).

For a particle to possess spin, its quantum field must have at least two components that can transform into each other over time—a phenomenon known as quantum field polarization rotation. For instance, if the phase difference between the first and second components is +90 degrees, the component is called left-circularly polarized. Conversely, if the phase difference is -90 degrees, the component is right-circularly polarized. In the case of an elementary particle without spin, the amounts of left- and right-circularly polarized components are precisely equal in all directions. As a result, time-reversal symmetry (T- symmetry) is preserved in every direction. However, for an elementary particle with spin, in one specific spatial direction, the amount of one component (e.g., the left-circularly polarized component) becomes greater than the other (e.g., the right-circularly polarized component). This imbalance breaks T-symmetry along a specific spatial direction, which defines the particle’s spin direction.

What type of rotation does electron spin represent?

Spin does not represent a spatial rotation of the particle around a fixed point-like spatial center, such as the Earth's rotation around the Sun or an electron orbiting a nucleus.

Instead, spin represents the intrinsic rotation or transformation between two components of its quantum field, whose direction is reversed with the reversal of the time flow.

Only possible direction of the spin precession

more about this fact here

(Key Fact): Unidirectionality of Spin Precession

Spin precession can occur only in one direction—specifically, clockwise with respect to the external magnetic field. This is a fundamental consequence of the time-space symmetry, which dictates the dynamic how the locally broken time-reversal symmetry (T-symmetry) of an electron, which is described by the electron spin, behaves within a globally broken T-symmetry, as defined by the external magnetic field.

Under no circumstances can the spin precess in the opposite (counterclockwise) direction.

Only possible direction of the spin precession

Only- possible clockwise precession of the spin	Non-existing counterclockwise precession of the spin

When viewed along the direction of the external magnetic field H—in this case, along the z-axis—the spin precession follows a clockwise trajectory.	Under no circumstances can the spin precess in the opposite (counterclockwise) direction. Spin precession can occur only in one direction: clockwise with respect to the external magnetic field.

click on image to enlarge it

Only possible direction of the spin precession

same directions of rotation	opposite directions of rotation
precession pumping	no effect on precession

When the magnetic field of an electromagnetic wave rotates in the same direction as the spin precession, the precession is amplified, and the precession angle increases.	When the magnetic field of an electromagnetic wave rotates in the opposite direction to the spin precession, the rotating magnetic field has no effect on the precession.

The robustness of the one possible rotation direction for spin precession serves as strong evidence for the fundamental nature of the symmetrical origin of spin.

click on image to enlarge it

Spin of a photon

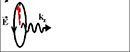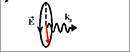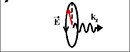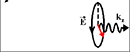
Spin of a Photon

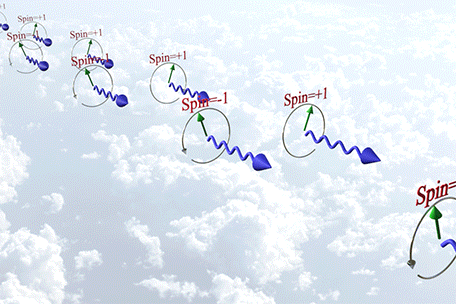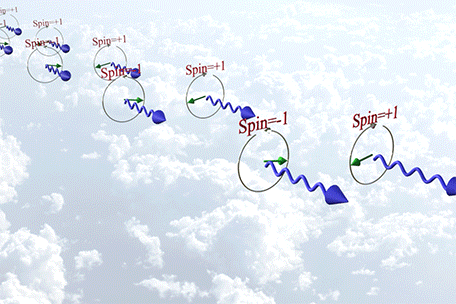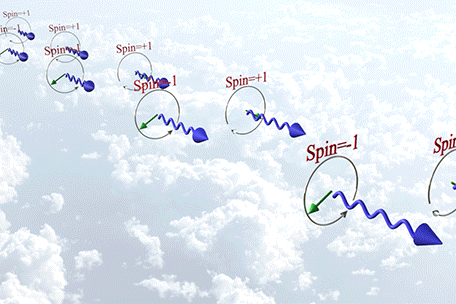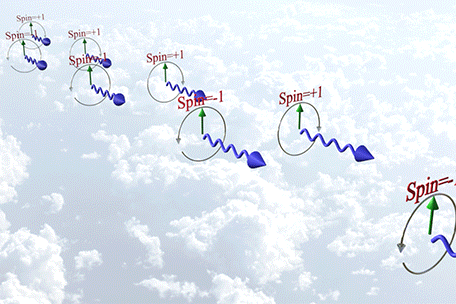There are 3 states of polarization of a photon:

(state 1) Spin=-1; right- circularly polarized light; polarization rotates in clockwise direction;

(state 2) Spin=+1; left- circularly polarized light; polarization rotates in counterclockwise direction;

(state 2) Spin=0;linear- polarized light; (not shown)

green arrow shows the polarization direction

click on image to enlarge it

(fact) A photon may have spin equal +1 or -1, or be without spin.

(why does a photon have a spin?)

A photon has two components of the electrical field, which are directed perpendicular to the photon propagation direction. E.g., if a photon propagates along the z- direction, the photon may have components along the x- and y- directions. There are 3 possibilities for the polarization of a photon. The electrical field or polarization can be fixed along one direction. In this case, the photon has no spin, because the polarization is not changed, when the time is reversed. Another possibility is the electrical field rotates between Ex and Ey components. Such a photon does have a spin, because its polarization is affected by the time reversal. For example, if the rotation of the electrical field is in the clockwise direction, the time reversal changes the rotation into the counterclockwise direction. The clockwise and counterclockwise polarization rotations correspond to the photon spin of +1 and -1.

(substantial difference between the spin of an electron and a photon):

The spin of a photon is always directed along or opposite to the photon propagation direction. In contrast, the spin of an electron can be directed in any direction and is independent of the electron moving direction.

Absence of magnetic moment in a photon

If a photon has the spin, does it have the magnetic moment associated with the spin?

No, the photon does not have a magnetic moment, even though it does have the spin. In order to have a magnetic moment, a particle should have the spin (meaning that the time-inverse symmetry for the particle is broken) and the particle should possess an electrical charge (see below). Since the photon does not carry any electrical charge, it does not have a magnetic moment.

Facts proving the absence of a magnetic moment in a photon:

(fact 1): There is no precession of the spin of a photon in a magnetic field

(fact 2): The energy of a photon is exactly the same in cases when the photon spin is along and opposite to the magnetic field.

Can a single photon be linearly polarized?

A. No, a single photon is always circularly polarized and has spin. Linearly polarized light consists of at least two photons: the first photon is left-circularly polarized, and the second is right-circularly polarized.

(Proof): Single-photon processes dominate in an atomic gas. The atomic gas consists of nearly non-interacting individual atoms. Therefore, the interaction of light with atomic gas is the sum of individual interactions between single atoms and single photons, in which other atoms do not affect each atom/photon interaction. Transitions in atomic gases occur only when the electron reverses its spin and/or orbital momentum. This means that the single photon is always transferring its spin to the electron, implying that a single photon is always circularly polarized and has spin. Since in atomic gases there is no photon-electron interaction in which the photon does not transfer its spin, there is no single photon without spin, and as a result, there are no linearly polarized photons.

In contrast, in solids, groups of photons collectively interact with a collective of interacting electrons, where multi-photon transitions dominate. This means specific single-photon properties do not dominate photon absorption or emission in solids. For example, solid-state lasers always emit linearly polarized light with p- or s-polarization (with TE or TM polarization). This means photons with left- and right-circular polarization are always emitted simultaneously and in phase. External conditions, such as the polarization dependence of mirror reflections, define the laser's output polarization.

It should be noted that, with some limitations, a linearly polarized photon can be considered a single particle. The case of a linearly polarized photon is similar to the case of a quantum state filled by two electrons of opposite spins. Such a quantum state can be considered a single particle with no spin and a charge of -2e. Although this quantum state can be viewed as a single particle, considering it as a sum of two electrons (with some limitations) is easier to understand.

For the same reason, a linearly polarized photon should be considered as a sum of at least two single photons: left- and right-circularly polarized photons.

Einstein's representation of particle with a rest mass

Einstein's representation of a particle with a rest mass

The mirrors represent the Higgs field, from which the quantum field is continuously reflected in opposite direction

click on image to enlarge it

(fact) Einstein considered that any particle with a rest mass (for example, an electron) consists of a massless quantum field, which is moving at speed of light and which is bounced back and forward between two mirrors. The mirrors represent the Higgs field, from which the massless quantum field is reflected.

The energy of this confined state gives the electron rest mass.

This representation of a particle with a rest mass gives a simple and understandable explanation of all effects of the special theory of relativity. For example,

(1) why does the mass of the particle increase with its speed;

(2) why the speed a particle with a rest mass cannot exceed the speed of light.

Einstein's representation of a particle with a rest mass means that

(1) additionally to the fact, that any particle or quantum field cannot move faster than the light speed c

(2) the quantum field cannot move slower than the speed of light

All elementary particles, which have a non-zero rest mass (like an electron), gain their rest mass due to backward and forward reflections in the Gibbs field (like light backward and forward reflections between two parallel mirrors).

Reflection of a quantum field from the Giggs field

(continuous reflection) The reflection is not a point- like, for example, as a reflection of light from a mirror. The quantum field is continuously reflected from the Giggs field as it propagates in it.

Such a reflection is called the distributed- feedback reflection (DFR)

Nowadays, the DBR mirrors are used in the most of commercial semiconductor lasers (See here).

(interaction of a quantum field and the Giggs field ) There is a mutual interaction between any quantum field and the Giggs field. The quantum field is reflected backward by the Giggs field. As a result, the elementary particle gains a rest mass from the Giggs field. The quantum field modulates the Giggs field with its own spatial frequency.

Origin of the Spin of a particle with a rest mass

Spin of particle with a rest mass

A particle with a rest mass is represented as a massless quantum field of the electron, which is bounced back and forward between two mirrors (See above). As the quantum field propagates from one side of the particle to another side, there is a rotation between the two components of the quantum field. The rotation breaks the time- inverse symmetry, which is described by the spin

The spin is conserved after the reflection, for this this reason the spin direction is the same for the quantum field moving to the left and to the right from an observer's view, but the spins are opposite with respect to the move direction of the quantum field.

click on image to enlarge it

(spin & quantum field) A quantum field has two or more components. A rotation between the two components of the quantum field breaks the time- inverse symmetry. The spin of an elementary particle describes this breaking of the time-inverse symmetry.

A particle with a rest mass is represented as a massless quantum field of the electron, which is bounced back and forward between two mirrors (See above). The mirrors represent the Higgs field, from which the quantum field is continuously reflected in backward

(Origin of the spin): a rotation between the two components of the quantum field

In order to have a spin, the quantum field should change (not be equal) when the direction of the time flow is reversed.

For example, if the quantum field rotates in the clockwise direction, the rotation becomes counterclockwise after the time reversal.

It means that the quantum field should have at least two components, which should correspond to the opposite direction of the time flow. For example, the clockwise and counterclockwise rotation of the quantum field.

(note) The quantum field describes a breaking one or several symmetries of our Universe (see here)

(note) Even though the direction of the time flow cannot be literally reversed, the time- inverse symmetry is one of the important symmetries , which determines the particle's existence and which the particle may have or may not have..

Spin conservation during reflection of quantum field from Higgs field

The spin is a conserved quantity. When the quantum field is reflected backward, the direction of the spin remains the same, which means that with respect to the movement direction of the quantum field, the direction of the spin is reversed. For example, if the quantum field rotates in the clockwise direction along its moving direction, after reflection the field rotates in the counterclockwise direction along its moving direction (See the left picture)

(fact) the Einstein's representation of particle with a rest mass gives two possible representation of the spin:

Dirac and Non- Dirac representations of the Spin (see below for details)

Spin & Magnetic Moment

The magnetic moment is a quantity, which describe an interaction of a particle with an external magnetic field

Two vital conditions for a particle to have a magnetic moment:

(vital condition 1): The time-inverse symmetry for a particle should be broken.

(vital condition 2): The particle should possess an electrical charge.

Any charged particle, which time-inverse-symmetry is broken, always has a magnetic moment

(fact): The time-inverse symmetry is broken only for a particle, which has a non-zero spin or/and a non-zero orbital moment

(fact): An uncharged photon has a spin, but does not have a magnetic moment

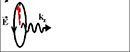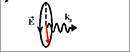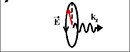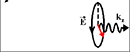
Properties due to existence of a magnetic moment:

(property 1): There is a precession of the spin in a magnetic field

(property 2): The energy of a particle is different when the spin of the particle is along and opposite to the magnetic field.

(note) A photon, which does not possess a magnetic moment, does not have those two properties.

Origin of the magnetic moment and symmetry

Origin of the magnetic moment:

The origin of the electron magnetic moment is nearly the same as the origin of the electron charge. The electron charge is originated from the breaking of the symmetry of the phase of the electron wave function with respect to spatial transformation. Similarly, the electron magnetic moment (spin-related) is originated from the breaking of the symmetry of the phase of the electron wave function with respect to time-reversal.

(gauge symmetry: origin of electrical charge:) The electron wave function has both the phase and magnitude. Only magnitude has a physical meaning which the probability of electron to be at certain spacial point at fixed moment of time (See here for more details). The phase has no physical meaning for a single electron in absence of any neighbor particle. In this case, the changing of the phase does not affect any of the physical parameter of the electron. However, in the electromagnetic field, the phase of the electron wavefunction is locally changed by the electromagnetic the electron energy

(origin of charge) The gauge symmetry becomes locally broken for a spacial transition (e.g. transition along the x-axis)

(origin of spin-related magnetic moment) The gauge symmetry becomes locally broken for a time inverse transformation

Spin vs. Orbital moment. Time- inverse symmetry vs. rotational symmetry.

(fact): The spin and the orbital moment describe breaking of the different symmetries. Even though both the spin and the orbital moment describe a quantum state with a broken time- inverse symmetry, the rotational symmetry, which is described by the orbital moment, has an additional component (the spatial symmetry)

Breaking/ Unbreaking the time inverse symmetry: 2 cases: spin & orbital moment

Unbroken time inverse symmetry. Comparison of 2 cases: (case 1) a quantum state is occupied by two electrons of opposite spins and (case 2) a quantum state is occupied by two electrons of opposite orbital moments

Spin: Breaking time-inverse symmetry only		Orbital moment: Breaking rotational symmetry (= time-inverse symmetry + spatial symmetry )

A quantum state, which is occupied by two electrons of opposite spins, is absolutely equal and undistinguished whether the directions of the spins are up/down or left/right or front/back		Quantum states, which are occupied by two electrons of opposite orbital moments, are different and can be distinguished by the direction of their broken spatial symmetry, even though the time- inverse symmetry is not broken for these states.
Even though you can see a difference in the schematic illustration of these 3 quantum states, they are absolutely identical and undistinguished. All 3 states are described by the same scalar spinor.		The inversion of the direction of the time flow does not affect or change in any way any of these states. It means that the time inversion symmetry is not broken for these states. Since the states are still distinguished from each other, they possess another broken symmetry, which is called the spatial symmetry.
These states are called the spin-inactive states. They play the important role to redistribute the conduction electrons into two groups of the spin- polarized and spin- unpolarized electrons See here).

(absence of magnetic moment & no interaction with external magnetic field): The time- inverse symmetry is not broken for both quantum states, which are shown at the left and the right sides. As a result, both quantum states do not have a magnetic moment and do not interact with an external magnetic field. The broken time- inverse symmetry is essential for a quantum state to have a magnetic moment (See here).

click on image to enlarge it

Visualization of the spin & orbital moment

Spin only	Orbital moment only	Spin + orbital moment

there is a rotation between the two components of the quantum field. The rotation breaks the time- inverse symmetry, which is described by the spin	The wave is circling around an axis, which has a spatial direction and a spatial position. At the back side, the wave is moving from the left to the right. In contrast, at the front side, the wave is moving from the right to the left. This type of the broken time- inversion symmetry is called clockwise rotation. When the flow direction of the time is reversed, the rotation direction becomes opposite, the counterclockwise rotation.	The wave of the quantum field is moving around a circle. At the same time, there is a rotation between the two components of the quantum field. The time- inversion symmetry is broken twice: (1) due to the rotational movement of the wave and (2) due to the rotation between two components of the quantum field. The rotational movement of the wave of the quantum field is described by the orbital moment and the rotation between two components of the quantum field is described by the spin.
(key properties): Time- inversion symmetry is broken. The degree of the broken time- inversion symmetry is the same at any spatial point.	(key properties): Time- inversion symmetry is broken. The degree of the broken time- inversion symmetry is different at any spatial point.	(Dirac representation of the spin): As the wave is moving around the circle, the axis of the rotation between two components of the quantum field remains in the same direction and is independent of the movement direction of the wave.
	The quantum field does not change from a point to a point and has only one component.

Interaction of the spin & orbital moment

(fact) Both the spin and the orbital moment describes the degree of breaking of the time- inverse symmetry. The orbital moment describes breaking of the rotational symmetry, which includes the breaking of the time- inverse symmetry.

(fact) An elementary particle has only one time- inverse symmetry, which could be broken only once. Therefore, in case when a particle has both the orbital moment and the spin, the degree of the breaking of the time- inverse symmetry has both contributions from the the spin and from the orbital moment.

fact) The spin and the orbital moment are not always aligned along each other.

How to distinguish the spin from the orbital moment

(How to do it): If you know the wavefunction of the quantum state you should to following:

(step 1) Inverse the time direction for the wave function

(step 2) Sum-up the original wavefunction and the wave function with reversed time.

Spin & Dirac Equations

Dirac Equation & Spinors

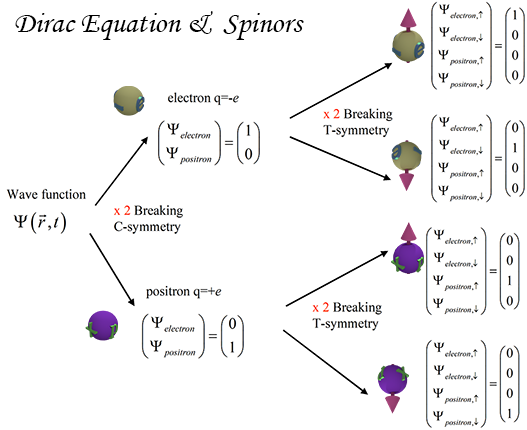Each specific electron of a fixed spin is described by a scalar wave function Ψ(r,t), |Ψ(r,t)|² describes probability to be (to interact with another particle) at point r at a time moment t.

(breaking C-symmetry) : The symmetry, that the charge can be either negative (electron) or positive (positron), doubles the rank of spinor or number of wavefunction, which describes the electron quantum field.

(breaking T- symmetry) : The symmetry, that the spin direction can be either up or down, doubles the rank of spinor or number of wavefunction, which describes the electron quantum field.

In total, the C-symmetry (x 2) and T- symmetry (x 2) makes the rank of 4 for the spinor, which describes the electron quantum field, and, therefore, requires 4 equations (the Dirac Eqs.) to describe this electron quantum field.

click on image to enlarge it

(fact 1)

The Dirac equations describes the quantum mechanical properties of an electron. The solution of the Dirac equation is a 4-rank spinor. The 4-rank spinor is a 4 dimensional vector of 4 wave functions, which transformation properties are following the symmetry of a spinor.

(fact 2): The Dirac tensor for electron quantum field describes all states of the electron. A possibility to have either a negative or positive charge and a possibility to have either spin-up or spin-down spin direction.

( C- symmetry): The symmetry of reversal sign of the charge

The plus and minus charge are fully equivalent. There is nothing, which makes the plus charge better than the minus charge or vice versa. As a result, the spinor of electron quantum field should describe equally the particle of the minus charge (the electron) and the particle of the plus charge (the positron).

( T- symmetry): The time- inverse symmetry, which is described by the spin.

The breaking of the time-inverse symmetry means that for any state (e.g. spin-up state), there is a state (the spin-down state), which is the time- inverse transform from the original state. It means that if the time flow is inverse, the spin-up state becomes spin-down state and the spin-down state becomes the spin-up states. Additionally, the breaking the time-inverse symmetry causes some new properties of particle such as the magnetic moment and the angular moment.

The electron can never be transformed to the positron. Why does the Dirac spinor describe both the positron and electron wave functions?

A1. (general description of all symmetries of quantum field) An actual particle (e.g. an electron) is described by a scalar wavefunction. In contrast, the Dirac spinor describes all possible states of the electron Quantum

A2. (possibility of the annihilation of the electron and positron. Restoring of the C-symmetry) For each the electron and the positron, the C - symmetry is broken. However, the symmetry breaking is opposite. The charge of the electron is negative, but the charge of the positron is positive. When the electron and positron collide to each other, the breaking of the C-symmetry disappears and a result of the colliding is a charge-free photon.

A3. (relativistic decrease of the charge, when the particle speed becomes close to the light speed) An In fact, a moving electron has a small component of the positron wave function. The positron component becomes larger and the charge of the electron becomes smaller, when the electron speed becomes close to the light speed. A particle, which moves at the light speed, cannot have a charge, because the charge is originated from breaking the gauge transformation symmetry (See above) and such symmetry breaking is not possible at the light speed.

The time flows in one direction from the past to the future. There is no time flow from the future to the past. Since time inverse can never occur, why the time- inverse wave function is included into the Dirac spinor?

A1. It only means that a specific symmetry for a particle is broken.

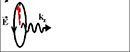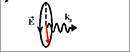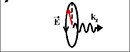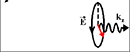
Why is the spin of an electron (S = +/- 1/2) half of the spin of a photon (S = +/- 1)?

What do the numbers 1/2 and 1 specifically represent?

The classical interpretation suggests that the spin of an electron is 1/2 because it is a fermion, while the spin of a photon is 1 because it is a boson. However, there is no physical meaning behind this claim and these numerical values, 1/2 and 1, lack specific physical significance in relation to spin.

(The concept of spin is better described using a boolean value rather than a decimal number.):

Specific numerical values for the spin do not carry particular meanings. The spin is a description of broken time-inverse symmetry. Only a reversal of the spin value has a meaning, which corresponds to the reversal of the broken time inverse symmetry. For a single elementary particle, the absolute value of the spin has no meaning.

Time-inverse symmetry can either be broken or unbroken, and correspondingly, spin values can only be 'yes' or 'no,' representing an event as either true or false. The spin value is related to the fact that the time flow can be either forward and backward directions. Therefore, the spin value can be either plus & minus or true & false.

This binary nature of spin applies universally, whether it is for a photon or an electron. The broken time- inverse symmetry is an universal feature of any quantum field. There is no reason why the spin value should be different for different quantum fields like the electromagnetic field and the electron quantum field. Even more, there is no reason why the spin value should take any specific number for any specific quantum field. The absolute value of the spin has no physical meaning.

(Interaction between a fermion and a boson. The reason for spin values 1/2 and 1):

The interaction between a boson (such as a photon) and a fermion (like an electron) results in the transfer of spin or the transformation of broken time-inverse symmetry from the boson to the electron. For example, if the electron's spin value is initially assigned as -1/2, it becomes +1/2 after the interaction, because the direction of the broken time- inverse symmetry and, therefore, the spin direction are reversed. The difference between initial and final spin values is +1, Therefore, it is natural to assign the spin value of +1 to the photon. However, it's crucial to understand that the same spin value is effectively transferred from the photon to the electron, but not added. If the spin direction of the photon was to the right, the spin of the electron became to the right. It is just an event of the spin directed to the right from the photon to the electron. In essence, a boolean operation better describes spin transfer for a single elementary particle than numerical addition or subtraction. The reason for assignment of spin value -1/2, +1/2 to the electron and +1 is only to use the addition operation for the spin transfer instead of a boolean operation.

Reason why electron spin=1/2, but photon spin=1

Interaction of a fermion with a boson

Electron arrived from upper- right corner		Electron arrived from upper- left corner

Two electron spins directed up-right created from one photon spin.		Two electron spins directed up-left created from one photon spin.

In each case, one photon results in two electrons with spins parallel to the spin of the photon. This is the reason why the spin of a photon is assigned to be twice that of an electron.

Initially, the ground state is occupied by two electrons with opposite spins. Since time-inverse symmetry is not broken in this state, it can be represented as a single elementary particle with a charge of +2e. When a photon interacts with these electrons, it breaks the time-inverse symmetry for the electrons. The photon transfers its spin to the electron, whose spin is opposite to the photon spin, causing the electron's spin to reverse. The electron whose spin aligns with the photon's spin remains unaffected. As a result, one photon spin creates two electron spins.

(undefined spin for the ground state) The ground state is filled by two electrons of opposite spin. The time- inverse symmetry is not broken for the ground state. It means that the two electrons combine into one single particle with no spin and charge -2e. The absorption of photon breaks the time- inverse symmetry for the state creating two opposite spins with the direction along the photon spin. The photon spin transforms to one electron reversing its spin.

click on image to enlarge it

(spin for a fermion and a boson):

Breaking of time- symmetry is absolutely identical for a fermion and a boson. It means that the spin is identical for the fermion and the bosom and can take only the true or false number corresponding to broken or non- broken time- inverse symmetry.

The existence of spin in both the photon and the electron corresponds to the circular rotation of their respective quantum fields.

(spin direction for an elementary particle with a rest mass and massless particle):

For massless particles like photons, spin is strictly directed along or opposite to the particle's propagation direction. In contrast, for elementary particles with rest mass, spin can have any orientation in 3D space. See above chapter named "Einstein's representation of particle with a rest mass".

(total spin of several elementary particles):

When multiple elementary particles have parallel spins, their total spin is summed up. For example, if there are 21 electrons with parallel spins, the spin of each electron is assigned 1/2, the total spin equals 10.5. The value 10.5= 1/2*21 indicates that there are 21 particles with broken time-inverse symmetry in the same direction. When particle spins are not parallel, they are summed based on the properties of time-inverse symmetry.

(Spin and orbital moment):

It's important to note that spin and orbital moment represent two distinct broken symmetries. Spin represents broken time-inverse symmetry, while orbital moment represents the broken rotational symmetry. Therefore, spin and orbital moment are two distinct parameters that cannot be added together and must always be distinguished from each other.

An important fact is that the rotational symmetry includes into itself the time- inverse symmetry (See here). Both the spin and the orbital moment affects the magnetic moment of the elementary particle. An elementary particle exhibits a magnetic moment under two conditions: it possesses an electric charge, and its time-inverse symmetry is broken. Consequently, both orbital moment and spin contribute to the magnetic moment of an electron. This magnetic moment affects the energy splitting of an electron in a magnetic field and is measurable.Due to this property the total moment J of elementary particle is often used in calculation, but it has little physical meaning because the spin and the orbital moment represent different symmetries.

Quantum Mechanic and Magic in Physics

click on image to enlarge it

Physics has no magic

Maybe the desire to create a magic lies deep in the human nature. Anything what humans were not able to explain, is considered to be the magical until a scientist logically explains it and all magic vanishes.

Everything in Quantum Mechanic can be explained with logic and reasons.

All magic in Quantum Mechanic is originated from poor knowledge, tricks and lies.

There is nothing in Quantum Mechanic which could not be explained logically and based on the Laws of the Symmetries and the Conservation Laws of the Physics.

Incorrect explanation of the nature of the Spin

Following incorrect explanation of the results of the Stern–Gerlach experiment (See below), the incorrectly- assumed Quantum nature of the Spin was accepted for a long time. Even though the magical nature of the spin contradicts with several Laws of Physics and Quantum Mechanics

Perpetual motion machine cannot ever exist because of the energy conservation law

The energy conservation law does not allow to built a perpetual motion machine of any design

For hundreds years "engineers" and "scientists" are unsuccessfully challenging the fundamental energy law trying to built the perpetual motion machine.

Similarly, the fundamental spin conservation law are challenged by many scientists, which support the magical spin nature.

(incorrectly- assumed Quantum nature of the Spin)

The direction of the electron spin is not fixed, but depends on the measurement geometry. When the direction is fixed (e.g. the vertical direction), it fixed the possible spin direction and the spin can have either spin-up or spin-down directions along the fixed measurement direction

Contradictions of the Quantum Nature of the spin with several well- known well- verified Laws of Physics and Quantum Mechanics

(contradiction with spin conservation law): The claim, that the spin direction is not fixed, but determined by the measurement geometry, directly contradicts with the well-verified spin conservation law.

Any the conservation law in Physics corresponds to some symmetry of the space- time of our Universe (See below). The spin conservation law corresponds to the time- inverse symmetry of our Universe. This symmetry is a similar to the symmetry of continuos time flow, which means that all Physics laws will be same tomorrow as they are today. Therefore, the violation of the spin-conservation law as incorrect as the violation of the energy conservation law!

(contradiction with Dirac equations): The claim, that the spin direction is not fixed, but determined by the measurement geometry, directly contradicts with the Dirac equations, which only have a physical meaning when both the electron charge and the electron spin are fixed.

The solution of the 4 Dirac equations is a 4-rank spinor. However, a particle (an electron) is described by a scalar wave function. The 2 x functions describe a particle with opposite charge and 2x functions of the opposite spin. In order for spinor to become a scalar wavefunction both the electron charge and the electron spin should be firmly fixed. As a result, any realistic particle (an electron or a positron) has the fixed charge -e or +e and the fixed spin (the fixed spin direction)

(contradiction with fact of a single direction of the time flow): The time flows in one direction in our Universe from the past to the future. The claim, that the spin direction is not fixed, but determined by the measurement geometry, directly means that the flow of time is not fixed.

The spin describes the breaking of time inverse symmetry. The breaking of time-inverse symmetry is described by a 2-rank spinor, which contains two wavefunction. The first wavefunction describes the actual wavefunction of the electron. The second function describes the wave function of electron, which would be if the direction of the time flow were reversed. The claim, that the spin direction is not fixed, but determined by the measurement geometry, directly means that the direction of the time flow is not fixed, but is determined by the measurement geometry. It is clear that it is a nonsense.

(contradiction with experimentally- observed spin-related effects): All known experiments in magnetism are well explained using the Spin Conservation Law and without use of the incorrectly- assumed Quantum Nature of the Spin

Why so many people, including some science, does not accept the fundamental conservation Laws like the energy conservation law and the spin conservation law?

The people need a magic. The straightforward facts and laws of Physics are bored. For the magic people are willing to pay.

Stern–Gerlach experiment. Incorrect interpretation.

Magic, which lived over a hundred years.

Original paper translated in English is here

wiki page about Stern–Gerlach experiment is here

See the incorrect explanation of the results Stern–Gerlach experiment in Dr. Matt O`Dowt video time: 5:10

many details about the Stern–Gerlach experiment are explained in this YouTube Video

Misinterpretation of the Stern–Gerlach experiment is one of longest- lived misinterpretations of an experiment in Physics.

short explanaition about misinterpretation of the Stern–Gerlach experiment is below in question section

(goal of experiment): A measurement of distribution of the spin directions in an atomic gas or an electron gas.

(effect behind the experiment):In a gradient of the magnetic field, a particle with the spin experiences a mechanical force. The direction and the strength of the force depends on the particle' spin direction with respect to the gradient. As a result, a particle with a different spin direction moves in a slightly different direction due to a different mechanical force. A measurement of distribution of the particles passing a gradient of the magnetic field gives the distribution of the spin directions of these particles.

Stern–Gerlach. Original measurement data

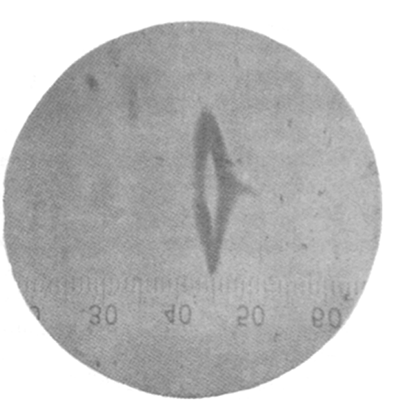Two lines are detected. Each line corresponds to a beam of Ag particles, in which the spins of all particles are aligned in one direction along the magnetic field of the magnet.

See note about the magnet design here or the magnet design in the original paper here.

The image data is Fig.3 of the original paper (See here)

click on image to enlarge it

(incorrect quantum explanation):

(incorrect conclusion 1) Since there are only two detectible lines, the spin may have only two directions, for example, spin-up and spin-down.The spin directions cannot have some 3D distribution, for example, a spherical distribution.

(incorrect conclusion 2) Since the detected lines are rotated when the magnet is rotated, the spin is not a defined property until it is measured. For example, until an event of measurement, the spin can be in either of spin-up/spin-down or spin-left/spin-right or spin-front/spin-back configurations.

(Why is the quantum explanation incorrect?): Similar to the energy, the spin is a strictly conserved parameter. According to the Noether rule, the spin conservation law is due to the time- inversion symmetry. As a conservation parameter, the spin cannot be undefined or be changed depending on a measurement. The spin can be changed only when a particle interacts with another with the spin. It is similar as the energy of a particle cannot be changed unless a particle interacts with another particle. The quantum explanation of the spin behavior in the Stern–Gerlach experiment violates the strict spin conservation law.

(missing effect for the correct and simple explanation): It is very important that the results of the Stern–Gerlach experiment are influenced not by one, but by two effects. The 2nd effect is the alignment of the spin along the direction of the magnetic field.There is a spin precession and a spin precession damping in a magnetic field. As a result of the damping, the spin is aligned along the direction of the magnetic field. The alignment time is usually very short.

(the correct and simple explanation of Stern–Gerlach experiment): A gradient of a magnetic field means that the magnetic field changes from one value to another value. There are only two possibilities for a design of the magnet for this experiment. The 1st possibility, which I guess was used in the Stern–Gerlach experiment, when there is only one gradient. In this case, the magnetic field changes from a minus value to a plus value along the magnet gap. E.g. at the left side of the gap at x=-a H=-H0 and at the right side of the gap at x=+a H=+H0. The gradient equals =H0/a The spins of particles, which enter the gap between x=-a and x=0, are aligned in the minus direction along -H. As a result, the particles are moved to the left along the gradient. The spins of particles, which enter the gap between x=0 and x=+a, are aligned in the plus direction along +H. As a result, the particles are moved to the right along the gradient. As a result, there are two detected lines!!!!

(details of Stern–Gerlach experiment): Electrons of different spin polarization, which are emitted by an electron gun, pass through a spatially varying magnetic field and are detected at a detection screen. In a spatial gradient of a magnetic field, an electron experiences a mechanical force (See below), which pushes the electron to move along the gradient. The direction and the strength of the force depends on the particle' spin direction with respect to the gradient. As soon as the particle enters the magnetic field, its spin is aligned along the magnetic field. At different sides of the spatial point where the magnetic field changes its polarity, the spins of moving particles are opposite. As a result, the particles in two regions of the opposite directions of the magnetic field, moving in the opposite directions resulting in two detected spots.

(result of experiment): The electrons are detected at two lines or spots (the left and the right spot). When the gradient of the magnetic field is rotated 90 deg, the two spots are also rotated 90 deg. Both the gradient of the magnetic field and the regions of opposite polarities of the magnetic field are rotated with a rotation of the magnet. As a result, the detected lines are rotated when the magnet is rotated!!!

Stern–Gerlach experiment

gradient of magnetic field from right to left	gradient of magnetic field from down to up

Fig. 44 (experiment details & result) A beam of electrons of different direction is passes through a gradient of magnetic field. In a gradient of a magnetic field an electron experience a mechanical force (See here) and moves along the gradient in order to minimize its magnetic energy. The force and direction of the electron movement depends on the electron spin direction. The electron final position is detected by the electron detection screen (the screen, which used to be in an old TV set). Two spots are detected, which correspond to the spin up and spin-down directions. When the gradient of the magnetic field is rotated 90 degrees, the positions of two spots are rotated as well.

( puzzle of experimental observation) At electron gun, the spins of electrons are distributed equally in all directions. Since electrons of a different spin direction experience a different force. Therefore, the electrons should be distributed continuously through the screen. Instead only two discreet spots are observed experimentally.

( incorrect explanation) The direction of the electron spin is not fixed, but depends on the measurement geometry. When the direction is fixed (e.g. the vertical direction), it fixed the possible spin direction and the spin can have either spin-up or spin-down directions along the fixed measurement direction. This explaination violates the spin conservation law.

( simple & correct explanation) Additionally to the movement along the gradient of magnetic field, the electron experiences another effect, which is completely ignored by the quntum explanation. The electron spin is aligned along the magnetic field due to the effect of the precession damping (See here). In a gradient of magnetic field, the magnetic changes from a positive value (up-direction) to a negative direction (down- direction). In the middle there is a point when the field is zero. Independently of the initial spin direction, the spin of all electrons, which move from the left side of the zero- field point) are aligned up along the up direction of the magnetic field in this region. As a result, all electrons in this region are forced to move to the left. The spin of all electrons, which move from the right side of the zero- field point) are aligned down along the down- direction of the magnetic field in this region. As a result, all electrons in this region are forced to move to the right. Since the electron spin is aligned along the magnetic field very quickly, the final position of electrons on the detection screen practically does not depends on initial spin it only depends on the electron position with respect to the zero- field point. naturally, there are two detection spots. When the gradient is rotated, the position of the detection spots are rotated as well. Therefore, the results of Stern–Gerlach experiment are 100 % fit to known Laws of Physics and Quantum Mechanics without any magic.

click on image to enlarge it

(Why was the measured result considered a problem for a long time? ): Why was the measured result considered a problem for a long time? ): At the muzzle of the electron gun, the electrons are not spin- polarized and, therefore, their spins should be distributed equally in all directions. Since the spin direction of each electron is different, each electron should experience a different force and therefore be detected at different spots of screen. The problem was that the electrons are detected at two spots instead of a continuous distribution meaning there is something unusual about the spin distribution as if there are two possible quantum states for the spin. Additionally, the detected distribution is rotated as the magnate is rotated as if the spin distribution is dependent on the detection method.

(solution: influence by other effect): All spins are aligned inside the magnet in one direction along the magnetic field. The measured distribution of the spin direction is not isotropic spin- unpolarized as at the muzzle of the electron gun, but the fully-spin polarized as it is inside of the magnet.

(Incorrect Quantum explanation of Stern–Gerlach experiment): As a quantum- mechanical parameter, the direction of the electron spin cannot be defined exactly, but defined by a measurement. When measurement is from the right to the left ( the magnetic field increases from the right side to the left side ), the direction of electron spin can be only to the left or to the right. There are no up or forward or up/left directions. When the measurement direction is changed, the spin directions at the gun muzzle are magically change. For example, when measurement is from the down to the up ( the magnetic field increases from the bottom side to the top side), the direction of electron spin can be only to the up or to the down. There are no left or right or forward or up/left directions.

(Simple non- Quantum explanation of Stern–Gerlach experiment ): There is an additional effect, which the electron spin is experiences and which is ignored in the Quantum explanation. (additional ignored effect): The electron spin is aligned along the magnetic field.

video


One of best video describing details and history of Stern–Gerlach experiment	a nice and critical explanation of physics and conclusions (both correct and incorrect) of Stern–Gerlach experiment	my video of my view (2024)

Reproducing the Stern-Gerlach Experiment. ESI College Physics Film Program 1967

Reproducing the Stern-Gerlach Experiment with cesium atoms with a detailed step- by- step explanation of experimental setup and measurements.

Reproducing the Stern-Gerlach Experiment. ESI College Physics Film Program 1967

Explaination video

magnet

result

click on image to enlarge it

Spin Conservation Law against Quantum explanation of Stern–Gerlach experiment ->

(problems of the Quantum explanation)

(problem 1) The Quantum explanation violates the spin conservation law, which is well-verified law of the Physics. (problem 2) The Quantum explanation violates the Dirac equations; (problem 3) The Quantum explanation violates the observed direction of the time flow in our Universe

(problem 1) Spin conservation law

The conservation of the spin, which corresponds to the conservation of the time inverse symmetry.

The spin conservation law is similar and as strong as the energy conservation law.

The quantum explanation assumes that the spin direction is not defined and, therefore, is not conserved until the spin is measured. This assumption violates the fundamental spin conservation law.

(note): Each conservation law (e.g. the energy conservation law, the momentum conservation law) is originated from a specific symmetry of our Universe (See below). The energy conservation law is originated from the symmetry of continuos time flow. It means that all Physics laws will be same tomorrow as they are today. The spin conservation law is originated from the time- inverse symmetry. It means that all Physics laws will be same if the flow direction of the time is reversed. Therefore, the Energy and Spin conservation Laws are very similar and have very similar origins.

(incorrect claim of Stern–Gerlach experiment): The direction of the electron spins is determined by a measuring device. It means that the electron spin is not conserved and can change the direction influenced by a different measurement device. It is a fully incorrect claim, which severely violates the fundamental spin conservation law.

Perpetual motion machine cannot ever exist because of the energy conservation law

The energy conservation law does not allow to built a perpetual motion machine of any design

For hundreds years "engineers" and "scientists" are unsuccessfully challenging the fundamental energy law trying to built the perpetual motion machine.

Similarly, the fundamental spin conservation law are challenged by many scientists, which support the magical spin nature.

(problem 2) Dirac equations

The solution of the Dirac equations is a 4-rank spinor. However, a particle (an electron) is described by a scalar wave function. The 2 x functions describe a particle with opposite charge and 2x functions of the opposite spin. In order for spinor to become a wavefunction both the electron charge and the electron spin should be firmly fixed. As a result, any realistic particle (an electron or a positron) has the fixed charge -e or +e and the fixed spin (the fixed spin direction)

The statement, that the electron spin is not fixed, but defined by a measurement, is fully equivalent to the statement, that the charge of the electron is not fixed, but defined by a measurement.

(problem 3) Precise definition of the direction of the time flow in our Universe.

The requirement that the spin direction is precisely fixed also means that the direction of the time flow in our Universe is fixed.

At any moment of time, the electron has a possibility to have one of two wave functions. The first wavefunction corresponds to the forward time flow. The second wavefunction corresponds to the reversed time flow. From these two possible wave functions, the electron always has the first one, because the direction of the time flow is firmly fixed. The direction of the time flow is only in the forward direction. Assumption, that the spin direction is undefined, directly means the direction of the time flow is not defined.

Similarity of Energy Conservation Law and the Spin Conservation Law

The spin conservation law is as strict as the energy conservation law. The quantum explanation of the spin behavior in the Stern–Gerlach experiment clearly violates the spin conservation law.

According to the Noether rule, any conservation law originates from some symmetry. The energy conservation law is due to the time- continuity symmetry. The laws of Physics will be the same tomorrow as they are today. The spin conservation law is due to the time- inversion symmetry. The laws of Physics will be the same if the direction of the flow of the time is reversed. Therefore, the energy and spin conservation laws are so similar!!

(fact) It took more than 100 years for people to accept the fundamental energy conservation Law. Still now some people are trying unsuccessfully to fabricate a perpetual motion machine, which will provide energy infinitely. However, the fact is the energy conservation Law cannot be broken

I hope, someday the spin conservation law will be as respected as the energy conservation law is respected now.

Two options of design of a magnet with a gradient of magnetic field, which was used in the original Stern–Gerlach experiment

See magnet design in the original paper here.

It is difficult to guess the exact design of the magnet, which was originally used in the Stern–Gerlach experiment. There was a gradient of the magnetic field. A gradient of a magnetic field means that the magnetic field changes from one value to another value.

There are two options of design of a magnet with a gradient of magnetic field, any of which gives two detected lines (as was observed in the experiment!!):

(magnet option 1: radient of magnetic field does not change the polarity, but he polarity of the magnetic field changes): most probable

shown in Fig. 44 (click here)

In this case, there are two detected lines as particles with opposite spin directions are moved in opposite directions along the gradient.

In this case, the magnetic field changes from a minus value to a plus value along the magnet gap. E.g. at the left side of the gap at x=-a H=-H0 and at the right side of the gap at x=+a H=+H0. The gradient equals =H0/a The spins of particles, which enter the gap between x=-a and x=0, are aligned in the minus direction along -H. As a result, the particles are moved to the left along the gradient. The spins of particles, which enter the gap between x=0 and x=+a, are aligned in the plus direction along +H. As a result, the particles are moved to the right along the gradient. As a result, there are two detected lines!!!!

(magnet option 2: the magnetic field does not change polarity, but there are two opposite gradients.):: less probable, but simpler

shown in Fig. 45 (click here)

In this case, there are two detected lines as particles with opposite spin directions are moved in opposite directions along the gradient.

The simplest example of such a magnet is the magnet, which consists of two connected cylindrical poles with a gap at one side (the simplest case of a magnet). In this magnet, the magnetic field changes from zero value (far from magnet) to some value H ( at center between poles) and next back to zero (far from magnet in the opposite direction). The polarity of the magnetic field is the same, but there are positive and negative gradients. In this case all spins are aligned in one direction, but the opposite gradients again make two detected lines !!!!!

Is the spin a quantum parameter?

No. Similar to the energy, the spin is a general conserved parameter of an object. The spin describes the degree of the broken- time-inversion symmetry. Its quantization originates from two possible opposite directions of the time flow. Correspondingly, the broken time-inversion symmetry and, therefore, the spin have only two components: spin-up and spin-down.

The spin can manifest itself in the large world (a permanent magnet) and in small quantum world (spin- dependency of the energy levels of an atom)

Classical explanation of the Spin by Dr. Matt O`Dowt Video

Classical explanation of spin by Dr. Matt O`Dowt

Dirac and Non- Dirac representations of the Spin

(what is it about?): The spin of an elementary particle always represents the rotation between its two components of the quantum field or, the same, the broken time-inverse symmetry. The Dirac and Non- Dirac representations of the Spin are distinguished on how the rotation of the quantum field occurs in the 3D space.

(Dirac representation):

The spin direction is independent of the propagation direction of the quantum field

(Non- Dirac representation):

The spin direction field dependents on the propagation direction of the quantum field

The elementary particle, which spin is represented either by Dirac or Non-Dirac representation:

(note) For many elementary particles, it is difficult to verify experimentally which of either the Dirac or the Non-Dirac representation describes the particle spin.

(Non- Dirac representation):

(we know for sure): The spin of the photon and the the electromagnetic field is described by the Non- Dirac representation.

(note): From all quantum fields, the electromagnetic field is most understood, because all its properties can be measured directly.

(very probably): Neutrino and the quantum field of the weak interaction.

(note): The weak and electromagnetic fields are very similar and originated from a breaking of one single quantum field.

(Non- Dirac representation):

(very probably): The Electron

(note): The Dirac equation describes all properties of the electron and the electron quantum field rather well.

(it is more natural): In fact, the non-Dirac representation of the spin is more natural.

(Why is that?): The movement of the quantum field by itself breaks the time inverse- symmetry. When the direction of the time flow is reversed, the movement direction of the quantum field. Therefore, it is very natural that the breaking of the time- inverse symmetry for the quantum field is related to the breaking of the time- inverse symmetry due to the movement of the quantum field and, therefore, is related to the movement direction of the quantum field.

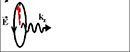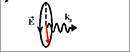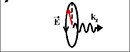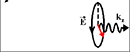In fact, for the electromagnetic field, which we have measured and studied most, the spin direction of a photon is always in the movement direction of the photon.

Dirac representations of the Spin

(key fact): In the Dirac representations of the Spin, the rotation direction between two components of the quantum field is independent of the propagation direction of the quantum field

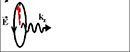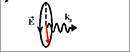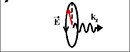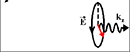In the Dirac representations of the Spin, the the axis of the rotation of the quantum field can be both along and perpendicular to the movement direction of the quantum field.

(it is very probably): that the Electron is described by the Dirac representation

Dirac representations of the Spin of an elementary particle with a rest mass

spin is along X- axis	spin is along Y- axis	spin is along Z- axis

The rotation direction of the quantum field is always along the X- axis for the quantum field propagating along the X- Y-, Z- axes.	The rotation direction of the quantum field is always along the Y- axis for the quantum field propagating along the X- Y-, Z- axes.	The rotation direction of the quantum field is always along the Z- axis for the quantum field propagating along the X- Y-, Z- axes.

In the Dirac representations of the Spin, the axis of the rotation direction between two components of quantum field is always directed along the spin direction independently of the propagation direction of the quantum field

A particle with a rest mass (for example, an electron) is represented as a massless quantum field of the electron, which is bounced back and forward between two mirrors. The energy of this confined state gives the electron rest mass. See above Einstein's representation of particle with a rest mass. The mirrors represent the Higgs field, from which the quantum field is continuously reflected in opposite direction. The size of an elementary particle is finite along all 3 directions. Therefore, the finite size in 3 directions can be represented by 3 pairs of the mirrors, which reflect the quantum field backward and forward in the X- Y- and Z- directions.

As the quantum field propagates from one side of the particle to another side, there is a rotation between the two components of the quantum field. The rotation breaks the time- inverse symmetry, which is described by the spin

click on image to enlarge it

Two components of the quantum field are describes by two components of a spinor.

Non- Dirac representations of the Spin

(key fact): In the Non- Dirac representations of the Spin, the rotation direction between two components of the quantum field is dependents on the propagation direction of the quantum field

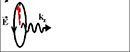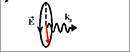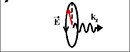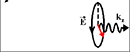In the Non- Dirac representations of the Spin, the the axis of the rotation of the quantum field is fixed with respect to the movement direction of the quantum field.

Non-Dirac representations of the Spin of an elementary particle with a rest mass

spin is along X- axis	spin is along Y- axis	spin is along Z- axis

There is a rotation between two components of the quantum field only when the quantum field moves along the x- direction. There is no rotation when the quantum field moves along either the y- or z- direction. When moving along the y- direction, the quantum field is described by its 1st component (e.g. the upper-raw wave function of the spinor). When moving along the z- direction, the quantum field is described by its 2nd component (e.g. the lower-raw wave function of the spinor).	There is a rotation between two components of the quantum field only when the quantum field moves along the Y- direction. There is no rotation when the quantum field moves along either the Z- or Y- direction. When moving along the Z- direction, the quantum field is described by its 1st component (e.g. the upper-raw wave function of the spinor). When moving along the X- direction, the quantum field is described by its 2nd component (e.g. the lower-raw wave function of the spinor).	There is a rotation between two components of the quantum field only when the quantum field moves along the Z- direction. There is no rotation when the quantum field moves along either the X- or Y- direction. When moving along the X- direction, the quantum field is described by its 1st component (e.g. the upper-raw wave function of the spinor). When moving along the Y- direction, the quantum field is described by its 2nd component (e.g. the lower-raw wave function of the spinor).

In the Non- Dirac representations of the Spin, the axis of the rotation direction between two components of the quantum field is firmly fixed with respect to the movement direction of the quantum field. As a result, the rotation of the quantum field exists only when the quantum field moves along a specific direction (with respect to the direction of the spin). Along the perpendicular movement direction, there is no rotation of the quantum field and the quantum field is described by one of its two components.

As the quantum field propagates from one side of the particle to another side, there may be a rotation between the two components of the quantum field. The rotation breaks the time- inverse symmetry, which is described by the spin

click on image to enlarge it

Two components of the quantum field are describes by two components of a spinor.

Dirac equations. vs Maxwell equations

(fact): The Dirac equation is the simplest description of a quantum field of an elementary particle, which has a rest mass, and whose broken time- inverse symmetry is described by the Dirac representation of the spin.

(note) In fact, the Dirac equation describes the quantum field of 4 components. A pair of two components correspond to a particle (the electron) and antiparticle (the positron). Only 2 components describe the broken time-inverse symmetry (the spin) for each the particle and the antiparticle.

(fact): The Maxwell equations are the simplest description of a quantum field of an elementary particle, which does not have a rest mass, and whose broken time- inverse symmetry is described by the non-Dirac representation of the spin.

(Complexity of Maxwell' equations) The Maxwell' equations are more complex, for example in comparison to the Dirac equations, because of the complexity to describe the dependence of the broken- time- inverse symmetry of the quantum field on the movement direction of the quantum field. Still Maxwell' equations is the simplest form to describe the Non-Dirac- type broken- time- inverse symmetry of the quantum field.

Why does the spin have a direction in space? Why doesn't the spin have only two states corresponding to "+" and "-" as similar as the charge has? Instead the spin has a spatial direction? Since the spin describes the time inversion, the "+" would correspond to the forward flow of time and the "-" would correspond to the backforward flow of time.

It is correct. The time inversion symmetry can be broken by two methods and, therefore, be described either by a spin scalar or a spin vector.

When the spin is a vector, the spin properties are somehow similar to the rotation. The broken rotation symmetry, which is described by the orbital moment, has also broken time-inverse symmetry, which is described by the vector. The direction of this vector corresponds to the rotation axis. (see here)

The example of the scalar spin is the spin of the photon. The spin of the photon may have only two possibilities (two directions). The spin can be either along or opposite to the direction of the photon propagation. Therefore, the spin of the photon is scalar, has only two possible values and, similar to the charge, the spin value can be assigned as "+" and "-" values.

Only the quantum field of the Non- Dirac representation of the Spin has the spin as a scalar.

An elementary particle with a rest mass of both the Dirac and Non- Dirac representations of the Spin has the spin as a vector.

An elementary particle without a rest mass of the Dirac and Non- Dirac representation of the Spin has spin as a vector.

Mechanical forces & Mechanical torque due to the Spin & Magnetic field

(fact) A single elementary particle with the spin experiences only one mechanical force in a magnetic field, while an assembly of the particles with spins, like a permanent magnet, experiences three different mechanical forces in a magnetic field

Electrical charge and electrical dipole in a homogeneous (constant) electrical field

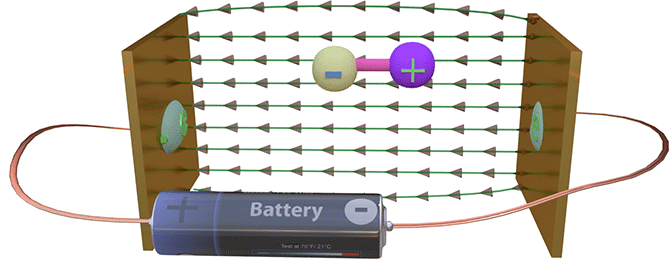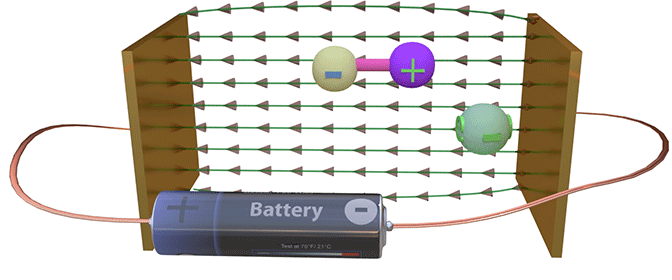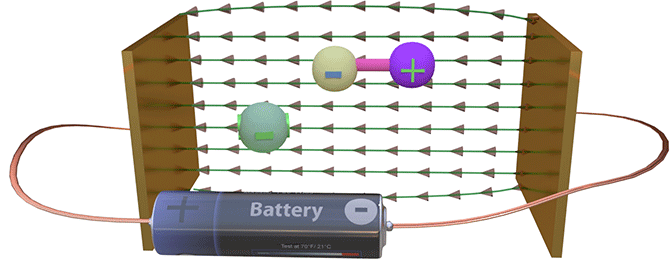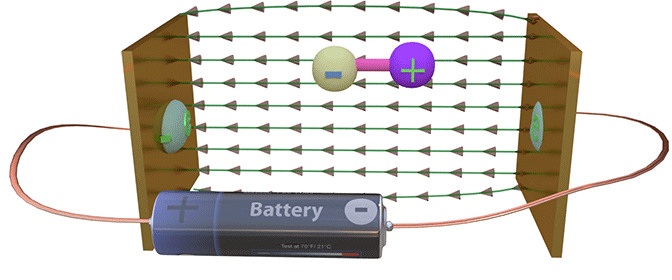(electrical charge): The electrical charge experiences a mechanical force in a homogeneous electrical field, which accelerates the electron movement from the negative to positive electrode.

(electrical dipole or electrical moment):: An electrical dipole does not experience any mechanical force in a homogeneous electrical field as if it does not exists

The electrical field is a constant between electrodes because of the same size of the electrodes

Click on image to enlarge it

Mechanical force, act on a single electron,

(only force) gradient of magnetic field

Mechanical force/torque, act on an assembly of electrons,

(force 1, strongest) gradient of magnetic field

(force 2, moderate) artificial magnetic charge. Compass torque.

(force 3) Einstein–de Haas torque

Q. Why mechanical force & torque are acting differently on a single electron and on an assembly of electrons?

As an elementary particle, the electron does not have parts. For this reason, it cannot have the north part , for example, at the left part and the south part at the right side. Both the south and north are distributed homogeneously and equally all over whole volume of the electron. Additionally, a single electron cannot experience different forces at its different parts. The electron experience the same mechanical force for its all parts. For example, the left part of electron cannot experience a different mechanical force than its left part. Since the electron does not have the parts, the left and right parts always experiences the same force.

In contrast, an assemble of electrons can experience different forces at different parts. For example, the electrons at the left part may experience the larger mechanical force than the electron at the right part.

Origin of the mechanical force

An object is forced to accelerate in space when object energy is dependent on its spacial position. For example, the object is forced to accelerated towards the left or, similarly, experiences a mechanical force towards the left, when the object energy is smaller when it is shifted to the left.

Electrical dipole in a inhomogeneous electrical field

An electrical dipole or an electrical moment experiences a mechanical force in a inhomogeneous electrical field, which accelerates movement of the electrical dipole towards a larger electrical field

The electrical field is smaller at the left (negative) electrode and larger at the right positive electrode because of different sizes of the electrodes

Click on image to enlarge it

(Mechanical force 1 (strongest)):Due to a gradient of magnetic field

According to the Laws of Mechanics, a force acts on an object in the direction, in which the total energy of the is minimized. The electron energy in a magnetic field is S*H/2.

In a gradient of magnetic field, a force acts on an electron. The direction of this force depends on the electron spin.

When spin is parallel to the magnetic field, the force acts so that electron moves in the direction from a smaller to a larger magnetic field.

When spin is antiparallel to the magnetic field, the force acts so that electron moves in the direction from a larger to smaller magnetic field.

(note) This force causes the repelling or attraction between two permanent magnets, which we may experience in everyday life.

Why and at which condition does a particle experience a mechanical force?

A particle experiences a mechanical force, when the particle energy depends on the particle special position. The particle is mechanically forced into the position where its total energy is smaller.

Why particle is forced to the position of a lower energy?

interpretation of the mechanical force:

(interpretation 1): classic quantum electrodynamics. Gaining a momentum

In a gradient of electrical field (e.g. from the left to right) , the number of virtual photons, which are absorbed from the left and from the right side, are different. Since each photon transforms a mechanical moment to the particle, the mechanical moment of the particle is changes and the particle is forced to accelerate.

(interpretation 2): quantum vibrations. Gaining energy.

Due to interaction with virtual particles, the elementary particle position is randomly changed in time. The change is extremely tiny and it is called the quantum oscillations. In the absence of the gradient of the field, the distribution of the virtual particle and, therefore, the quantum vibrations are fully symmetrical. as a result, the particle average position remains a constant. However, in the case when at one spacial point the particle energy is smaller and at another special point the energy is larger, the quantum vibrations became asymmetrical and the particle is forced to accelerate towards the larger quantum vibration.

A virtual particle of a fixed energy makes a quantum oscillation larger into region of a lower energy and a shorter in region of a higher energy. It is because the movement into the the region of the higher energy requires a virtual particle of a higher energy, which live time of the virtual particle is shorter and, therefore, the movement distance of the elementary particle shorter. This is the reason why the particle is forced to accelerate towards the region of the lower energy.

Mechanical force due to a gradient of magnetic field

Levitation	Gradient to the left	Gradient to the right

The "South" and "North" poles are of the same size. As a result, there is no gradient of magnetic field towards each pole and the small magnet is levitating in the center between them	The smaller area of "south" poles makes the magnetic field near "S" pole more denser and, therefore, larger. There is a gradient of the magnetic field. The magnetic field is smaller at "N" pole and larger at "S" pole .	The smaller area of "north" poles makes the magnetic field near "N" pole more denser and, therefore, larger. There is a gradient of the magnetic field. The magnetic field is smaller at "S" pole and larger at "N" pole
(*levitation*): The levitation point is middle between poles, where the density of magnetic field is largest. When the object moves out of the levitation point, it experiences a smaller magnetic field and its magnetic energy becomes smaller. The gradient of magnetic field forces the object back to the levitation point in order to increase the object magnetic energy	(mechanical force to the left) The object is forced to the left toward the smaller "S" pole, where the magnetic field is larger and, therefore, the object magnetic energy is larger.	(mechanical force to the right) The object is forced to the right toward the smaller "N" pole, where the magnetic field is larger and, therefore, the object magnetic energy is larger.

A small magnet, which have a magnetic moment, in a magnetic field created by two poles of a larger magnet.

There is a gradient of magnetic filed in the space between two poles. An object with a magnetic moment experiences a mechanical force from the gradient, which forces the object to the spacial point where the magnetic field is the largest.

Fig.45 click on image to enlarge it

(Levitation):

When an object with a magnetic moment is placed in a local maximum of magnetic field, the object is forced to stay there. In the case when the object moves out of the levitation point towards a region of a smaller magnetic field, its magnetic energy decrease. As a result, there is a mechanical force which moves the object back to the levitation point.

(Mechanical force 2 (moderate) ): Due to an artificial magnetic charge. The mechanical force of compass pointer.

(fact) An elementary particle cannot have a magnetic charge. An elementary particle only can have an electrical charge and/or a magnetic moment.

Mechanical force of compass pointer

(Mechanical force in a homogeneous magnetic field)): There are artificial magnetic charges at each tip of the compass arrow. Each magnetic charge experience a mechanical force in a homogeneous magnetic field, which is created by the large magnet. The "N" magnetic charge is attracted to "S" pole of the large magnet. The "N" magnetic charge is attracted to "S" pole.

(mechanical torque)): Neither amplitude nor direction of the mechanical force changes, when compass arrow rotates. However, the mechanical torque, which aligns the compass arrow along the magnetic field..

Click on image to enlarge it

(reason) why an elementary particle cannot have a magnetic charge

Any property of an elementary particle corresponds to a breaking of a very specific symmetry of the time-space of our universe. The electrical charge corresponds to the breaking of the gauge symmetry, the spin corresponds to the breaking of the time-inverse symmetry and the magnetic moment corresponds to the breaking of the breaking of both the time-inverse symmetry and the gauge symmetry (See here)

There is no symmetry, the breaking of which, could create the magnetic charge.

(fact) A single elementary particle cannot create an artificial magnetic charge.

(fact) An assembly of elementary particles with spin can create an artificial magnetic charge at a boundary of the assembly.

How to distinguish an existence of a magnetic charge?

If an assembly of particle has a magnetic charge inside, it will experience a mechanical force in a homogeneous magnetic field (a constant magnetic field).

If an assembly of particle does not have a magnetic charge inside, there is any mechanical force on the assembly when it is in a homogeneous magnetic field .

Magnetic charge is also called a pole. The two opposite magnetic charges are called the "North pole" and "South pole".

(fact) (rotation torque vs. linear force) Conventional understanding is that the compass arrow experiences a mechanical torque in a magnetic field. However, the compass arrow can experience a linear force in one direction. For example, if the external magnetic field chance its direction at positions of "N" and "S" magnetic charges.

Difference of spin-related magnetic moment of a single electron and a bulk object

Bulk magnet (right): There are specially- separated regions of "N" magnetic charge (shown in blue color) and and of "S" magnetic charge (shown in red color)

A single electron (left): As an elementary particle, an electron cannot have separated parts. As a result, the electron does not have specially- separated "N" and "S" regions and the "S" and "N" regions are homogeneously distributed over the volume of the electron.

See about size and volume of a single electron here

Click on image to enlarge it

Artificial magnetic charge: (origin)

The artificial magnetic charge or the magnetic pole is originated in an assemble of electrons with aligned spins, when the electron magnetic moment is only partiality compensated by magnetic moments of its neighbor electrons. The magnetic moment is not fully compensated at edge of the sample along direction of aligned magnetic moments.

Each localized electron has a magnetic moment, but it does not have a magnetic charge. Each "S" pole is in contact with "N" pole of a neighbor electron and, therefore, the "S" pole is compensated, the "N" pole is not compensated by this electron. Similarity, if there is an electron at other side, each "N" pole is compensated by "S" pole of the neighbor electron at other side. At the edges of the bulk nanomagnet, there is no compensation. As a result, the artificial magnetic charge (a magnetic pole) is formed at the edges.

How large the artificial magnetic charge?

Does artificial magnetic charge exists in an antiferromagnetic material?

Compass arrow and artificial magnetic charge:

A bar of ferromagnetic material, which is fixed on a rotation axis and can be rotated around this axis under an external force, aligned itself along an external magnetic filed (e.g. Earth magnetic field). The ferromagnetic bar experiences the mechanical torque due to the magnetic charges (magnetic poles) on sides of the bar. The mechanical force acts on the magnetic charges from the external magnetic field causing the mechanical torque.

In contrast to a single electron, the compass arrow experience a magnetic force in a homogenous (constant) magnetic field.

(fact ) (difference between magnetic moments of an electron and compass error)

The electron does not have any magnetic charge or magnetic poles. The electron only has a magnetic moment. In contrast, the compass arrow has two opposite magnetic charges (poles) on its sides, which are separated by a substantial distance. Such configuration of opposite magnetic charges makes a magnetic moment. Therefore, the primary property of the compass arrow is the magnetic charge. The magnetic moment is the result of specific configuration of the magnetic charge

Artificial magnetic charge created at the edges of magnet

Bulk magnet ( shown as a transparent box) contains of a stack of aligned magnetic moments of localized electrons ( shown as red/blue magnets). At edges of the bulk magnet, the artificial magnetic charge or a magnetic pole is created (shown as balls). At the left side, the "N" artificial magnetic charge (pole) is created (shown as red ball). At the right side, the "S" artificial magnetic charge (pole) is created (shown as blue ball).

Due to the artificial magnetic charge, the bulk magnet experiences a mechanical force in a homogeneous magnetic field.

Each localized electron has a magnetic moment (shown as blue/red bars in figure), but it does not have a magnetic charge. Each "S" pole is in contact with "N" pole of a neighbor electron and< therefore, it is compensated. Similarity, Each "N" pole is compensated by "S" pole of the neighbor electron. At the edges of the bulk nanomagnet, there is no compensation. As a result, the artificial magnetic charge (a magnetic pole) is formed art the edges.

Even though each individual electron does not experience a mechanical force in a homogeneous magnetic field. An assembly of exchanged coupled electrons experience a mechanical force in a homogeneous magnetic field.

Click on image to enlarge it

(Mechanical force 3 (weakest) ): Due to Einstein–de Haas effect.

wiki page is here

See classical explanation below in Dr. Matt O`Dowt video time: 0:24

This torque occurs due to a change of the rotational moment of an object, when the total spin of the object is change.

(case 1) changing of domain structure

A relatively- large ferromagnetic object (sizes > domain size) has a multi- domain structure and its total spin is close to zero. In an external magnetic field, the magnetic domains are realign in one direction and the total spin of the object becomes a substantial. The rotation moment related to the spin become larger,, but the total orbital momentum of the object should not change due to the domain rearrangement. As a result, the whole bulk object gains

What is the magnetic field?

3 origins of the magnetic field.

(Origin 1 of magnetic field ) Relativistic component of the electromagnetic field

(source of magnetic field): electrical charge

Magnetic field of source 1: magnetic field generated by an electromagnet

Magnetic field in an electromagnet is generated by the electron current flowing in a metallic wire.

Electromagnetic field has two components; electrical field and magnetic field, which relativistically transformed to each other. The magnitudes of the observed components of the electric and magnetic fields dependent on the speed of an observer. E.g. if in the first coordinate system an observer experiences only an electrical field, but no magnetic field, in coordinate system, which is moving with respect to the first coordinate system, the observer experiences both the electrical and magnetic fields. The transformations between field are described by the the Lorentz transformation rules as

where E_static, H_static are the electric and magnetic field in the static coordinate system (reference frame) and E_move, H_move are the electric and magnetic field in the coordinate system, which moves with a constant speed v.

This magnetic field is originated from the nature of the electromagnetic field itself. There are two effects due to this source of the magnetic field

(effect 1): Ampère's law

The Ampère's law describes the fact that an electron current creates a magnetic field.

Relativistic origin of the Spin-Orbit Interaction

An electron (shown in red) is moving in a static electric field. In the coordinate system moving together with the electron, the static electric field is relativistically transformed into the effective electric field E_eff and the effective magnetic field H_eff. The H_eff is called the magnetic field of the spin-orbit interaction.

The charge of the electron creates an electrical field. There is no magnetic field component of this field only coordinate system, which the electron does not move. When the electron move, the electrical field, which has only the electrical-field component in the coordinate system moving together with the electron, has both the electrical-field and magnetic-field components in a static coordinate system.

(effect 2): Spin-orbit interaction

The spin-orbit interaction describes the fact that an electron, which moves perpendicularly to an electrical field, experience a magnetic field and the electron spin is aligned along that magnetic field.

See here more details about the spin-orbit interaction.

Even though there is only an electrical field there is no a magnetic field in a static coordinate system, there is a magnetic field in a coordinate system moving together with the electron and this magnetic field interacts with the electron spin.

Dependence on electron movement speed

Magnetic field of source 1 increases, when the electron moves faster

(Origin 2 of magnetic field ) magnetic moment due to the spin of electron

(source of magnetic field ): electrical charge+ broken time-inverse symmetry +

Magnetic field of source 2: magnetic field generated by a permanent magnet

In a permanent magnet the electron spins are aligned in one direction. Each such electron has a magnetic moment due to its spin. The sum of all aligned magnetic moments creates magnetic field of a permanent magnet.

Due to its spin and its charge, the electron has a magnetic moment, which generates a magnetic field

An elementary particle, which has a non-zero spin and non-zero charge, has a non-zero magnetic moment, which induces a magnetic field around the electron.

(note) The electron has a spin, because its time-inverse symmetry is broken. The electron has a charge, because its gauge symmetry is broken. Simultaneous breaking the time-inverse symmetry and the gauge symmetry creates a magnetic moment for an elementary particle (See here for more details)

(Zero spin + non-zero charge) spin-inactive electron no magnetic moment

For example, the electron of filled orbitals are charged, but their spin is compensated, has no magnetic moment. Formally the time-inverse symmetry is not broken for these electrons and therefore they have no spin.

(Non-zero spin + zero charge) 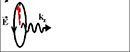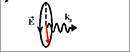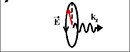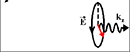circular- polarized photon no magnetic moment

For example, the spin of a circular- polarized photon is 1, but the the photon has no charge. As a result, the photon has no magnetic moment and does not produce any permanent magnetic field. Of course, the electromagnetic field of a photon has a magnetic component.

Dependence on electron movement speed

Magnetic field of source 2 decreases, when the electron moves faster

It is because the electron electron charge decreases with a faster speed. Since the magnetic moment is proportional to the electron charge, the magnetic moment decreases as well. A particle, which moves at speed of light, can not be charged and therefore cannot have a magnetic moment. It is a feature of the gauge symmetry.

(Origin 3 of magnetic field ): spin- dependent Coulomb interaction (exchange interaction)

(source of magnetic field ): broken time-inverse symmetry

Two electrons of opposite spins, when combined, form an elementary particle without spin.

Each quantum state can be occupied by two electrons of opposite spins. When a quantum state is occupied by one electron, it is an elementary particle with charge -e and spin=1/2, When a quantum state is occupied by two electrons, it is an elementary particle with charge -2e and spin=0
click on image to enlarge it

The Coulomb interaction between electrons depends on their mutual direction of their spins. It makes the electron energy dependent on its spin direction. There is a spin direction, at which the electron energy is smallest and which is the equilibrium spin direction. There is a spin precession for any any different spin direction and spin damping align the electron spin along its equilibrium direction. All these features are exactly the same of the case of the magnetic field of origins 1 and 2. Therefore, the exchange field can be assigned as a magnetic field of origin 3.

(note) Even though the exchange field is completely different from the relativistic magnetic component of the electromagnetic field, which is usually associated with a magnetic field, in a solid its feature are nearly- indistinguishable from features of the conventional magnetic field. It is convenient to handle the exchange field in a solid as a magnetic field. For example, the features and properties of antiferromagnetic resonance, which is created by the exchange field, are very similar to that of the ferromagnetic resonance (FMR), which is created by the conventional magnetic field.

(effect ): Exchange interaction

The exchange interaction describes the spin-dependent Coulomb interaction between electrons. The Coulomb repulsion between two electrons is smaller, when their spins are opposite, and is larger, when their spins are parallel. When two electrons of opposite spins approach each other, the breaking of time- inverse symmetry slowly disappears and system of two elementary particles transforms into a system of one particle. As a result, their mutual repulsion decreases and their interaction with surrounding electrons and nuclei is changed

The time-inverse symmetry is not broken for an electron state, which occupied by two electrons of opposite spins. It literally means that such state does not have any spin at all. It also means that the state should be considered as one particle without spin with charge -2e instead of two electrons with opposite spins and charge -e and -e. When two electrons of opposite spins approach each other, they are monotonically transformed from the system of elementary particles into a system of only one elementary particle. As a result, the Coulomb repulsion between these two electrons monotonically decreases and the Coulomb interaction between each and surrounding electrons and nuclei is changed.

Dependence on electron movement speed

Magnetic field of source 3 is independent of the electron movement speed.

The exchange interaction only depends on the distance between electrons and their spin direction.

3 types of the magnetic field: (1) conventional magnetic field; (2) Spin-orbit magnetic field; (3) magnetic field of the exchange interaction.

3 types of magnetic field

Type 1: Conventional magnetic field	Type 2: Magnetic field of Spin-orbit interaction	Type 3: effective magnetic field of the exchange interaction

This is the conventional magnetic filed. This magnetic field "fills" all the space and all electrons experience equally this magnetic field.	The magnetic field H_SO of the spin- orbit interaction is the component of the electromagnetic field similar to the conventional magnetic field. However, each electron experiences an individual H_SO of different magnitude and direction. The H_SO of each electron does not influence the spin any neighbor electron. Even electrons, which rotate around the same nucleus, may have different H_SO when their orbital symmetry is different.	In the exchange field the electron spin is aligned either parallel or anti parallel to the spin direction of its neighbor electrons. The exchange field is not a component of the electromagnetic field. However, in a solid the spin properties of the electron in a exchange field are exactly the same as in a conventional magnetic field. Therefore, the exchange field can be assigned as an effective magnetic field.
	The H_SO is originated from electric field of a nucleus and depends on the orbital symmetry of the electron. That is why the H_SO is individual for each electron. Details about the spin-orbit interaction are here.	Details about the exchange interaction are here

The spin properties of electrons are exactly the same for each type of the magnetic field. In an equilibrium the electron spin is aligned along the total magnetic field, which is a vector sum of all three types of the magnetic field. There is a spin precession before the alignment.

click on image to enlarge it

Proton and Neutron. Spin and Magnetic moment.

proton spin is 1/2; neutron spin is 1/2

The magnetic moment of a proton, measured in nuclear magneton units, is +2.79285. The magnetic moment of a neutron is −1.9130.

The magnetic moment of a neutron is −1.9130 μ_N. The ratio of magnetic moments of proton and neutron is −0.685 μ_N, intriguingly close to −2/3. There is only a 2.7 percent difference. This suggests that the ratio of the intrinsic magnetic moments of the neutron and proton might be precisely −2/3.

where 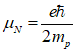is the nuclear magneton. This value represents the magnetic moment of an elementary particle with a mass equivalent to that of a proton and a charge of a proton +e. Given that the magnetic moment of a proton differs from m, it suggests that the proton is not an elementary particle but rather a particle composed of three elementary particles (three quarks).

(note): magnetic moment of a proton is about 1500 times smaller than the magnetic moment of an electron (Bohr magneton), because of equally larger mass of the proton.

Proton consists of 2 up quarks and 1 down quark

Neuron consists of 1 up quark and 2 down quarks

Up quark: electrical charge +2/3 e; spin =1/2

Down quark: electrical charge -1/3 e; spin =1/2

electrical dipole moment of neutron and proton.

Does the neutron have an electrical dipole moment?

Since the neutron consists of 3 electrically- charged quarks, the neutron should have a nonzero electric dipole moment, but seventy years of efforts to measure the neutron's EDM have been consistent with zero at higher and higher precision. (see here)

Is there charge inside the neutron? Given that the electrical dipole moment hasn't been detected in the neutron, all quarks with different charges may reside in the same location within the neutron, thereby precluding the creation of any electrical dipole.

It is possible, but unlikely.

The neutron possesses a magnetic moment of -1.9130 μ_N. The presence of an electrical charge and the breaking of time-inverse symmetry are two necessary conditions for a particle to exhibit a magnetic moment. Time-inverse symmetry is broken when a particle possesses spin and/or orbital momentum. Comprising three quarks, it's plausible for them to coexist in the same location but with different spin and orbital momentum orientations, thereby generating the neutron's magnetic moment. However, this scenario is considered unlikely

Measurements of electrical dipole moment:

(direct measurement) : A measurement of a force, which a neutron experiences in a gradient of an electrical field.

(indirect measurement): A measurement of the Larmor precession of the neutron spin in the presence of parallel and antiparallel magnetic and electric fields. The method is based on an unverified assumption that the magnetic and electric dipole moments in the neutron are locked to each other.

Losing of electrical charge and magnetic moment for neutrons and quarks in the deep core of a neutron star and inside a black hole

Under intense gravitational forces within the deep core of a neutron star or inside a black hole, the symmetry governing electrical charge becomes unbroken. Consequently, neutrons and quarks lose their electrical charge and become electrically neutral.The magnetic moments of neutrons diminish.

Questions & Answers

(about Misinterpretation of the Stern–Gerlach experiment)

There is an alternative interpretation of the Stern-Gerlach experiment that does not violate any fundamental laws of physics and does not rely on "quantum magic" explanations. It is crucial to note that the experiment's results are influenced by two effects.

The first effect is a mechanical force along a gradient of the magnetic field that moves a particle along the gradient. The force's direction and strength depend on the particle's spin direction with respect to the gradient, with particles of opposite spin directions moving in opposite directions.

The second effect is the alignment of the spin along the direction of the magnetic field, regardless of gradient. In any magnetic field, there is a spin precession and, consequently, a spin precession damping. As a result of the spin precession damping, the spin aligns along the magnetic field direction. The spin alignment occurs very quickly.

When a beam of particles with any complex distribution of spin directions enters a magnetic field, the spins of all particles quickly align along the magnetic field direction. As a result, all particles experience an equal mechanical force, leading to a line shape in the detected pattern.

Two detected lines result from a polarity change of either magnetic field or a gradient of the magnetic inside the gap of the magnet.

There are two options of design of a magnet with a gradient of magnetic field, any of which gives two detected lines:

(magnet option 1): gradient of magnetic field does not change the polarity, but he polarity of the magnetic field changes

This case of magnet shown in Fig.44 above

In this case, there are two detected lines as particles with opposite spin directions are moved in opposite directions along the same-polarity gradient.

(magnet option 2): the magnetic field does not change polarity, but there are two opposite gradients.

This case of magnet shown in Fig.45 above

In this case, all spins are aligned in one direction, but the opposite gradients produce two detected lines.

(the reason why the detected lines are rotated when the magnet is rotated):

It is not because the spin direction is not defined and, therefore, is not conserved until the spin is measured. The spin is always well defined and well conserved.

When the magnet is rotated, the detected lines are also rotated because both the magnetic field gradient and the regions of opposite polarities are rotated with the magnet.

(the spin conservation law):

The spin conservation law originates from the time-inversion symmetry

It is essential to note that the spin conservation law is as strict as the energy conservation law, and the quantum explanation of the spin behavior in the Stern-Gerlach experiment violates the spin conservation law.

(about spin-mixed state)

Does a spin-mixed state exist? Is the spin-mixed state just a simple sum of spin-up and spin-down electrons? Can you comment on properties of a spin-mixed state?

No. The spin-mixed state can not exist in reality. The spin-mixed state is a trick used sometimes in some theoretical approximations. The spin describes a breaking of the time inverse symmetry. The time inverse symmetry cannot be broken partly. The time inverse symmetry is either broken or not. The time inverse symmetry is broken, when a quantum state is occupied by one electron. Such a state is spin active. The time inverse symmetry is not broken, when a quantum state is occupied by two electrons. Such a state is spin inactive.

The spin can be either along (spin-up) or opposite (spin-down) to the direction of the broken time inverse symmetry. Only another possible and allowed state for the spin (or any subject of the broken time-inverse symmetry) is the spin precession state. The spin precession is a superposition of the spin-up and spin-down state, but it is not a spin-mixed state. Besides, the spin-precession state is not a static state. During the spin precession a photon or a magnon is unavoidably emitted and the spin is aligned along the up- direction.

Also, either spin-up or spin-down can be decomposed into components ( e.g. into a sum of spin-left and spin-right components). Such a sum of spin-left and spin-right components is not a spin-mixed state as well.

(about electrical charge reduction for a moving electron)

(from femtokitty): In origin-2 of magnetic field, when you say that the magnetic field decreases with increasing speed of electron. And justify it by saying that the electron charge reduces with increasing speed. I do not understand how electron charge can reduce with increasing speed. Is it a relativistic phenomena? where can i read more about this?

Yes, you are correct. It is a relativistic effect.

(Dirac Equation under Lorentz transformation)

The relativistic behavior of an electron is mathematically described by the Dirac equation, which exhibits symmetry under relativistic transformations. A solution of the Dirac equation takes the form of a 4th-rank spinor, indicating that it consists of four distinct wavefunctions. Two of these wavefunctions represent opposite spin directions, while the other two describe the positron or electron state of the electron quantum field An electron with a particular spin direction is described by only one of the four wavefunctions; the remaining three are zero.

Undergoing a relativistic or Lorentz transformation, these four wavefunctions become mixed. The electron wavefunction acquires all remaining components, which includes the positron components and the component of the opposite spin, implying that neither charge nor spin is conserved throughout the Lorentz transformation.

It literally means that when an electron moves, additionally to its electron part of the quantum field, the electron has a positron part of the quantum field. As electron velocity increases, the proportion of the positron component quantum field becomes larger in the electron quantum field. However, it's important to note that this doesn't mean a positron physically attaches to the electron. Rather, the charge of the electron diminishes, while it retains its fundamental electron nature, albeit with a reduced charge.

(Gauge symmetry under Lorentz transformation)

Any property of an elementary particle corresponds to a breaking of some specific symmetry of the space- time. The electrical charge of an elementary particle corresponds to the breaking of gauge symmetry meaning the breaking of the phase symmetry of an electron wavefunction. There are more details about this here.

It is important that the gauge symmetry cannot be broken abruptly. It requires some spatial distance over which the phase symmetry of an electron wavefunction monotonically varies. The spatial distance corresponds to the length of the electron.

When the electron moves at a speed close to the speed of the light, this distance changes. Consequently, the degree to which gauge symmetry is broken diminishes, resulting in a reduction in the electron's electric charge.

(absence of an electrical charge for a massless particle)

Due to the same underlying principle, a massless elementary particle cannot possess an electrical charge. The reason lies in the fact that a massless particle constantly travels at the speed of light, and as such, it lacks the necessary spatial extent over which gauge symmetry can transition from one value to another, thereby generating electrical charge.

In contrast, the breaking of time inverse symmetry, associated with particle spin, does not depend on any spatial dimension. Time can flow only either forwards or backwards, representing a binary condition without requiring spatial variation. Consequently, massless elementary particles may indeed possess spin. Two opposite spin directions correspond to the clockwise and counterclockwise rotations of the Quantum field.

It's noteworthy that all known massless particles, including photons and gluons, do not have electrical charge while possessing the spin.

(Electrical charge & Einstein model of an elementary particle with a rest mass)

According to the Einstein model, any elementary particle with a rest mass consists of a massless particle of the Quantum field reflected back and forward by the Higgs field.

Even though the massless particle itself does not have the charge, within this confined distance formed by the forward and backward moving massless particle, the gauge symmetry can vary enabling the electrical charge of the particle with the rest mass.

(Quantization of the electrical charge)

While the quantization of spin appears quite natural, the quantization of electrical charge is a more intricate concept. The quantization of the spin arises from the nature of time, which can flow only either forward or backward. It corresponds to two opposite values of the spin, leading to the inherent quantization of spin. In contrast, the gauge symmetry or the phase of a wavefunction can undergo continuous changes, allowing for electrical charge to assume any value without quantization.

The quantization of the electrical charge originated from the Einstein model. The gauge symmetry needs a distance to change. Such a required distance is present in particles with rest mass due to the continuous back-and-forth reflections of the quantum field between "Giggs mirrors". This continuous reflection imposes a constraint: the total phase shift after completing one full path must equal 2π times an integer value. This crucial condition restricts the potential variations in the wavefunction phase and results in the quantization of the electron's charge.

I am strongly against a fake and "highlight" research

Dr. Vadym Zayets

v.zayets(at)gmail.com

more Chapters on this topic:

more Chapters on this topic:

more Chapters on this topic:

Spin and Charge Transport

Abstract:

The spin is a quantity, which describes the degree of the broken time inverse symmetry for an elementary particle. If additionally the elementary particle has an electrical charge, there is a magnetic moment associated with the spin and the elementary particle interacts with the magnetic field.

Content

click on the chapter for the shortcut

() Spin of a photon

() Origin of the magnetic moment and symmetry

() Visualization of the spin & orbital moment

() Spin vs. Orbital moment. Time- inverse symmetry vs. rotational symmetry

() Interaction of the spin & orbital moment

() How to distinguish the spin from the orbital moment

() Dirac representations of the Spin

() Non- Dirac representations of the Spin

() Dirac equations. vs Maxwell equations

() Why does the spin have a direction in space?

() spin of a particle with a rest mass and massless particle