(merit 1): Eliminating the need for high crystal quality:
In semiconductor-based transistors, crystal periodicity is crucial as it creates the band gap necessary for operation. Maintaining high crystal quality becomes challenging in 3D integration due to the complexities of multi-layer fabrication. In contrast, the proposed all-metal transistor can be fabricated from polycrystalline or amorphous materials, which retain their quality over multiple layers, making them more suitable for 3D integration.

(merit 2): Size downscaling:
Traditional Si-based MOSFET transistors are approaching their physical downscaling limits. The proposed transistor, however, is constrained only by the minimum size of its magnetic domains, which can be as small as a few nanometers. Furthermore, as the size of the electrodes and magnetic domains decrease, the On/Off ratio of the transistor improves. This enhanced performance with smaller dimensions makes it ideal for further size reduction and integration into dense 3D architectures.

(merit 3): Lower operating voltage, reduced power consumption and the ability to withstand a high current.
Semiconductor transistors operate at voltages near the material’s band gap. For example, Si has a band gap of 1.1 eV, resulting in operating voltages around 1 V. This relatively high voltage limits power consumption reduction in semiconductor transistors. In contrast, the proposed all-metal transistor, which does not rely on a band gap, can operate at much lower voltages, leading to lower power consumption and the ability to handle higher current without performance degradation.

Why could an all-metal transistor be superior to a semiconductor transistor?:

FeBTb nanowire with Pt periodic electrode.

Periodic Pt electrodes on a ferromagnetic nanowire, which induces the periodical PMA in the wire. The front Hall probe contacts the region under the Pt electrode. The back Hall probe contacts the region in the gap between Pt electrode. Check below for the explanations. click on image to enlarge it

(reason 1) Simplified Materials and Fabrication.

The all-metal transistor can be fabricated using only metal and dielectric materials, without the need for semiconductors. This allows for the use of cost-effective techniques like sputtering and lift-off, avoiding the expensive processes required for semiconductor fabrication, such as epitaxial growth..

(reason 2) High Current and Temperature Endurance:.

Metals can withstand higher currents and temperatures than semiconductors. The electrical properties of metals are only minimally affected by temperature changes, while the electrical constants of semiconductors vary significantly with temperature. Additionally, metals have much lower resistance than semiconductors, enabling them to handle larger currents more efficiently.

(reason 3) Scaling Potential:

(merit 1): Contact resistance:

In contrast to semiconductor- semiconductor and semiconductor- metal contacts , the resistance of a metal-metal contact is very small and does not limit the ability to scale down the transistor in size.

(merit 2): Bulk resistance:

The inherently low bulk resistance of metals, compared to semiconductors, allows for a reduction in wire diameter without significantly increasing its resistance.

(reason 4) Faster Operational Speed:

The speed of a MOSFET transistor is constrained by the limited conductivity (mobility) of silicon, which is difficult to improve. Metals, on the other hand, have much higher conductivity, allowing all-metal transistors to operate at significantly faster speeds.

(reason 5) Use of Polycrystalline and Amorphous Materials::

MOSFET transistors require single-crystal silicon to achieve the necessary mobility. In contrast, all-metal transistors can be made from polycrystalline or amorphous materials without a reduction of the mobility, eliminating the need for expensive equipment to grow and protect single-crystal materials.

(reason 6) 3D Integration::

In 3D integration, new layers of transistors are fabricated on top of existing layers. The performance of the transistors should remain consistent as more layers are added. For MOSFET transistors, maintaining quality in upper layers is challenging, as single-crystal materials cannot be grown on top of polycrystalline layers. Since all-metal transistors are made from polycrystalline or amorphous materials, their quality remains unaffected regardless of the number of layers, making them well-suited for 3D integration.

electronic and data - processing devices made of only metals: 2 approach

without usage of semiconductors

There are fundamental differences between semiconductors and metals, and these differences impact the feasibility of creating key data processing elements, such as bipolar and MOSFET transistors and laser diodes. It is important to explore whether these critical components, traditionally made from semiconductors, could also be fabricated from metals.

It is quite challenging to fabricate conventional electronic and computing components—such as Laser Emitting Diodes (LEDs), Field-Effect Transistors (FETs), and Bipolar Transistors—using only metals without the involvement of semiconductors.

(this is important:) This highlights the importance of exploring new operational principles for such devices in order to pave the way for fully metal-based electronics and computing systems.

Two potential approaches for fabricating electronic and data-processing devices using only metals:

(approach 1): Adapting Similar Operational Principles Used in Semiconductor Devices:

This approach involves applying the same fundamental principles and designs currently used in semiconductor-based devices to metal-based systems. The goal is to replicate the functionality of existing devices, such as transistors and LEDs, by modifying materials and mechanisms to suit metal-based architectures.

(approach 2): Developing Entirely New Operational Principles::

This approach explores novel concepts and mechanisms that have not been utilized in semiconductor-based devices. These new principles would be specifically designed to leverage the unique properties of metals, potentially leading to innovative types of electronic and data-processing devices that operate in fundamentally different ways from their semiconductor counterparts. One such unique property of metals is ferromagnetism, along with the associated phenomenon of magnetoresistance.

All- Metal Devices Adapting Similar Operational Principles Used in Semiconductor Devices

(device 1): Laser Emitting Diode (LED) made of only metals

(conventional semiconductor LED): In a semiconductor LED, the device is typically composed of p-type and n-type regions. When a voltage is applied, holes and electrons are injected into the same region, where they combine and emit photons as the laser output.

(all-metal LED): Two metals are separated by an oxide layer. When a voltage is applied, electrons and holes tunnel through the oxide between metal layers and recombine, producing photons as the laser output, potentially allowing for an all-metal LED.

LED made of only metals

conventional semiconductor LED	Can an LED be made entirely from metals?	all-metal LED

Under applied voltage, holes and electrons are injected into an undoped layer and combine creating photons.		When a voltage is applied, the Fermi levels of each two metals shift relative to each other. Electrons are tunneled from the first-side metal into the central metal, while holes are tunneled from the second-side metal into the central metal. As these electrons and holes recombine, photons are emitted.

click on image to enlarge it. Zayets 2024

Can an LED be made entirely from metals?

A. In principle, a similar approach as in a semiconductor LED could be applied for an all- metal LED. The electrons and holes constantly combine inside metal in great numbers. When two metals are separated by an oxide layer, electrons and holes tunnel through the oxide between metal layers and recombine, producing photons, which could be potentially used as the laser output allowing for an all-metal LED.

Operation of semiconductor LED. Direct Gap vs. Indirect Gap Semiconductors

LED band requirements

Direct Band semiconductor (e.g. GaAs)	InDirect Band semiconductor (e.g. Si)	Metal (e.g. Au). Single band
there is light emission	no light emission	no light emission

(Operational principle of a semiconductor LED):. When a voltage is applied, , the electron energy becomes high in the n- region and low in the p- region. As a result, electrons are injected into the conduction band from the n-type layer (on the left), while holes are injected into the valence band from the p-type layer (on the right). Alternatively, electrons are removed from the valence band into the p-type layer, leaving behind holes. Rapid electron scattering within each band causes electrons to quickly move to the bottom of the conduction band and holes to the top of the valence band. When an electron transitions from the conduction band to the valence band, it emits a photon with energy equal to the bandgap energy and a very small momentum. This process forms the basis of light emission in a semiconductor LED.	In the case of an indirect-gap semiconductor, the electrons at the bottom of the conduction band (higher energy band) and the holes at the top of the valence band (lower energy band) have different wavevectors (or momenta). Since photons have very small momentum, a direct electron transition from the conduction band to the valence band, accompanied by photon emission, is not possible due to the lack of the conservation of momentum. For this transition to occur, a particle with a larger momentum must be involved. A phonon (shown in green), which carries substantially larger momentum for the same energy, facilitates the transition. The electron transition in an indirect-gap semiconductor requires the participation of a phonon, which either generates or undergoes inelastic scattering to conserve momentum and allow the electron transition from the bottom of the conduction band to the top of the valence band. Light is not emitted in this case.	When a voltage is applied across three metal regions, the electron energy becomes higher in the metal on side 1 and lower in the metal on side 2. As a result,high-energy electrons are injected from the metal on side 1, while low- energy holes are injected from the metal on side 2. Due to very fast electron scattering within the bands, the high-energy electrons rapidly move down, and the low-energy holes quickly move up. This scattering ensures that the electrons and holes maintain a near-equilibrium distribution, even under continuous injection. In this scenario, no light is emitted under the injection of the electrons and holes.
In a direct-band semiconductor, electrons at the minimum of the conduction band have the same wavevector k (or momentum) as the electrons at the top of the valence band.	In contrast, in an indirect-band semiconductor, electrons at the minimum of the conduction band have a different wavevector k (or momentum) than the electrons at the top of the valence band.	In a metal, a band is filled by electrons until the Fermi level E_Fermi

click on image to enlarge it. Zayets 2024

Why does a direct-band semiconductor emit photons, while an indirect-band semiconductor emits phonons, but not photons?

A. This difference arises from the relationship between energy, momentum, and wave vector. For the same energy, a phonon has a much larger momentum and wave vector than a photon.

Momentum is inversely proportional to wave speed. The speed of sound (~300 m/s in air) is much slower than the speed of light (~3 × 10^8 m/s). Consequently, for a given energy, the momentum of a phonon is about a million times larger than that of a photon.

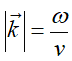
wher k is wave vector, ω is angular frequency and v is the speed of the wave particle.

In a direct-band semiconductor, the momentum (or wave vector) of an electron at the bottom of the conduction band is nearly the same as that of a hole at the top of the valence band. This means the transition between these states can be accompanied by a photon, which has a small momentum. Thus, photon emission is possible.

In an indirect-band semiconductor, however, the momentum of the electron at the bottom of the conduction band is very different from that of the hole at the top of the valence band. For a transition between these states, a wave particle with a much larger momentum, such as a phonon, is required to conserve momentum. As a result, the emission of photons is not possible, and phonon-assisted processes dominate.

Why does photon emission only occur for electron transitions from the top of the conduction band to the bottom of the valence band? Why can't the transition happen from a state in the middle of the conduction band or to a state in the middle of the valence band, where there is momentum matching for an indirect semiconductor??

A. The time an electron spends in a state in the middle of the conduction band is very short, far too brief for an electron transition to the valence band and photon emission to occur. For a photon to be emitted, the electron must remain in a quantum state long enough to allow the transition to the valence band, and this requires two conditions:

(condition 1): Electron Accumulation:

A sufficient number of electrons need to accumulate in the conduction band, leading to population inversion—where the number of electrons in a state of the conduction band exceeds those in a state of the valence band. This is essential for stimulated emission and photon generation.

(condition 2): Transition Time:

The electron transition from the conduction band to the valence band takes a finite amount of time, approximately equal to a quarter of the Rabi oscillation period. During this time, the electron must remain in its quantum state without being scattered.

A similar scenario applies to the valence band. States in the middle of the valence band remain unoccupied only for very short periods, making them unsuitable for electron transitions that result in photon emission. Thus, photon emission occurs only when electron transitions occur from the top of the conduction band to the bottom of the valence band.

Why are electron transitions within a band very fast, while transitions between bands are much slower?

A. Intra-band transitions (within a single band) are rapid because there are many closely spaced quantum states with small differences in energy and momentum. Frequent electron scattering events (e.g., due to phonons, impurities, or other electrons) easily move the electron toward the lowest available energy state. These transitions occur quickly as they do not require significant changes in momentum or energy, and conservation laws are easily satisfied.

Inter-band transitions (between different bands), on the other hand, take much longer due to two key reasons:

(reason 1): Large energy and momentum differences:

States in different bands typically have significant differences in both energy and momentum. Standard scattering processes cannot facilitate these transitions, as they would violate the conservation of energy and momentum. For an electron to transition between bands, an additional particle (such as a photon or phonon) is needed to balance the energy and momentum difference, which makes these transitions less frequent and slower.

(reason 2): Different spatial symmetries:

Transitions between states with different symmetries are less probable because the overlap of their wavefunctions is smaller. As a result, these transitions take longer due to the lower probability of such interactions.

Together, these factors make inter-band transitions significantly slower than intra-band transitions.

challenge with all-metal LED design

In semiconductor-based LEDs, the operation is not solely based on the different charges of electrons and holes but on differences in their spatial symmetry. Electrons in the conduction band typically have s-symmetry, while holes in the valence band have p-symmetry. This difference in symmetry reduces the probability of electron-hole interaction, allowing enough time for them to recombine radiatively and produce photons, while minimizing non-radiative recombination.

In contrast, in metals, both electrons and holes share the same symmetry, leading to very fast, non-radiative recombination. As a result, they combine too quickly to produce photons, making it difficult to generate light through radiative recombination.

(fact): Stimulated emission of light occurs only when the population of electrons in a higher energy state exceeds that of the lower energy state (population inversion).

In semiconductors, electrons and holes have different spatial symmetries, which slows their non-radiative recombination, helping to maintain a higher population of the upper energy level.

In contrast, in metals, electrons and holes share the same spatial symmetry, leading to rapid recombination. This quick recombination reduces the population of the higher energy state below that of the lower energy state, preventing the necessary population inversion for laser emission.

Possible solution of the challenge

(solution 1): Utilize a specific metal that has two energy bands with distinct symmetries at its Fermi level.

In this case, electrons will tunnel into the higher energy band and remain there for a relatively long time before relaxing into the lower energy band. The difference in spatial symmetries between the two bands slows down the recombination process, allowing for a sustained population of electrons at the higher energy level. This prolonged population could enhance the efficiency of photon emission by reducing non-radiative recombination.

(solution 2): Increase of the tunneling time

If hole-electron recombination occurs during tunneling, increasing the tunneling time can extend the duration that electrons remain in the higher energy state. This extended lifetime enhances the population of electrons at the higher energy level, potentially improving the efficiency of photon emission.

Operation of all- metal LED

LED made only from metals

Metal. Single Band	Metal. Double band. InDirect	Metal. Double band. Direct
no light emission	no light emission	there is light emission

In the case of a single band metal, the high-energy electrons rapidly move down, and the low-energy holes quickly move up. These fast electron movements ensure that the electrons and holes maintain a near-equilibrium distribution, even under continuous injection. The injected electrons quickly filled the injected holes. Except for some heating, the electron and hole injection do not lead to any effect. No light is emitted under the injection of the electrons and holes.	The case where a metal has a second band above the Fermi energy. Under a sufficiently high applied voltage, electrons are injected into this second band while holes are injected into the first band. The injected electrons quickly move down to the bottom of the second band, and the holes rapidly move up along the first band toward the Fermi level. In the shown case, the momentum of the electrons at the bottom of the second band and the electrons at the Fermi level of the first band are different. As a result, a direct electron transition from the second band to the first band would require the involvement of a phonon, which is a particle with large momentum. Because the photon has relatively small momentum compared to a phonon, light emission does not occur in this process. Instead, the transition is governed by phonon participation, which does not produce light.Thus, under electron and hole injection, no light is emitted due to the momentum mismatch and the requirement for phonon involvement.	This case is similar to the one shown at the left, but with a lower Fermi energy. In this scenario, the Fermi energy is adjusted so that the momentum of the electrons in the first band at the Fermi level matches the momentum of the electrons at the bottom of the second band. When an electron transitions from the second band to the first band, it emits a photon. In this situation, light is emitted when electrons and holes are injected from the metals on sides 1 and 2. This setup allows for the possibility of laser emission in a structure composed entirely of metals, without the need for semiconductors.This illustrates a scenario where laser emission could be realized in an all-metal system.

When a voltage is applied across three metal regions, the electron energy becomes higher in the metal on side 1 and lower in the metal on side 2. As a result,high-energy electrons are injected from the metal on side 1, while low- energy holes are injected from the metal on side 2. Due to very fast electron scattering within the bands, the high-energy electrons rapidly move down, and the low-energy holes quickly move up.

click on image to enlarge it. Zayets 2024

Tackling the Issue of Strong Light Absorption in Metals

When discussing an "all-metal LED," one significant challenge that arises is the strong light absorption inherent to metals. Metals are well-known as some of the strongest absorbers of light. This raises a critical question:What is the benefit of generating laser light inside a metal if that light is immediately absorbed? At first glance, it might seem illogical to fabricate an all-metal LED if the emitted light cannot effectively escape the metal.

What is the benefit of generating laser light inside a metal if that light is immediately absorbed?

A. The all-metal LED can be optimized to ensure that the emitted light is minimally (nearly not) absorbed by the metal.

(fact): There are many optical devices made of a metal and still having a low optical absorption.

(Example 1): conventional mirror. Even though the reflective coatings in mirrors are made from metals like aluminum or silver, the mirror absorbs nearly no light and reflects nearly all of it.

(Example 2): plasmonic optical devices. In plasmonic devices, the overall loss due to light absorption is much smaller than you might expect. In fact, with proper design, the losses in a plasmonic device can be comparable to those in conventional, metal-free optical devices. Please see the technology of low-loss plasmonic devices, which I have developed for Si Photonics here.

Two strategies to significantly minimize light absorption in metals:

By employing these techniques, the light absorption in metals can be effectively reduced and, therefore, managed. As a result, the challenge of light absorption in metals does not present a significant obstacle to the successful development and operation of an all-metal LED.

(strategy 1): Surface Plasmons

Unlike conventional light waves that propagate through the bulk of a material, surface plasmons are confined to the surface of a metal. As a result, the electromagnetic field of the plasmon resides mostly in the adjacent dielectric material, with only a small fraction penetrating into the metal.. This limited penetration significantly reduces the absorption within the metal, thereby minimizing plasmonic losses.

(strategy 2): Blocking free-electron absorption

The free-electron absorption, which is the primary source of light loss in metals. This type of absorption occurs when the conduction electrons oscillate in response to the electric field of light. By designing structures composed of ultrathin metal layers—each less than 1 nanometer thick—separated by dielectric materials, electron movement perpendicular to the plane of the layers is effectively restricted. This configuration significantly suppresses free-electron absorption when light propagates along the structure and the electric field is oriented perpendicular to the plane.

Blocking free-electron absorption

Mechanism to block light absorption by a metal

By employing these techniques, the light absorption in metals can be effectively reduced

conventional metal		free-electron absorption is blocked
high optical loss		low optical loss

(structure): light propagates through a thick metal (Fe) (shown in green)		(structure)a thin metal layer (~0.2-0.6 nm) separated by a thin non-conductive material (MgO) (shown in blue). Light propagates along interfaces with polarization directed perpendicular to the interfaces (TM polarization).
(Reason for Light Absorption): Light absorption occurs because the oscillating electric field of the light forces the conduction electrons in the metal to move. As these electrons move, they lose energy due to the electrical resistance of the metal, leading to light absorption.		(Reason for the Absence of Light Absorption): In structures where the thickness of the metal layers is smaller than the electron mean free path, the electrons are confined and cannot move along the thickness of the metal. Although the oscillating electric field of light still exerts a force on the electrons, their motion is restricted in the direction of the field. As a result, energy loss through electron movement is suppressed, and light absorption is effectively eliminated.

The oscillating electrical field (brown arrow) of TM- polarized light (blue arrow) forces a conduction electron (blue ball) to move perpendicularly to the interface.

click on image to enlarge it.

Zayets 2024.12

(note) This same mechanism is utilized in the fabrication of thin-film light polarizers.

How thin should the metal layer be to block free-electron absorption?

Answer: The required thickness depends on the electron mean free path of the material. To block free-electron absorption, the metal layer thickness must be at least smaller than the electron mean free path.

In semiconductors, where the electron mean free path is relatively long, electron confinement occurs at a layer thickness of about 10–15 nm.

In metals, however, the electron mean free path is much shorter, so the metal layer must be extremely thin—typically less than 1 nm, with a typical range of about 0.4–0.6 nm.

(device 2): Field-Effect Transistor (FET) made of only metals

(conventional semiconductor FET): In a semiconductor-based FET, two n-type regions are separated by a p-type region. Without a gate voltage, no current flows between the source and drain because the p-n junction is reverse-biased. When a gate voltage is applied, the Fermi level in the p-type region shifts, converting a small area under the gate from p-type to n-type, which opens the channel and allows current to flow.

(all-metal FET): There is no feasible design

Why is it not feasible to make a Field-Effect Transistor (FET) of only metals without usage of a semiconductor?

A. The essential principle behind the operation of an FET is the ability of the semiconductor to switch between a conductive and non-conductive state.

However, it is not feasible to create an FET using only metals. Metals are always conductive, and even though applying a gate voltage can shift the Fermi level, the metal will remain highly conductive. As a result, the required switching mechanism between conductive and non-conductive states cannot be achieved solely with metals.

(device 3): Bipolar Transistor made of only metals

(conventional semiconductor Bipolar Transistor): In a semiconductor-based bipolar transistor, two n-type regions are separated by a very thin p-type region. This thin p-region allows electrons to diffuse between the two n-type regions. The voltage applied between the p-type region and one of the n-regions modulates the depletion width, effectively changing the width of the p-region. This, in turn, alters the diffusion time of the electrons through the p-region, thereby modulating their transmission and controlling the emitter-collector current.

(all-metal Bipolar Transistor): In the design of an all-metal bipolar transistor design the three metals would serve as the emitter, base, and collector, with oxide layers inserted between each region to act as tunnel barriers. The current from emitter to collector flows via tunneling, and the base voltage modifies the height of the tunnel barrier, thereby modulating the emitter-collector current.

Bipolar Transistor made of only metals

conventional semiconductor Bipolar Transistor	Can an Bipolar Transistor be made entirely from metals?	all-metal Bipolar Transistor

When a voltage is applied between the emitter and collector, electrons diffuse from the n-type emitter to the n-type collector through the thin p-type base. The current depends on the effective thickness of the p-type base. The voltage applied to the base creates a depletion layer between the n- and p-type regions, which reduces the effective thickness of the p-type region. As the p-type region's thickness decreases, the probability of hole-electron recombination in this region also decreases, leading to an increase in the current flowing from collector to emitter. Thus, the base voltage effectively modulates the emitter-collector current in the bipolar transistor.		When a voltage is applied between the emitter and collector in an all-metal bipolar transistor, a tunneling current flows first from the emitter to the base, then tunneling current flows from the base to the collector. The base voltage modulates the heights of both the emitter-base and base-collector tunnel junctions, thereby adjusting the tunneling current through each junction. As a result, the voltage applied to the base controls the emitter-collector current, enabling modulation of current flow in the all-metal bipolar transistor.

click on image to enlarge it. Zayets 2024

challenge with this all-metal Bipolar Transistor design.

One key feature of semiconductor-based transistors is the relatively long interaction time between electrons and holes. This extended interaction allows electrons to travel significant distances within the p-type region, meaning even a small change in the effective thickness of the p-region can greatly influence electron transmission.

For this reason, creating a highly efficient bipolar transistor using only metals is quite challenging.

Operation of semiconductor bipolar transistor

switched ON

The voltage V_BC applied between the gate and collector widens the depletion region in the p-type base, effectively narrowing the width of the p-type region. This reduction in width shortens the diffusion time for electrons traveling through the base, thereby decreasing the probability of electron-hole recombination. As a result, the emitter-to-collector current increases, switching on the bipolar transistor.

switched OFF

In the absence of voltage V_BC between the gate and collector, the depletion region becomes narrower, causing the effective width of the p-type base to increase. As a result, the diffusion time for electrons traveling through the base is longer, which increases the probability of electron-hole recombination. This higher recombination rate reduces the emitter-to-collector current, effectively turning off the bipolar transistor.

(key operational principle of semiconductor bipolar transistor):

The base voltage controls the time required for electrons to pass through the effective p-type region. By modulating this transit time, the base voltage alters the rate of electron-hole recombination and, consequently, the number of electrons that reach the collector. This modulation of electron flow creates the current gain in a semiconductor bipolar transistor.

click on image to enlarge it

(device 2): Field-Effect Transistor (FET) made of only metals

() Why is it not feasible to make a Field-Effect Transistor (FET) of only metals without usage of a semiconductor?

(device 3): Bipolar Transistor made of only metals

() challenge with this all-metal Bipolar Transistor design

() Operation of semiconductor bipolar transistor

() Operation of all- metal bipolar transistor

Operation of all- metal bipolar transistor

switched ON

The

switched OFF

In

(key operational principle of metal bipolar transistor):

The base voltage controls how long electrons, after tunneling from the emitter to the base, remain at a higher energy level before relaxing to a lower equilibrium state. Since the probability of electrons tunneling from the base to the collector is significantly higher from the higher energy level than from the lower energy level, the base voltage effectively modulates the current flowing from the emitter to the collector. This modulation results in the current gain characteristic of a metal bipolar transistor.

Zayets 2024, click on image to enlarge it

(approach 2): All- Metal Devices Adapting Entirely New Operational Principles:

This approach explores novel concepts and mechanisms that have not been utilized in semiconductor-based devices. These new principles would be specifically designed to leverage the unique properties of metals, potentially leading to innovative types of electronic and data-processing devices that operate in fundamentally different ways from their semiconductor counterparts. One such unique property of metals is ferromagnetism, along with the associated phenomenon of magnetoresistance.

Ferromagnetic metals exhibit spontaneous magnetic ordering, which can be harnessed to create devices that rely on the manipulation of magnetic domains rather than traditional charge-based mechanisms. Additionally, magnetoresistance—where the electrical resistance of a material changes with respect to the magnetization direction- may be used as a current switching mechanism. These properties could be key in developing all-metal devices that outperform or complement existing semiconductor technologies.

Magnetoresistance as switching effect in all- metal transistor

Design 1 of proposed all-metal transistor.


Without gate voltage, magnetization of nanowire is in-plane. Since magnetization of all domains in one direction, nanowire resistance is low and the transistor is in "ON" state.	Under a gate voltage, the magnetization under gate turn to be perpendicular. The magnetization in gap remains in-plane. Due to different magnetization directions of neighbor domains, nanowire resistance increases and the transistor is changed to "OFF"state.

Ferromagnetic metal with in-plane equilibrium magnetization. click on image to enlarge it

Design of proposed all-metal transistor

Design 1. Ferromagnetic metal with in-plane equilibrium magnetization

gate voltage: DC or pulse

The magnetization direction under the gate is changed by the VCMA effect.

Design 2. Ferromagnetic metal with perpendicular -to -plane equilibrium magnetization

Design 2 of proposed all-metal transistor.


Without gate voltage, magnetization of nanowire is perpendicular -to -plane. Since magnetization of all domains in one direction, nanowire resistance is low and the transistor is in "ON" state.	Under a pulse of gate voltage, the magnetization under gate is reversed. The magnetization in gap remains the same. Due to different magnetization directions of neighbor domains, nanowire resistance increases and the transistor is changed to "OFF"state.

Ferromagnetic metal with in-plane equilibrium magnetization. click on image to enlarge it

gate voltage: pulse only

(experiment): Observed High switching ratio in FeBTb nanowire with periodically modulated PMA

High MR in FeBTb nanowire with periodically Pt electrode

Measured MR curve	structure of FeBTb nanowire with periodically modulated PMA	Resistance of nanowire is changed by the magnetic field

Magneto-resistance of FeBTb(3 nm): Pt(3 nm) 400-nm-wide wire with periodically modulated PMA. room temperature. Measurement date: July 2015.	Pt was etched into 80-nm stripes with 120-nm gaps. Without magnetic field the resistance of nanowire is high.	Under magnetic field the resistance decreases

Detailed experimental data see below. click on image to enlarge it

Pt induces perpendicular magnetic anisotropy (PMA) in FeBTb.

Additionally, there is a volume-type PMA in FeBTb. As a result, a thicker FeBTb nanowire has a larger PMA than a thinner nanowire.

Under Pt gate the PMA is larger than in the gap between electrodes, because interface PMA at Pt/FeBTb interface and because in this region the FeBTb is thicker.

To see experimental details of high MR measurements in FeBTb/Pt nanowire, click here to expand

Top SEM image	Measured MR curve	Hall rotation angle

(left) FeBTb nanowire with Pt periodical gate is directed from bottom to top. The Hall probe is directed from left to right. For this measurement the hall angle represents the average Hall angle in region under gate and in the gap between gate electrodes. magnetic field is applied perpendicularly to the sample. Measurement date: July 2015. click on image to enlarge it

FeBTb is a compensated ferromagnetic. Magnetic moments of Fe and Tb are coupled antiferromagnetically.

the FeBTb with small Tb concentrations was studied. As a result, the total magnetization of Fe is larger than the magnetization of Tb atoms

The PMA in the FeBTb film is the volume-type. The PMA in the FeBTb film increases when thickness increases. The equilibrium magnetization of used FeBTb (3 nm) is in-plane.

suggested magnetization directions under a different perpendicular magnetic field

no magnetic field: H=0 kG

Magnetization is in-plane. The magnetization of Fe and Tb are anti parallel each other. Magnetization of Fe in regions under gate and between gates are anti parallel each other as well.

magnetic field: from 0 to 5 kG

Both the magnetic moments of Tb and Fe turn toward the magnetic field. The angle between the magnetic moments becomes smaller than 180 degrees.

magnetic field: from 5 to 7.5 kG

Hall rotation angle & suggested magnetization directions in regions under gate and between gate

Red arrow shows suggested magnetization of Fe. Blue arrow shows suggested magnetization of Tb. click on image to enlarge it

Anti ferromagnetic interaction between Fe and Tb becomes stronger than the dipole interaction with external magnetic field. The magnetic moments of Tb and Fe turn to be anti parallel each other again. In both regions under and between gate the magnetic moments of Fe become parallel.

magnetic field: above 7.5 kG

The magnetic moments of Fe become anti parallel in regions under Pt gate and between gates.

(unique nano measurements):Measuring Magnetization Dynamics Individually Under a Nano Gate and in a Neighboring Nano Gap

FeBTb nanowire with periodic gate and two Hall probes. Top SEM view

Whole structure	Hall probe connected under gate	Hall probe connected in gap between gate electrodes	FeBTb nanowire with Pt periodic electrode.

Nanowire with periodical gate are directed from bottom to top. Wires, which directed from left to right, are Hall probes. Bottom probe is connected under gate. Top probe is connected in gap.	These Hall electrodes are aligned to measure the magnetization under gate	These Hall electrodes are aligned to measure the magnetization in gap between gate electrodes	Periodic Pt electrodes on a ferromagnetic nanowire, which induces the periodical PMA in the wire. The front Hall probe contacts the region under the Pt electrode. The back Hall probe contacts the region in the gap between Pt electrode.

Top SEM view. click on image to enlarge it

In order to optimize the transistor, it is important to measure the magnetization independently and simultaneously in regions under the electrode and in gap between electrodes. It clarifies whether

(1) magnetization is magnetically decoupled in these regions

(2) magnetization direction in each region

The size of tip of Hall bar should be sufficiently narrow! Now I am able to make the tip as narrow as 40-50 nm.

The alignment of tip should be very precise! Now I am able to make the alignment between Hall probe and the periodical electrode with 10 nm precision.

(measurement):Coupling & decoupling of magnetization in regions under gate and in gap between gates

The exchange interaction between regions under gate and in gap between gates forces forces

Decoupling of magnetization in regions under gate and in gap between gates

Fully decoupled	Partially decoupled	Not- decoupled

Both the coercive field and the Hall angle are different in the gap and the gap regions	Only the Hall angle are different	Both the coercive field and the Hall angle are exactly the same in the gap and the gap regions

click on image to enlarge it

Gate with periodical change of polarity

In this structure, a gate voltage of opposite polarities is applied to neighbor gate electrode. The Hall probe (from left and from right) is precisely aligned to measure the magnetization direction at each gate electrode. Top SEM view.

click on image to enlarge it

Gate with periodical change of polarity

In this structure, a gate voltage of opposite polarities is applied to neighbor gate electrode. As a result, under one gate electrode the PMA of the nanowire increases and under neighbor electrode the PMA decreases. That enhances the formation the gate-voltage-induced domain structure in the nanowire.

Pinning of domain wall & Pinning of magnetization in gap between gate electrodes

Pinning of domain wall & magnetization in gap between Pt gate electrodes	FeBTb nanowire with Pt periodic electrode.	FeBTb nanowire with Pt periodic electrode.

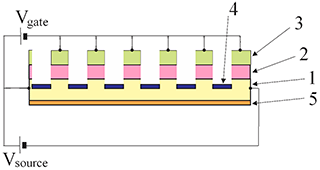Basic structure of all-metal transistor. (1)ferromagnetic nanowire; (2) gate oxide (3) gate electrode (4) material to enhance interfacial PMA in the gap; (5) substrate. click on image to enlarge it	Periodic Pt electrodes on a ferromagnetic nanowire, which induces the periodical PMA in the wire. The front Hall probe contacts the region under the Pt electrode. The back Hall probe contacts the region in the gap between Pt electrode. The region in the gap is deeply etched into the nanowire in order to pin a domain wall at boundary between these regions. click on image to enlarge it	The same as left picture, but SiO2 layer is not shown. click on image to enlarge it

The pinning of domain wall and pinning of magnetization in gap between gate electrodes are critically important for the operation of the transistor.

A different thickness of nanowire is used to pin firmly the domain at the boundary between the gate electrode and the gap.

The material with a large interfacial PMA is deposited in the gap between gate electrode in order to pin the magnetization in this region

Effect of accumulated magneto-resistance

In fact, the magneto-resistance (MR) is not accumulated effect. The total magneto-resistance of two or more MR elements, which are connected either parallel or in series, is smaller or equal to the magneto-resistance of each MR element.

In contrast, in a nanowire with magnetic domains the magneto-resistance may be accumulated

Magneto-resistance is not accumulated effect

in parallel	in series

In either case, the total MR equals to the MR of each element! click on image to enlarge it

Example 1: Two MR elements are connected in series

In this case total resistance can be calculated as

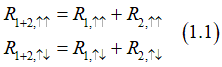
where are resistance of 1st and 2d elements of their two electrodes are parallel. are resistance of 1st and 2d elements of their two electrodes are anti parallel.

The total magneto-resistance can be calculated as

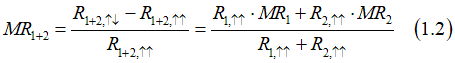
in the case when two MR elements have an equal magneto-resistance , the total MR is the same as MR of each element

Example 2: Two MR elements are connected in parallel

In this case total resistance can be calculated as

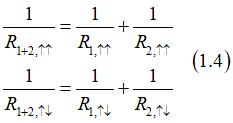
in the case when MR and resistance are equal

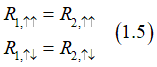
The total resistance can be calculated from Eq.(1.4) as

From Eq. (1.6), the total MR is calculated as

the total MR is the same as MR of each element

Accumulation of magneto-resistance in a nanowire with magnetic domains

Accumulation of magneto-resistance in a ferromagnetic nanowire with domain walls

3 domain walls

6 domain walls

9 domain walls

12 domain walls

MR increases when number of domain walls increases and domain size decreases!!

Click on image to enlarge it

The magneto-resistance of a ferromagnetic nanowire with domain walls is calculated as

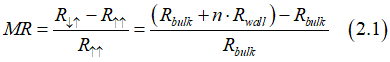
where R_bulk is the bulk resistance of the nanowire without any domains, R_wall is the resistance of one domain wall and n is number of domain walls.

From Eq(2.1), is MR is calculated as

The magneto-resistance (MR)increases when number of domain walls n increases and domain size decreases!!

How large is the resistance R_wall of one domain wall?

1. The smaller domain size , the larger MR !!

2. The shorter domain wall,.the large MR!!

Click on image to enlarge it

The change of resistance on nanowire, which is made of Fe or Co, is about 0.1-0.01% (70 K) ( Kent et al, JCMCP (2001)) . Usually, it is about the same magnitude as the resistivity change due to the Anisotropic magnetoresistance (AMR). I have never observed the domain wall resistance in Fe, FeB, Co in my experiments at room temperature. Even though I have fabricated a nanowire made of these materials with 50 nm long domains, which was checked by Hall measurements (See here). In contrast, a nanowire made of a compensated ferromagnet (like FeBTb) always shows a substantial domain wall resistance and a substantial AMR. I am not sure weather the domain wall resistance and the AMR are related.

The resistance of one domain was measured in 60-nm-wide FePd nanowire at 17 K. It was about 0.01 Ohm, when total resistance of nanowire was 3 Ohm (Danneau et al, PRL 2002)

How to increase the domain-wall-induces magneto-resistance?

method 1: Reduce size of a domain

The smaller domain size , the larger MR ! See fig. above. The periodically-modulated PMA is the method to obtain the shortest domain.

method 2: Make a shorter domain wall

The magnetization direction is opposite for neighbor domains. The spin direction of spin-polarized conduction electrons is along the magnetization in the bulk of the domain. However, in the region of the domain wall the spin-polarization becomes zero (See here). The magneto-resistance may occurs when electron current is passing through the regions of different spin polarization of the conduction electrons. The steeper the change of spin polarization is, the larger the MR is. Therefore, the domain structure with the shortest domain wall is required in order to obtain a substantial MR.

Example: (1) in Fe:MgO:Fe MTJ device, the spin polarization of the conduction electrons changes sharply from one Fe electrode to another Fe electrode. As a result, the MR is very high ~100 %; (2) in Co:Cu:Co p-GMR device , the spin polarization changes very gradually from one Co electrode to another Co electrode. As a result, the MR is moderate ~0.1 %; It should be noted that other material parameters influence the MR, but tendency is clear.

method 3. Use a compensated ferromagnetic material or an antiferromagnetic material as a material of nanowire

Up to now (Aug.2018) I have never detected any domain wall resistance in a nanowire made of FeB or Co or Fe, which were measured at room temperature. However, I often detect the domain wall resistance in the compensated ferromagnetic FeBTb.

method 4 Use a material with a low conductivity. Use a "bad" conductor

All spin-dependent features more manifest themselves in a metal with a lower conductivity (in a "bad" conductor). The reason for this is that the nature of electrical current is very different from that in a "good" conductor. (See here). The magneto-resistance only may occur in the "bad" conductor, but it can not be any magneto-resistance in the "good" conductor (See here).

Why the most of reports on the resistance of a domain wall is done at low temperature?

There are two reasons for that:

reason 1: The spin polarization of the conduction electrons becomes larger due reduction of the spin relaxation time (See here).

reason 2: The gradient of the spin polarization in the region of the domain wall becomes sharper.

Main Challenges

Main challenge is to obtain a sufficient domain wall resistance.

It can be only achieved in a metal with a high resistivity. There is a fundamental reason for that (See here)

Convolutional Neural Network

The proposed design may be used as a memory element of a Neural Network.

Many neuromorphic specific circuits can be represented as neural gates performing the operation of a “dot product” of vectors of analog inputs and stored weights (synapses), followed by a non-linear threshold function (a neuron).

A logic element has only two states: 0 and 1. For neuron computing, a memory element with a larger number of states is required. In the proposed design, the resistance of the device can be increased by given amount when the gate voltage is applied only to some (not to all) electrodes and only some of domains are reversed.

I am strongly against a fake and "highlight" research

Dr. Vadym Zayets

v.zayets(at)gmail.com

more Chapters on this topic:

more Chapters on this topic:

Spin and Charge Transport

Abstract:

Content

click on the chapter for the shortcut

() Why does a direct-band semiconductor emit photons, while an indirect-band semiconductor emits phonons, but not photons?

() Why is it not feasible to make a Field-Effect Transistor (FET) of only metals without usage of a semiconductor?

Patent: "All-metal transistor and its operational method" , “全金属型トランジスタとその方法” V. Zayets,T. Nozaki, A.Fukushima, S. Yuasa, Patent application 2017-226503, H29/06/06 ( figures; in Japanese; in English)

What are the benefits of avoiding semiconductor materials in the fabrication of transistors or electrical switches?

Terminator 2: science-fiction movie

Main advantage: Ideal for dense 3D integration:

Why could an all-metal transistor be superior to a semiconductor transistor?:

electronic and data - processing devices made of only metals: 2 approach

without usage of semiconductors

Two potential approaches for fabricating electronic and data-processing devices using only metals:

All- Metal Devices Adapting Similar Operational Principles Used in Semiconductor Devices

(device 1): Laser Emitting Diode (LED) made of only metals

conventional semiconductor LED

Can an LED be made entirely from metals?

all-metal LED

Operation of semiconductor LED. Direct Gap vs. Indirect Gap Semiconductors

Direct Band semiconductor (e.g. GaAs)

InDirect Band semiconductor (e.g. Si)

Metal (e.g. Au). Single band

challenge with all-metal LED design

Possible solution of the challenge

Operation of all- metal LED

Metal. Single Band

Metal. Double band. InDirect

Metal. Double band. Direct

no light emission

no light emission

there is light emission

Tackling the Issue of Strong Light Absorption in Metals

What is the benefit of generating laser light inside a metal if that light is immediately absorbed?

Two strategies to significantly minimize light absorption in metals:

By employing these techniques, the light absorption in metals can be effectively reduced and, therefore, managed. As a result, the challenge of light absorption in metals does not present a significant obstacle to the successful development and operation of an all-metal LED.

Mechanism to block light absorption by a metal

conventional metal

free-electron absorption is blocked

high optical loss