Dr. Vadym Zayets
v.zayets(at)gmail.com
My Research and Inventions
click here to see all content |
Dr. Vadym Zayetsv.zayets(at)gmail.com |
|
|
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
|
Magneto-optical effect
Spin and Charge TransportAbstract:The origin of the Magneto-Optical (MO) effect is the Zeeman spliting of energy levels in a magnetic field. The non-zero electron orbital moment might significantly influence the magneto-optical effect. The spin-orbit interaction might significantly enhance the magneto-optical response.The magneto-optical response significantly depends on the degree of quenching of the orbital moment of the delocalized electrons in the material. The spin accumulation may also cause the magneto-optical response.
|
 |
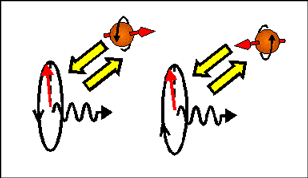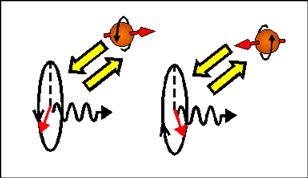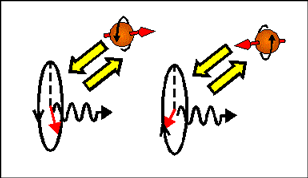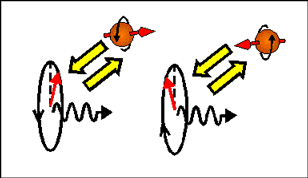The case when light interacts with electrons of one spin. It is only the case when the light polarization rotates around axis parallel to the spin. As example, light with the polarization rotating in clockwise direction interacts only with spin-left electrons and light with the polarization rotating in anticlockwise direction interacts only with spin-right electrons.. |
The right- circularly polarized light
(polarization rotates in clockwise direction) transfer spin orbital moment 
, where is 
the reduced Planck constant.
The spin orbital moment is directed opposite to the light propagation direction.
The left- circularly polarized light
(polarization rotates in counterclockwise direction) transfer spin orbital moment 
,
The spin orbital moment is directed along the light propagation direction.
In magnetic field a magnetic moment aligns itself along the direction of the applied magnetic field. Therefore, electrons, which magnetization is along magnetic field have a smaller energy than electrons, which magnetization is opposite to the magnetic field. Since the magnetic moment of an electron is directed opposite to the electron spin and the electron orbital moment, an electron with spin directed along the magnetic field has a larger energy than an electron with opposite spin direction.
Origin of the Magneto-Optical effect is the Zeeman effect |
|
| In a magnetic-field, electrons, which spin are parallel and antiparallel to the magnetic field, have different energy (Zeeman effect). Left- and right- circular polarized light induces transitions to different spin-subbands. Therefore, left- and right circular polarized light experiences different refractive index and absorption. The arrows shows direction of electron magnetic moment. |
Q. The g-factor of elctron spin is -2 and the orbital moment is -1. By measuring the Zeeman spliting is it possible to determine whether the orbital moment of delocalized electrons in a solid is quenched or not.
A. No. In a solid the Zeeman spliting is considered to be proportional to the electron spin, but not the orbital moment or the total moment. In case if the orbital moment could contribute to the Zeeman spliting the electron orbit in a solid should be able to precess (see here), which is impossible even in a case of a weak quenching.
Q. Why the g-factor of delocalized electrons is different from -2.
A. Mainly because of the spin-orbit interaction. Because of the spin-orbit interaction the effective magnetic field, which a delocalized electron experiences, is different from the externally applied magnetic field. For example, if 1 kG of magnetic field is applied, the effective magnetic field, which electron experience and which causes the Zeeman spliting, might be 3 kG.
Q. Where the effective field of the spin-orbit interaction is originated from?
A. From electrical field of a nucleus. Because of the reletivistic nature of the electrical and magnetic fields, when electron moves in an electric field, it experiences a magnetic field. Since in a solid an delocalized electron can be very close to the nucleus, the effective magnetic field can be strong.
Q. Is the effective magnetic field of the spin-orbit interaction is a real magnetic field?
Because circularly polarized light interacts only with one of two electrons of "full" state, it split the "full" state without spin into two "spin" states with opposite spin direction
It is imaginary case. In real material the orbital moment is not "fully" quenched or "fully" unquenched
Absorption of left circularly polarized light by a direct-band semiconductor |
||
|
||
Fig. 10. When left- circularly polarized light is absorbed, its spin orbital moment of +1 transforms to the excited electron. The electrons with spin S= -1/2 of the light-hole (lh) and heavy hole (hh) bands are excited to an empty state with spin S= +1/2 of the conduction band (ee). Since transformed spin orbital moment is directed along the light propagation direction and the direction of the magnetic field, only electrons, which spin is directed opposite to the magnetic field (spin-left), are excited. Light creates spin polarization in direction of the magnetic field for electrons of both the conduction and the valence bands. |
In this case the magnetic moment of circularly -polarized light is transformed into accumulation of electron spin, but not into accumulation of the orbital moment.
In the case of a semi-isolating semiconductor, the Fermi level is near the middle of the band gap. There are no electrons in the conduction band. In the conduction band all states are "empty" states without any spin. All states in the valence bands are occupied. All states in valence bands are the "full" states without spin as well. Even though each "full" state is occupied by two electrons of opposite spins, each electron is not distinguished, the electron spins do not have defined direction and the "full" state can be considered as one particle without spin. In a magnetic field the energy of the "full" state remains unchanged, because the "full" state has no spin. Similar to a "full" state, an "empty" state does not interact with the magnetic field.
When the left circularly -polarized light starts to interact with one electron of the "full" state, each electron of the "full" state becomes distinguished. Therefore, they starts to behave not as as one electron with no defined spin, but as two separated electrons with spin directions along and opposite to the light propagation direction. The electron with spin along magnetic field (magnetic moment is opposite to the magnetic field) has a higher energy than the electron with spin opposite to the magnetic field.
The energy, at which left-circularly-polarized light is absorbed due to the electron transition from the heavy-hole (hh) band to the conduction band (ee), is
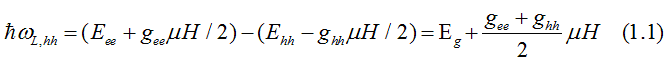
The energy, at which left-circularly-polarized light is absorbed due to the electron transition from the light-hole (hh) band to the conduction band (ee), is
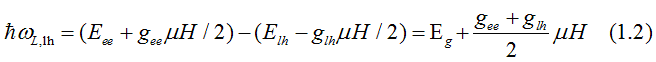
Q. Why left-circularly-polarized light is absorbed only by a spin-left electron, but not by spin-right electron? Is any special relation between left-circularly-polarized light and spin-left electrons?
A. No, there is no any special relation. The left-circularly polarized light has spin orbital moment +1, which transfer to an excited electron. When the spin-left electron (S=-1/2) is excited, its spin turns right (S=-1/2+1=1/2). The spin-right electrons (S=+1/2) also could be excited in the case if an empty electron state with spin=1/2+1=3/2 were available. Since there is no such state, the spin-right is not excite and it does not interact with left-circularly polarized light.
Absorption of right circularly polarized light by a direct-band semiconductor |
||
|
||
Fig.11. When right- circularly polarized light is absorbed, its spin orbital moment of -1 transforms to the excited electron. The electrons with spin S= +1/2 of the light-hole (lh) and heavy hole (hh) bands are excited to an empty state with spin S= -1/2 of the conduction band (ee). Since transformed spin orbital moment is directed opposite to the light propagation direction and the direction of the magnetic field, only electrons, which spin is directed along to the magnetic field (spin-right), are excited. Light creates spin polarization in direction of the magnetic field for electrons of both the conduction and the valence bands. |
The energy, at which right-circularly-polarized light is absorbed due to the electron transition from the heavy-hole (hh) band to the conduction band (ee), is
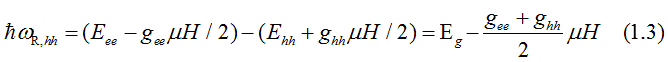
The energy, at which right-circularly-polarized light is absorbed due to the electron transition from the light-hole (hh) band to the conduction band (ee), is
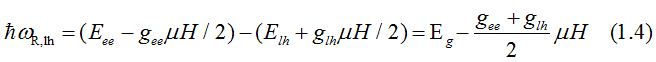
The absorption energy of the left-circularly polarized light is larger than the right -circularly polarized light. The difference of the absorption energies between the left and right circularly polarized light in the approximation of fully- quenched orbital moment is
Because of this difference the absorption energies, the left- and right- circularly- polarized light has different absorption coefficient and refractive index. It is the origin of the magneto-optical effect in a solid.
Note: in the case when g-factor for the light and heavy holes is the same, the MO transition energies for the heavy and light holes are the same. They are the same only in the case the approximation of fully- quenched orbital moment.
Q. Why right circularly-polarized light is absorbed only by a spin-right electron, but not by spin-right electron? Is any special relation between right-circularly-polarized light and spin-right electrons?
A. No, there is no any special relation. The right-circularly polarized light has spin orbital moment -1, which transfer to an excited electron. When the spin-right electron (S=+1/2) is excited, its spin turns left (S=+1/2-1=-1/2). The spin-left electrons (S=-1/2) also could be excited in the case if an empty electron state with spin=-1/2-1=-3/2 were available. Since there is no such state, the spin-left is not excite and it does not interact with right-circularly polarized light.
It is imaginary case. It assumes that delocalized electrons in solid behave identically as electrons on orbit of an atom of gas (like hydrogen gas)
In real material the orbital moment is not "fully" quenched or "fully" unquenched
Absorption of left circularly polarized light by a direct-band semiconductor. Orbital moment is unquenched |
||
|
||
Fig. 12. When left - circularly polarized light is absorbed, its spin orbital moment of +1 transforms to the excited electron. The electrons of heavy-hole band (hh) with total moment j= -3/2 are excited to the conduction band (ee) to an empty state with j= -1/2. The electrons of light hole band (hh) with total moment j= -1/2 are excited to the conduction band (ee) to an empty state with j= +1/2. In both cases the electron spin does not change direction. Only the orbital moment changes. The red, brown and violet arrows shows directions of the spin, the orbital moment and the total moment correspondingly. Light creates polarization of the total orbital moments (not spins) in the valence bands, which is directed along to the applied magnetic field. In the conduction band, the electron gas is spin-polarized only when the probabilities of electrons from hh and lh bands are different. |
The energy, at which left-circularly-polarized light is absorbed due to the electron transition from the heavy-hole (hh) band to the conduction band (ee), is
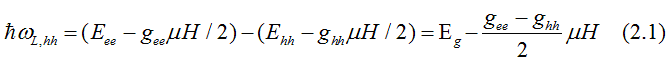
The energy, at which left-circularly-polarized light is absorbed due to the electron transition from the light-hole (hh) band to the conduction band (ee), is
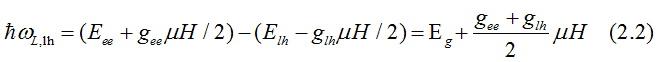
Absorption of right circularly polarized light by a direct-band semiconductor. Orbital moment is unquenched |
||
|
||
Fig.13. When right - circularly polarized light is absorbed, its spin orbital moment of -1 transforms to the excited electron. The electrons of heavy-hole band (hh) with total moment j= +3/2 are excited to the conduction band (ee) to an empty state with j= +1/2. The electrons of light hole band (hh) with total moment j= +1/2 are excited to the conduction band (ee) to an empty state with j= -1/2. In both cases the electron spin does not change direction. Only the orbital moment changes. The red, brown and violet arrows shows directions of the spin, the orbital moment and the total moment correspondingly. Light creates polarization of the total orbital moments (not spins) in the valence bands, which is directed opposite to the applied magnetic field. In the conduction band, the electron gas is spin-polarized only when the probabilities of electrons from hh and lh bands are different. |
The energy, at which right -circularly-polarized light is absorbed due to the electron transition from the heavy-hole (hh) band to the conduction band (ee), is
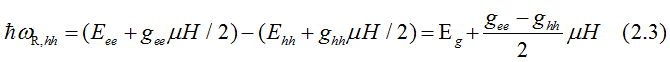
The energy, at which right -circularly-polarized light is absorbed due to the electron transition from the light-hole (hh) band to the conduction band (ee), is
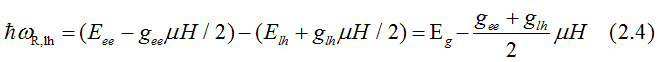
For the electrons of the light-hole band the absorption energy of the left-circularly polarized light is larger than the right -circularly polarized light. For the electrons of the heavy-hole band the absorption energy of the left-circularly polarized light can be either larger or smaller than the absorption energy the right -circularly polarized light depending on the ratio of the g-factors between the electron and heavy-hole bands. The difference of the absorption energies between the left and right circularly polarized light in the approximation of fully-unquenched orbital moment is
According to the Luttinger–Kohn model, the probability to excite an electron by light from the heavy-hole band is 3 times higher than from the light-hole band!!
Q. The 3-time difference of absorption probabilities for light exciting electrons from hh and lh bands is fundamentally fixed.
A. No. The 3 times is parameter, which is valid only within approximation of the Luttinger-Kohn model. My opinion is that the difference is smaller in real cases. I have grown and studied a GaAs/AlGaAs compressive- strained QW LD, where light is emitted due to the electron transition ee->hh and a GaAs/GaAsP tensile-strained QW LD, where light is emitted due to the electron transition ee->lh. I have not notice a striking difference in the lasering efficiency.
Even difference in absorption coefficients of the direct-band semiconductor GaAs and the indirect-band semiconductor Si is only 10 times (27424 cm-1 and 2345 cm-1 at l=700 nm), therefore the 3-time difference between lh and hl is too large.
Q. Why there is 3-time difference of excitement probabilities for electrons from heavy-hole and light-hole bands.
It is because of different symmetry of electrons of the heavy-hole and light-hole bands.
With which electrons light interacts more effectively? With conduction electrons or with localized d-electrons?A. Light interacts more effectively with conduction electrons, because their larger size.
Interaction between two particles are most effective when they have the same size. The size of a photon is about 0.1 mm -1 mm (from a light bulb) and 1 mm -1 m (from a laser). The size an electron is substantially smaller. The length of a conduction electrons is called the mean-free path λ mean. The size of a conduction electrons ( λ mean) is about 30-200 nm in a semiconductor and 0.5~20 nm in a metal. The size of a localized d-electron is about the size of atomic orbital ~0.1 nm. As a result, the interaction of a photon with a conduction electron is more effective than with a localized electron.
Efficiency reduction at higher spin-polarization of the electron gas.
From linearly-polarized light, which is spin-unpolarized, a quater-wave plate may create circulary polarized light, which is spin-polarized.
standing wave
unpolarized light
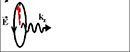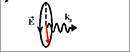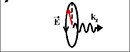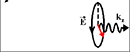(about timescale of the Kerr and Faraday effects)
(from Chen Xiao) The magneto-optical effects such as KERR or FARADAY rotation have been popular techniques to probe magnetism. The timescale of MO effects might be a few femtoseconds. Would it be possible to detect the AHE in the dynamical regime? (It is noticed that G. Sala et al. achieve a time- resolved hall-effect detection in the nanosecond range.)
According to the classical Quantum Mechanic any Magneto-optical effect (Faraday, Kerr and MCD effects) has no timescale. They are infinitely fast. The Faraday, Kerr and MCD effects all originate from a Zeeman splitting of the energy level in a magnetic field. The energy level and the Zeeman splitting exists primarily of any dynamics. Therefore, it is meaningless to assign any dynamics to the energy level.
Of course, a change of some external parameter may change the strength of the magneto-optical (MO) effect. However, the effect timescale is determined by the timescale of the external parameter, but not by the timescale of MO effect. For example, the MO strength depends on the strength of the external or internal magnetic field, under a change of the magnetic field the MO strength changes. The timescale of this process is determined only by the timescale of the change of the magnetic field. The timescaly of MO effect itself is instant.
Another example is a filling of one of Zeeman-split energy levels by the spin- polarized electrons. This event also changes the MO strength. Similarly, only the speed of the filling or emptying of the energy level determines the timescale in this case.
Also, there is a timescale of the optically- induced electron transition from one level to another. This timescale is very short and equals to a half of the period of a Rabi oscillation.
I will try to answer your questions as soon as possible
Content 
