Dr. Vadym Zayets
v.zayets(at)gmail.com
My Research and Inventions
click here to see all content |

Dr. Vadym Zayetsv.zayets(at)gmail.com |
|
 |
more Chapters on this topic:IntroductionScatteringsSpin-polarized/ unpolarized electronsSpin statisticselectron gas in Magnetic FieldFerromagnetic metalsSpin TorqueSpin-Torque CurrentSpin-Transfer TorqueQuantum Nature of SpinQuestions & Answers
more Chapters on this topic:IntroductionScatteringsSpin-polarized/ unpolarized electronsSpin statisticselectron gas in Magnetic FieldFerromagnetic metalsSpin TorqueSpin-Torque CurrentSpin-Transfer TorqueQuantum Nature of SpinQuestions & Answers
more Chapters on this topic:IntroductionScatteringsSpin-polarized/ unpolarized electronsSpin statisticselectron gas in Magnetic FieldFerromagnetic metalsSpin TorqueSpin-Torque CurrentSpin-Transfer TorqueQuantum Nature of SpinQuestions & Answers
more Chapters on this topic:IntroductionScatteringsSpin-polarized/ unpolarized electronsSpin statisticselectron gas in Magnetic FieldFerromagnetic metalsSpin TorqueSpin-Torque CurrentSpin-Transfer TorqueQuantum Nature of SpinQuestions & Answers
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
|
Spin and Charge Transport
Spin-Torque CurrentThe spin-torque current is a current flowing between regions, which have different spin directions of the spin-polarized electrons. The spin-torque current induces a spin torque on the spin-polarized electrons. The torque rotates spin directions in neighbor regions toward each other. The spin-torque current aligns the spins of all spin-polarized electrons in one direction over the whole sample. In contrast to the spin current, which is the diffusion of the spin accumulation, the spin-torque current is the diffusion of the direction of the spin accumulation.
|
 |
Fig.1 Animated picture. Spin accumulation current. Conventional spin current. |
Spin accumulation current is the current of spins. The spins diffuse from a region of higher spin accumulation into a region of smaller spin accumulation.
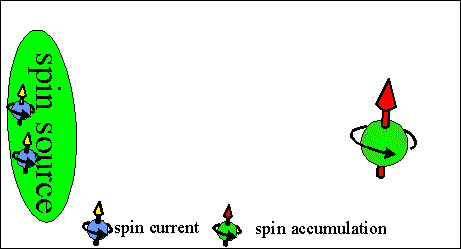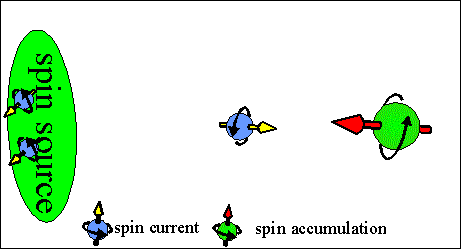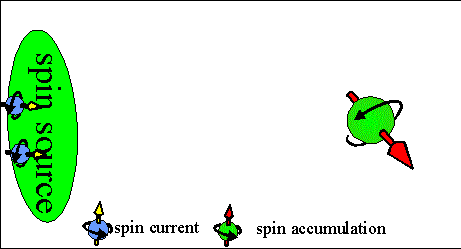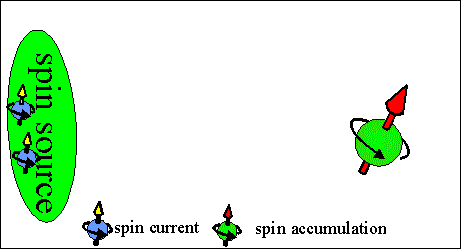 |
Fig.2 Animated picture. Spin-torque current. |
Spin-torque current is the current of the spin direction. The spin direction diffuses between regions of different directions of spin accumulation. The spin-torque current aligns spins in neighboring region in one directions.
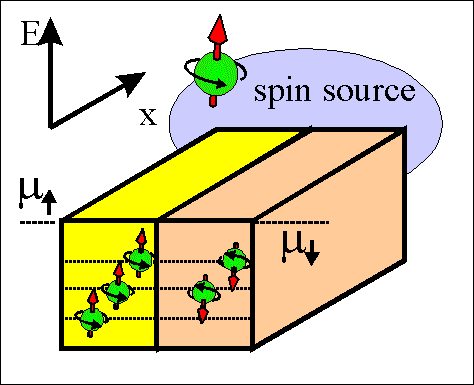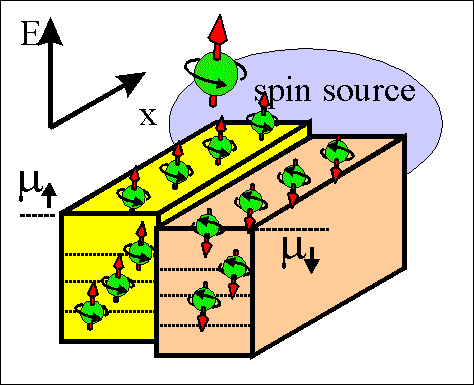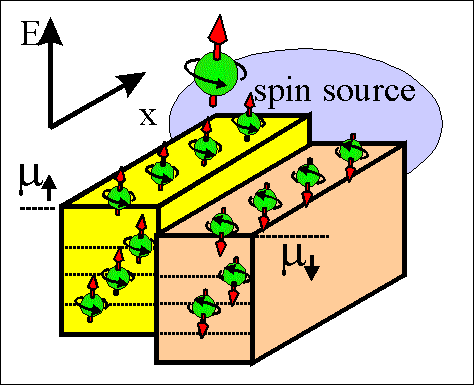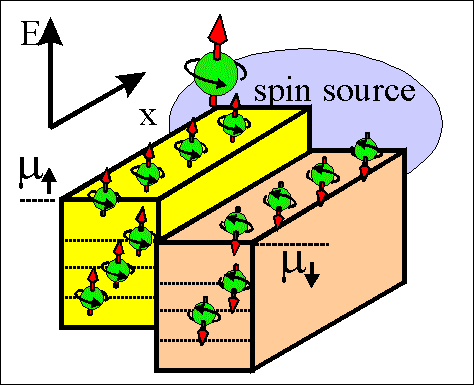 |
Fig.3 Animated picture. Spin accumulation current. Conventional spin current. |
The spin accumulation current flows from a region of higher spin accumulation to a region of lower spin accumulation.
The spin accumulation current requires a spin source, but it does not require a spin drain.
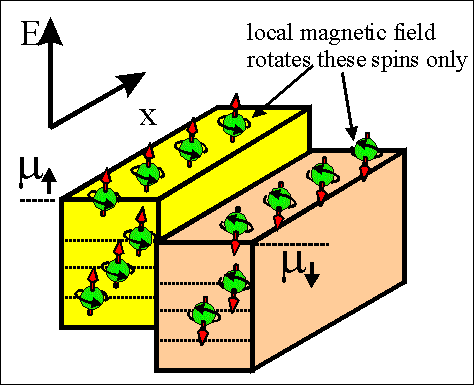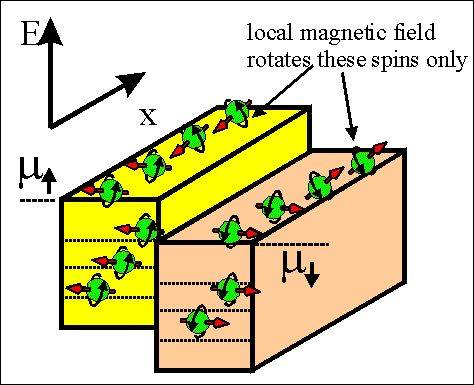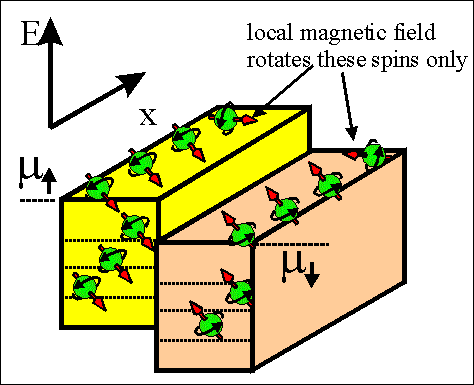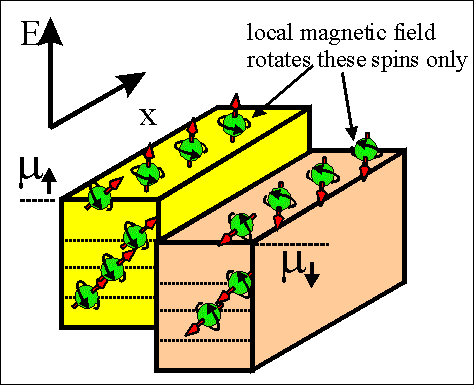 |
Fig.4Animated picture. Spin torque current. |
The spin torque current flows between regions in which spin directions of spin-accumulated electrons are different.
The spin torque is trying to make spins aligned either parallel or antiparallel over whole sample.
1) The spin-torque current is trying to align spins of all spin-polarized electrons in one direction over the whole sample.
2) The spin-torque current is greater in a metal with a shorter spin diffusion length
3) The spin-torque current is always accompanied by an additional spin relaxation. This means that the spin life time becomes shorter in regions where the spin-torque current flows.
The results in short
In the case when there is a spacial gradient of spin direction of spin-polarized electrons, the spin-polarized electrons experience the spin torque, which can be calculated as
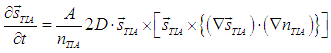
and there is a spin relaxation (conversion of electrons from the group of spin-polarized electrons into the group of spin-polarized electrons) associated with spin-torque current with rate:
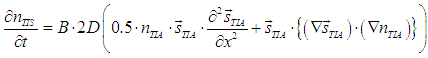
where ![]() is a unit vector along the spin direction of the spin-polarized electrons,
is a unit vector along the spin direction of the spin-polarized electrons, ![]() is the spacial density of spin-polarized electrons and D is the diffusion coefficient.
is the spacial density of spin-polarized electrons and D is the diffusion coefficient.
If the spin directions of spin-polarized electrons are different in two close regions in a metal, there is a mutual diffusion of electrons between these two regions. Since the spin direction of the diffused electrons is different, they cause a spin torque (For details about the spin torque, click here), which rotates the spin direction of the spin-polarized electrons. Because of this spin torque, the spin directions of each region are turning toward each other.
Charge current -> flow of charge
Spin current -> flow of spin
Spin-torque current -> flow of spin direction
1) The spin torque due an electron diffusion from the surroundings.
2) Additional rate of the spin relaxation, because of the spin-torque current.
This is because the spin torque is always accompanied by an additional spin relaxation
The spin-torque and the spin relaxation are linearly proportional to the diffusion rate of the electrons (Details, see here).
This injection rate was calculated from the random-walk model. The method is similar to the method described here (see derivation of Derivation of Fick's 1st law in 1 dimension)
We will consider a spin current as a diffusion of uncharged particles, which have a defined spin direction. In this case, the random walk approximation may be used.
We assume that the diffusion rate of the spin-polarized electrons does not depend on the amount of spin-polarized electrons.
Let us consider the spin diffusion between 3 points: ![]() , where
, where ![]() . Each point has a different spin direction and a different amount of spin-polarized electrons. As a result of the random walk, the number of particles, which diffuse from a point in some direction (for example, from point x towards point
. Each point has a different spin direction and a different amount of spin-polarized electrons. As a result of the random walk, the number of particles, which diffuse from a point in some direction (for example, from point x towards point ![]() ) is proportional to the number of particles at that point
) is proportional to the number of particles at that point
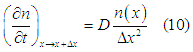
where D is the diffusion constant and n(x) is the density of particles at point x.
In the case when spin relaxation is weak and the conversion of electrons from the spin relaxation is slow, it is possible to assume that the diffusion of spin-polarized and spin-unpolarized electrons are independent. Than, the number of spin-polarized electrons, which diffuse from point ![]() to point x, is calculated as
to point x, is calculated as
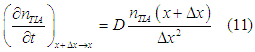
The number and spin direction of spin-polarized electrons at point ![]() can be approximated as
can be approximated as
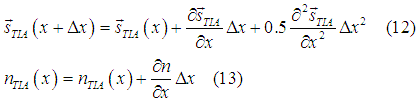
Since the spin direction at points x and ![]() are different, electrons, that diffuse from point
are different, electrons, that diffuse from point ![]() cause a spin torque on the electrons at point x. The spin torque can be calculated by substitution Eqs (11),(12),(13) into Eq(20) here
cause a spin torque on the electrons at point x. The spin torque can be calculated by substitution Eqs (11),(12),(13) into Eq(20) here
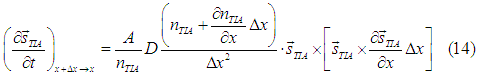
The spin torque is accompanied by spin relaxation (conversion of electrons from the group of spin-polarized electrons to the group of spin-unpolarized electrons). The conversion rate is calculated by substitution Eqs (11),(12),(13) into Eq(21) here
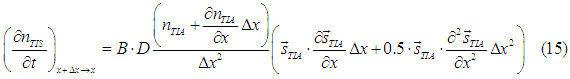
Electrons also diffuse from point x-delta_x towards point x. Similarly, the spin torque due to diffusion in this direction is calculated as
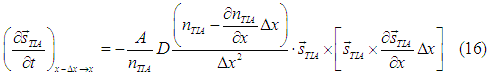
and the spin relaxation can be calculated as
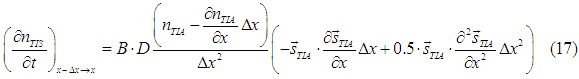
Summing up Eqs. (14) and (16), the spin torque, which the spin-polarized electrons experience due to the diffusion from the surroundings, can be calculated as
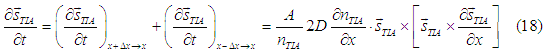
The spin relaxation due to the spin-torque current can be calculated as
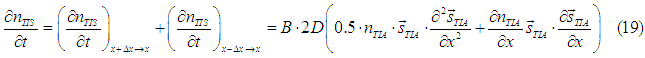
The case when the spin accumulation exponentially decays along the diffusion distance
In this case of the exponential decay along the x -coordinate, the number of spin-polarized electrons are
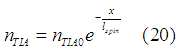
where ![]() is the spin diffusion length.
is the spin diffusion length.
Substituting Eq.(2) into Eqs. (18) and (19), the spin torque and the spin relaxation rate are obtained as
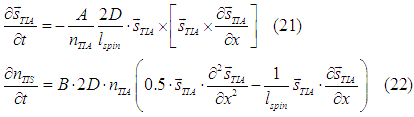
For the similar method check Derivation of Fick's 1st law in 1 dimension
Here it is assumed that the diffusion of spin-polarized and spin-unpolarized electrons are independent.
Firstly, we calculate an amount of spin-polarized electrons, which diffuse from point x out to surrounding.
According to the random-walk model, the electrons diffuse from point x to the left at the rate:
![]()
The electrons diffuse from the point x to the right at the rate
![]()
From Eqs. (p0a) and (p0b) the number of spin-polarized electrons, which diffuse out of point x per unit time, is
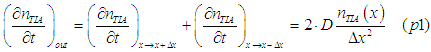
Secondly, we calculate an amount of spin-polarized electrons, which diffuse from surrounding into point x.
Electrons diffuse into point x from points x+delta_x and x-delta_x. The number of spin-polarized electrons, which diffuse into point x per unit time, is
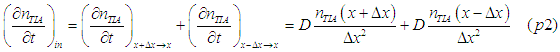
There is an additional spin relaxation due to the spin-torque current. The number of electrons, which are converted at point x from the group of spin polarized electron into the group of the spin-unpolarized electrons, is
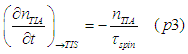
where ![]() is the spin life time.
is the spin life time.
The continuity equation for the spin-polarized electrons at point x will be
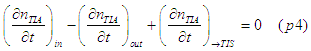
Substituting (p1)-(p3) into (p4) gives
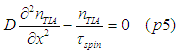
Defining the spin diffusion length as
![]()
the spin diffusion equation is obtained from Eq. (p5) as
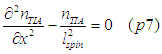
I will try to answer your questions as soon as possible