Dr. Vadym Zayets
v.zayets(at)gmail.com
My Research and Inventions
click here to see all content |

Dr. Vadym Zayetsv.zayets(at)gmail.com |
|
 |
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionScatteringsSpin-polarized/ unpolarized electronsSpin statisticselectron gas in Magnetic FieldFerromagnetic metalsSpin TorqueSpin-Torque CurrentSpin-Transfer TorqueQuantum Nature of SpinQuestions & Answers
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
|
Ordinary Hall Effect
Spin and Charge TransportThe Ordinary Hall effect occurs when a magnetic field is applied perpendicularly to the direction of an electron current. The Lorentz force is the origin of the ordinary Hall effect. Moving electrons in an magnetic field experience an effective electrical field perpendicularly to their movement, which turns them from a straight path. As a result, a charged is accumulated at sides of wire and a voltage is built up perpendicularly to the wire, which is called the Hall voltage.Electrons and holes moves in opposite directions. As a result, the ordinary Hall is of opposite polarity for the electrons and holes. In a semiconductor, carriers are either electrons or holes. Therefore, the Ordinary Hall effect is large in a semiconductor. In a metal, there are nearly-equal numbers of electrons and holes and therefore the ordinary Hall effect in a metal is a small.In a ferromagnetic metal, the Ordinary Hall effect creates a spin accumulation at the side of a ferromagnetic wire. As a result, the spin polarization becomes larger than the equilibrium spin polarization at one side of the wire and smaller at another side of the wire. This effect is substantial in a metal, because the contribution to this effect from holes and electrons are of the same polarity.
|
Measurement of Ordinary Hall effect |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
| click on image to enlarge it |
. ![]() DC measurement using a Hall Bar
DC measurement using a Hall Bar
The ordinary Hall effect is evaluated by measuring a voltage on side of the wire (the Hall voltage VHall). From the measured Hall voltage, the Hall angle αHall is evaluated as ( ![]() See HallAMRbasic.pdf):
See HallAMRbasic.pdf):
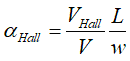
where V is the voltage applied to the wire, w is the width of the wire and L is the length of the wire.
(features of measurements) ![]()
(a non-magnetic metal) : The OHE is only one Hall effect from the family of the Hall effects, which occurs in a non-magnetic metal and a semiconductors. The dependence of the Hall angle vs external magnetic field H is is nearly perfectly linear. There are a very weak deviation from linear dependence (See below)
(a ferromagnetic metal): Additionally to OHE, the Anomalous Hall effect (AHE) and the Inverse Spin Hall effect (ISHE) also contribute to the Hall voltage. The distinguish feature of OHE is its linear dependence on an external magnetic field H (see here) . At a low external magnetic field, the OHE contribution is substantially smaller than AHE and ISHE contribution. At a high magnetic field, the OHE contribution becomes dominated.
 |
| Relativistic origin of the Lorentz force (Hall effect). An object (red) is moving in a static magnetic field. In the coordinate system moving together with the object, the static magnetic field is relativistically transformed into the effective magnetic field Heff and the effective electrical field Eeff. In case if the particle is charged, it experiences the force from the effective electrical field Eeff (the Lorentz force). |
According to the Theory of The Relativity the electric and magnetic field mutually transformed into each other depending on the speed of an observer. For example, if in a coordinate system of static observer there is only a magnetic field, a movable observer will experience this field as both an electrical field and a magnetic field.
A particle moving in a static magnetic field experiences an effective electric field. The effective electrical field acts on the particle charge (the Lorentz force, Hall effect) and forces the particle to move along this field.
A particle moving in a static electrical field experiences an effective magnetic field. The effective magnetic field acts on the particle magnetic moment (spin-orbit interaction) and causes the precession of the magnetic moment around the direction of the effective magnetic field.
the Hall effect ==== results in ====> an effective electrical field
| The Lorentz force- tween effect with the effect of the spin-orbit interaction | ||||
|
the Spin-Orbit interaction ===results in=====> an effective magnetic field
The effective electrical field due to the Hall effect does not depend either on the particle charge or the particle spin. it is only depend on the particle movement direction and the direction of the magnetic field !!!!
 Ordinary Hall effect describes a generation of an electrical current, which flowing perpendicularly
Ordinary Hall effect describes a generation of an electrical current, which flowing perpendicularly
Results in short: Ordinary Hall in semiconductors and metals
 |
 |
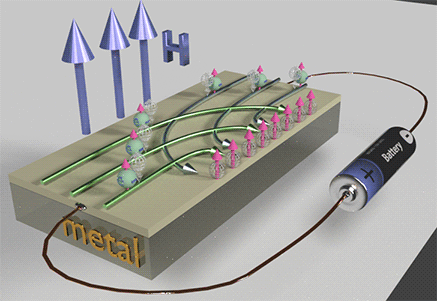 |
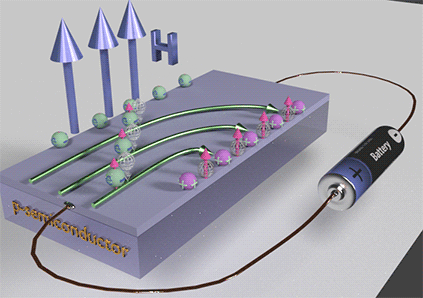
| Hall effect in n-type semiconductor. There is a spin accumulation at the right side, where there is an accumulation of the negative charge. There is no spin accumulation at the right side of the sample. | Hall effect in p-type semiconductor. There is a spin accumulation at the right side, where there is an accumulation of the positive charge. There is no spin accumulation at the right side of the sample. | Hall effect in metal. There is a spin accumulation at the right side. However. there is almost no charge accumulation!! |
![]() How the calculations are done:
How the calculations are done:
(step 1) Without an electrical field, the distribution of electron movement direction is a sphere Fi,0.
(step 2) In an electrical field, the electron are accelerating and gaining energy. As a result, there are more electrons moving along the electrical field than opposite to the field. The distribution sphere is shifted along the electrical field.
(step 3) In a magnetic field, the electron direction is turn slightly by the Lorentz force with respect to direction of magnetic field (Eq.(1.2)). This causes a rotation of the distribution of electron movement directions with the pivot point at the axes origin.
(step 4) When there is no electrical field and the distribution field is a sphere at center of coordinate origin. Under a magnetic field, the sphere is rotates. However, since the rotation center is at the center of the sphere, the rotation does not change the distribution. (Eq. (1.4))
(step 5) When there is an electrical field, the distribution is shifted from the center along along the electrical field. Under a magnetic field the distribution is rotated. Since the center of the sphere is shifted from the rotation center, . However, since the rotation center is at the center of the sphere, the rotation does not change the distribution. (Eq. (1.4))
--------------------
The Hall effect can be described by the force term (See Fig.7b) in the Boltzmann transport equations
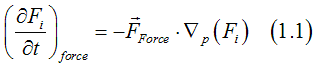
where
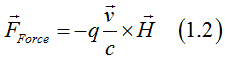
In an equilibrium in the electron gas the electrons move in all direction. Since the Lorentz force only changes the electron movement direction, the Lorentz force does not change the equilibrium electron distribution Fi,0
![]()
Eq. (1.3) can be verified as follows (See Fig.7d)
Only if there is an electron current , the Lorentz force may change the electron distribution. The change of the electron when there is an electron current, was calculated here. Substituting this distribution ( Eq. (14.7) ) into Eq.(1.1) gives
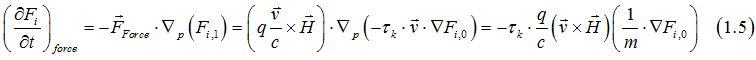
Using the relaxation-time approximation Eqs. (9),(12), ignoring the term of order H2 and substituting Eq. (1.5) into the Boltzmann equations Eqs. (18) gives
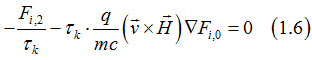
From Eq. (1.6) the Hall current can be calculated as (See Eq.(11.3) here)
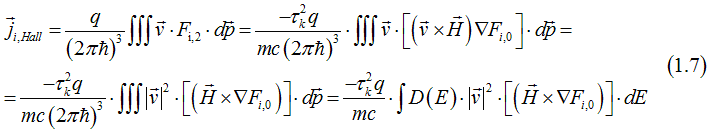
or Hall current can be calculated as
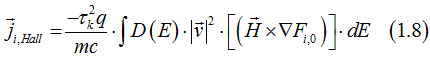
| Influence of magnetic field and electrical current on distribution of electron movement directions | ||||||||||||
|
||||||||||||
| The length of a vector from axis origin to sphere is proportional to the number of electrons moving in the vector direction. | ||||||||||||
| The red sphere shows the distribution of electron movement directions. The red sphere shows the distribution in the of no current and no magnetic field | ||||||||||||
| click on image to enlarge it |
![]() What an electrical field do for the movement-direction distribution: The distribution is shifted along the electrical field direction
What an electrical field do for the movement-direction distribution: The distribution is shifted along the electrical field direction
In an electrical field, an electron is accelerating along electrical field. Therefore, the speed and energy increase for electron moving along the electrical field and decrease for electron moving opposite to the field. E.g. an electrical field Ex along x-axis makes the scattering probability towards +x-direction higher than in -x- direction p(+x)>p(-x). As a result, the number of electrons moving in the +x- directions becomes larger.
![]() What an magnetic field do for the movement-direction distribution: The distribution is rotated around magnetic field, The rotation canter is the axis origin
What an magnetic field do for the movement-direction distribution: The distribution is rotated around magnetic field, The rotation canter is the axis origin
The graph describes the directional distribution of electrons. The length of a vector from axis origin to sphere is proportional to the number of electrons moving in the vector direction. Usually the distribution is a sphere, which center is at the axis origin (Fig.7.a). In this case, the electrons are equally distributed in all directions and the number of electrons moving in each direction is equal.
The conduction electrons experience very frequent scatterings. At room temperature an electron experiences more than one scattering in one picosecond (1E-12 s). The scatterings are directional independent and they mix up electrons in all directions. Due the scatterings, the number of electrons moving in each direction is equal for any direction.
A conduction electron is accelerated in an electrical field along the direction of the field.
Yes. The electron scatterings in a solid are frequent (~one scattering per 1ps at room T).
No. E.g. in case of quantum well (QW), the electron cannot move perpendicular to QW, therefore the distribution is 2D circle. In case of an anisotropic material the distribution can be of ellipse shape. However, in most of materials the distribution is a sphere ( or close to a sphere).
It is important. When there is no current, the numbers of electrons moving in any two opposite directions are equal.
In the case when a magnetic field is applied perpendicularly to the flow direction of a drift current, the charge carriers experience the Lorentz force in the direction perpendicular to both the magnetic field and the current. Because of this force, the carriers are accumulated at the edges of the sample and a voltage transverse to the drift current is built up. This voltage is called the Hall voltage. In n- and p-type semiconductors the Hall voltage is of opposite sign, because the holes and electrons are accumulated at the same side of sample, but they have opposite charge (Figs.14-15). Because of a nearly- equal number of holes and electrons in a metal, the Hall voltage in the metal is small and it is proportional to the gradient of the density of states at the Fermi level. When the electron gas in a metal is spin-polarized, both the electrons and holes are spin-polarized. Because of the Hall effect, the spin-polarized electrons and holes are accumulated at the same side of the sample. Therefore, at this side of sample a significant spin accumulation occurs. (Fig.16)
In a n-type semiconductor there is only one type of carries. It is the electrons, which energy is above the Fermi energy.
The electrons diffuse from a "-" source toward a "+" drain. As they diffuse, the magnetic field turns them to the left with respect to their movement direction.
As a result, both the spin and the negative charge are accumulated at the right side of the wire.
At the left side of the wire, both the spin and the negative charge are depleted
 It is relatively safe to use oversimplified classical description of the Ordinary Hall effect for a n-type semiconductor.
It is relatively safe to use oversimplified classical description of the Ordinary Hall effect for a n-type semiconductor.
In the case of a n-type semiconductor:
(no limitation 1) the most of conduction electrons solely occupy one quantum state. There are a very few states, which are occupied by two electrons of opposite spins (See here)
(no limitation 2) there are a lot of unoccupied quantum states above the Fermi level (See here). Therefore, there are no limitation for an electron to change its speed, movement direction or energy.
In a p-type semiconductor, there are two types of carries:
(1st type of carries): Holes are the carriers for the Spin and the Charge.
The holes are the conduction electrons, which energy below EFermi. They move from a positive- voltage source to negative-voltage drain similar as a positively- charged particle does (See here details)
The holes diffuse from a "+" source toward a "-" drain. As they diffuse in the magnetic field they turn to the right.
The current of "full" states is the normal current.
This means that the negatively charged "full" states diffuses from a "-" source toward a "+" drain.
Due to the Hall effect they should turn to the left (similar to the electrons shown in Fig. 14).
However, the most of the electrons, which occupies the "full" states, are the standing-wave electrons. (See Fig.9 here)
The standing-wave electrons do not move, therefore they do not contribute to the Hall current.
In contrast, the electrons, which occupies the "spin" states, are the running-wave electrons.
For this reason, mostly the "spin" states contribute to the Hall effect in the case of the hole current.
|
||
Fig. 15. Hall effect in a p-type semiconductor. Magnetic field is applied perpendicular to the film (blue arrows). There is only an electron current green arrows show path of holes, which transfer a positive charge and spin. The positive charge and spin are accumulated at the right side of the wire. At left side of the wire, a negative charge accumulated and the spin is depleted |
|
||
Fig. 16. The Ordinary Hall effect in metal. The electron current (green balls) flows from “-” to “+” . In a magnetic field the electrons turn left in respect to direction of their movement. The holes current (blue balls) flows from “+” to “-” . In a magnetic field the holes turn right in respect to direction of their movement. Therefore, the charge does not accumulate. In contrast, the spin is accumulated at one edge of the sample. |
The drift current in a metal consists of the electron and hole currents, which flow in the opposite direction. Since the charge of an electron and a hole is opposite, the direction of the charge transport is the same for the electron and hole current. This is the transport of the "-" charge from "-" to "+". Or what is the same, the transport of the"+" charge from "+" to "-".
Since the electrons and holes move in the opposite directions, in the magnetic field the electrons turn to the left and holes turn to the right.
As result, both the electrons and the holes are accumulated at the same side of the wire. At the opposite side of the wire, both the electrons and holes are depleted.
Since the charge of an electron and a hole is opposite, the charge is not accumulated. This is the reason why the Hall voltage in a metal is small.
In contrast, the spin direction of electrons and holes is the same, therefore there is a significant spin accumulation at opposite side of the wire due to the Ordinary Hall effect in a metal.
 |
Fig. 17. Ordinary Hall effect in a metal. Magnetic field is applied perpendicular to the film (blue arrows). Green arrows, which are directed from "-" to "+", show path of spin-polarized electrons. They accumulate the negative charge and up- spin at the right side of the metallic wire. Green arrows, which are directed from "+" to "-", show path of spin-polarized holes. They accumulate the positive charge and up- spin at the right side of the metallic wire. As a result, there is a spin accumulation, but there is no charge accumulation at |
(What it is about) ![]() The conduction electrons in a ferromagnetic metal are spin-polarized. Due to the Ordinary Hall effect, the spin polarization becomes larger than the equilibrium spin polarization at one side of ferromagnetic wire and smaller at another side.
The conduction electrons in a ferromagnetic metal are spin-polarized. Due to the Ordinary Hall effect, the spin polarization becomes larger than the equilibrium spin polarization at one side of ferromagnetic wire and smaller at another side.
(Origin of the effect)  In ferromagnetic metal, both the electrons and holes are spin- polarized. Due to the Ordinary Hall effect the electrons and holes are accumulated at the same side of the ferromagnetic wire. The accumulation of the spin-polarized electrons and holes creates the spin accumulation at a side of a ferromagnetic metal due to the Ordinary Hall effect.
In ferromagnetic metal, both the electrons and holes are spin- polarized. Due to the Ordinary Hall effect the electrons and holes are accumulated at the same side of the ferromagnetic wire. The accumulation of the spin-polarized electrons and holes creates the spin accumulation at a side of a ferromagnetic metal due to the Ordinary Hall effect.
(Direction of the created spin accumulation) ![]()
![]()
![]()
 The direction of spin polarization, which is created by the Ordinary Hall effect, is exactly the same as the spin direction of the equilibrium spin polarization in the nanomagnet
The direction of spin polarization, which is created by the Ordinary Hall effect, is exactly the same as the spin direction of the equilibrium spin polarization in the nanomagnet
(Why is it relevant?) ![]() The conduction electrons in a ferromagnetic wire are already spin- polarized. Even though the Ordinary Hall effect makes the spin polarization slightly smaller and slightly larger than the equilibrium spin polarization in some places, what difference does it make? In the average the spin polarization is still nearly the same as in the equilibrium?
The conduction electrons in a ferromagnetic wire are already spin- polarized. Even though the Ordinary Hall effect makes the spin polarization slightly smaller and slightly larger than the equilibrium spin polarization in some places, what difference does it make? In the average the spin polarization is still nearly the same as in the equilibrium?
(Answer: it creates the pump torque for a spin precession and magnetization reversal) ![]() An increase or a decrease of spin polarization at an interface of a nanomagnet influences the magnetic properties of the nanomagnet such as the Perpendicular Magnetic Anisotropy (PMA) . Also, additional spin polarization increase the magnetic field, which is induced by the spin- polarized electrons (See here). It is important that both changes are created and can modulated by the electrical current. This featured makes possible the parametric enhancement of magnetization precession and the parametric magnetization reversal in a nanomagnet. For parametric magnetization reversal due to modulation of the anisotropy field (see here) and due to modulation of the magnetic field, which is induced by the spin polarization, see here.
An increase or a decrease of spin polarization at an interface of a nanomagnet influences the magnetic properties of the nanomagnet such as the Perpendicular Magnetic Anisotropy (PMA) . Also, additional spin polarization increase the magnetic field, which is induced by the spin- polarized electrons (See here). It is important that both changes are created and can modulated by the electrical current. This featured makes possible the parametric enhancement of magnetization precession and the parametric magnetization reversal in a nanomagnet. For parametric magnetization reversal due to modulation of the anisotropy field (see here) and due to modulation of the magnetic field, which is induced by the spin polarization, see here.
(comparison with another mechanism of spin accumulation) ![]()
![]()
![]()

![]()
![]()
![]()

![]()
![]()
![]() The distinguish feature of the spin accumulation due the Ordinary Hall effect is that it is substantially larger than another known types of the spin accumulation such as the Spin Hall effect and the spin- dependent scatterings across an interface.
The distinguish feature of the spin accumulation due the Ordinary Hall effect is that it is substantially larger than another known types of the spin accumulation such as the Spin Hall effect and the spin- dependent scatterings across an interface.
Since the charge of electrons and holes is opposite and there are nearly- equal numbers of the holes and electrons in metal, the charge accumulation and therefore the Hall voltage are very small in a metal. In contrast, the spin direction of the electrons and the holes is the same in a ferromagnetic metal. Spin-polarized electrons accumulated at sides of wire due to spin accumulation of the spin-polarized electrons and holes is the the same. .
The spin-polarized electrons and spin-polarized holes are the similar objects. Both are the electrons which occupies solely one quantum state (max occupance is two electrons of opposite spins)
Only difference between electrons and holes is their energy with respect to the Fermi energy EFermi.
The energy of electrons is higher than EFermi and the energy of holes is lower than EFermi.
The number of electrons, which solely occupies one quantum state, increases below EFermi. and decreases above EFermi.. This causes that the electrons moves from "-" to "+" voltage similar to negatively-charged particles. In contrast, the holes moves from "+" to "-" voltage similar to positively-charged particles. See more details here.
Since the electrons and holes move in the opposite directions, they turn in the opposite directions due the Lorentz force and contribute oppositely to the Ordinary Hall effect.
The electrons turn to the left and the holes turn to the right, but they move in opposite directions. As a result, both the positive and negative charge is accumulated at the same side of wire and in total there is no charge accumulation. It is different for the spin comparing to the charge. If the electrons and holes have the opposite charge, they have the same direction of the spin for spin-polarized electrons. Therefore, the spin is accumulating at side of a metallic wire due to the Ordinary Hall effect and this type of the spin accumulation is very effective.
 General Notes about the Ordinary Hall effect in a metal
General Notes about the Ordinary Hall effect in a metal
1. The Ordinary Hall effect in a metal is small, but it is not zero.
It can be positive and negative. It depends on whether the electron or hole current is larger in a metal.
The Hall voltage in a metal is proportional to the energy derivative of the density of states at the Fermi energy. (See here)
2. The Ordinary Hall effect is larger in a crystalline metal, but is very small (close to zero) in an amorphous metal.
From my experimental measurements, I have noticed that the strength of the Ordinary Hall effect substantially depends on the crystal quality of the metal. For example, a boron diffusion usually transforms a metal from a crystalline to amorphous phase. Usually this phase transformation leads to a reduction of the Ordinary Hall effect.
3. From the Hall voltage of the Ordinary Hall effect in a metal, the injection conductivity σinjection can be estimated.
The effectiveness of spin injection and The injection conductivity σinjection is proportional to the Hall voltage.
4. For a larger the spin torque or a better spin injection efficiency, a metal having largest the Hall voltage should be used.
Similarity between the spin transport (spin injection) and the Ordinary Hall effect is that the contributions of holes and electrons are opposite for both effects. Since in a metal the number of the
A. An electrical current in a metal consists of two nearly-equal currents: electron current and hole current. The electron and hole currents transform the spin in opposite directions. The electron current transforms the spin from a negative to a positive voltage as negatively-charged particles with spin do. The hole current transforms the spin in opposite direction from a positive to a negative voltage as positively-charged particles with spin do. In the case when the electron and hole currents are exactly the same, the spin cannot be transformed by an electrical current from one point of a metal to another point or the same there is no spin-injection effect in a metal. For an effective spin injection the largest unbalance between electron and hole currents is required.
Similarly, the electron and hole current have opposite contribution to the ordinary Hall effect (OHE). In the case when electron and hole currents are the same, the Hall angle of OHE is zero and there is no any spin injection effect. When electron and hole currents are different, the Hall angle of OHE becomes larger and spin injection effect becomes effective.
Conductivity is of electron-type
moderate conductivity~ 0.08 E7 S/m
Hall coefficient ~ - 0.3 mdeg/kG
Metal: Au |
||||||||
|---|---|---|---|---|---|---|---|---|
|
||||||||
| black line : scan from - 7kG to+ 7 kG. red line:scan from +7kG to - 7 kG | ||||||||
| sample Ref9: SiO2:Ta(0.1 nm):Au(5 nm) | ||||||||
| click on image to enlarge it. Measurement date: 2019.11 |
Conductivity is of hole-type
good conductivity ~ 0.5 E7 S/m
Hall coefficient ~ + 4 mdeg/kG
Metal: Ru |
||||||||
|---|---|---|---|---|---|---|---|---|
|
||||||||
| black line : scan from - 7kG to+ 7 kG. red line:scan from +7kG to - 7 kG | ||||||||
| sample Ref30: SiO2:Ta(0.4):Ru(25) | ||||||||
| click on image to enlarge it. Measurement date: 2019.11 |
Conductivity is of electron-type
good conductivity ~ 0.67 E7 S/m
Hall coefficient ~ -4 mdeg/kG
Metal: Ir |
||||
|---|---|---|---|---|
|
||||
| black line : scan from - 7kG to+ 7 kG. red line:scan from +7kG to - 7 kG | ||||
| sample Ref31: SiO2:Ta(0.4)/Ir(25)/Ru(1) | ||||
| click on image to enlarge it. Measurement date: 2019.11 |
Conductivity is of electron-type
bad conductivity ~ 0.036 E7 S/m
Hall coefficient ~ -0.015 mdeg/kG
A. As 2019, the origin of these oscillations is unclear. There are also oscillations in 1st and 2d derivations of the Hall angle of the Anomalous Hall effect in a ferromagnetic metals. Maybe this is a similar oscillations. Their physical origin still has to be clarified.
Summary
Metals with hole-dominated transport
(spin is drifted from "+" to "-")
| metal | Cu | Ag | Au | Al | Pt | Mg | Pd | Gd | Tb | |
|---|---|---|---|---|---|---|---|---|---|---|
Hall coefficient (* 1E-11 Ohm*m/T) |
-5.12 | -8.81 | -7.16 | -3.44 | -2.2 | -8.3 | -7.6 | -37 | -44 | |
| Conductivity (*1E7 S/m) | 5.96 | 6.21 | 4.1 | 3.5 | 0.96 | 2.27 | 0.95 | 0.076 | 0.087 | |
| Hall angle/B (*mrad/T) | -3.05 | -5.471 | -2.935 | -1.204 | -0.211 | -1.884 | -0.722 | -0.281 | -0.3828 | |
| Hall angle/B (*mdeg/T) | -174.75 | 313.47 | -168.16 | -68.984 | -12.089 | -107.95 | -41.368 | -16.1 | -21.933 | |
| crystal structure | fcc | fcc | fcc | fcc | fcc | hcp | fcc | cph | hcp |
Metals with electron-dominated transport
(spin is drifted from "-" to "+")
| metal | Ta | Ru | Cr | Rh | W | V | Zn | Mo | Nb | |
|---|---|---|---|---|---|---|---|---|---|---|
Hall coefficient (* 1E-11 Ohm m/T) |
10.1 | 22 | 37.9 | 5.05 | 10.8 | 8.2 | 20(2) | 18 | 9 | |
| Conductivity (*1E7 S/m) | 0.76 | 1.40 | 0.8 | 0.0211 | 1.79 | 0.5 | ||||
| Hall angle/B (mrad/T) | 0.7676 | 3.08 | 3.032 | 0.01 | 1.933 | 0.41 | ||||
| Hall angle/B (mdeg/T) | 43.98 | 176.47 | 173.72 | 0.57296 | 110.75 | 23.491 | ||||
| crystal structure | bcc | hcp | bcc | fcc | bcc | bcc | hcp | bcc | bcc |
The transport is electron-dominated.
Hall coefficient at 6T is 1E9 B* kG/Ohm/cm
non-ordinary Hall coefficient is Rs=30-40E-11 Ohm*m/T at RT (Hall angle=3-4E-3 1/T), it decreases almost to zero at lower T
ordinary Hall coefficient is 2E-11 Ohm*m/T at RT (Hall angle=0.2E-3 1/T), it weakly decreases at lower T.
Conductivity : 1.01E7(S/m)
bcc structure
Transport is ???-dominated. (maybe hole-dominated)
non-ordinary Hall coefficient is small positive Rs=2E-11 Ohm*m/T at RT(Hall angle=0.32E-3 1/T), it decreases almost to zero at lower T, it becomes becomes negative below 250 C
ordinary Hall coefficient is negative and large -8E-11 Ohm*m/T(Hall angle=-1.28E-3 1/T), it weakly increases to -12E-11at lower temperature;
Conductivity : 1.602E7(S/m)
hcp structure
Nickel Ni
Transport is hole-dominated
non-ordinary Hall coefficient is big negative Rs=-70E-11 Ohm*m/T (Hall angle=-10.1E-3 1/T), decrease almost to zero at lower T.
ordinary Hall coefficient is negative -4E-11 Ohm*m/T (Hall angle=-0.572E-3 1/T);
Conductivity : 1.43E7(S/m)
Iron-Cobalt Fe- Co (bcc)
non-ordinary Hall coefficient is positive and very large Rs=400E-11 Ohm*m/T, at Co=15%
ordinary Hall coefficient is negative and largest -25E-11 Ohm*m/T, at Co =35 %
Properties of FeCo
the spin polarization is negative for Co and positive for Fe ?? some calculated spin polarizations for FeCo , near 16 % of Co sp polarization changes its signs Fe=56 %; Co(25%) sp=-26%; Co(50%) sp=-67%; Co(75%) sp=-73% Co sp=-80% from book "Materials Design and Synthesis for Desirable Magnetic and Optical Properties By Hao Zhu"
magnetic moment of BCC Co maybe the same as BCC Fe
lattice constant =2.87 A x=0, it is near constant till 20 %, next it reduces to 2.83 A for BCC Co
Chromium
At 290 K the Hall coefficient is independent on magnetic field, but at 4.2 and 77 K, R decreased by a factor of three as the field was increased to 147 kG
Titanium
Ti has cph-structure Hall coefficient is of opposite sign for directions parallel and perpendicular to c- axis Rparallel =4.2-11 Ohm*m/T (electron-dominated) Rperpendicular = -7.7-11 Ohm*m/T
note: All metals of cph structures (Ti,Y,Gd) have significant difference of Hall resistance along and perpendicularly to the c-axis indicating very strong spin-orbit interaction.
Terbium
In the paramagnetic region the values obtained for RO and RS are, respectively, -44E-11Ohm*m/T and -420E-11 Ohm*m/T (very large)
| n-Ge | p-Ge | n-Si | p-Si | n-GaAs | p-GaAs | ||
|---|---|---|---|---|---|---|---|
| mobility (cm2/V/s) | 3900 | 1900 | 1450 | 500 | 8000 | 400 | |
| Hall angle/B (*1E-3 1/T) | 390 | 190 | 145 | 50 | 800 | 40 |
Important facts, which are ignored in the oversimplified classical calculations of the ordinary Hall effect (See details here) :
E.g. in an electrical field, an electron is accelerating and its speed and energy may decrease. However, it can happen only if states of at he higher energy and speed are available. E.g. if electron energy is deep below the Fermi energy and a higher energy states are already well-filled, the the electron cannot be accelerated in an electrical field and cannot increase its speed and energy.
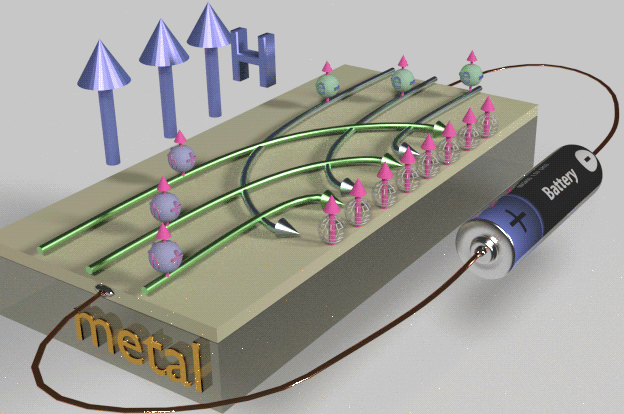 |
The Hall effect in metal. The electron current (green balls) flows from “-” to “+” . In a magnetic field the electrons turn left in respect to direction of their movement. The holes current (blue balls) flows from “+” to “-” . In a magnetic field the holes turn right in respect to direction of their movement. Therefore, at the side of the sample both the spin-polarized holes and electrons are accumulated. it means that at this side of the sample there is no charge accumulation, but there is a large spin accumulation. |
In a metal (also in a semiconductor) the electron and hole are the same object. They are both the negatively- charged electrons. The electrons and holes are distinguished by their energy with respect to the Fermi energy and more specific how their energy distribution (= number of electrons at at a specific energy) changes with an electron energy change. The energy of "electrons" is above Fermi energy and the energy of holes is below the Fermi energy. The number of "electrons" decrease when the electron energy increases. The number of "holes" decreases when the energy increases.
In a metal, the Fermi energy is inside of the electron band and therefore the number of electrons and the holes is nearly equal.
In a semiconductor, the Fermi energy is inside the bandgap and there is a large difference in number of electrons above and below the Fermi energy. In a n-type semiconductor, the Fermi energy is just below the conduction band and there are many "electrons", but there are nearly no "holes". In a p-type semiconductor, the Fermi energy is just above the valence band and there are many "holes", but there are nearly no "electrons".
 Why the electron energy with respect to the Fermi energy defines whether an electron is the "electron" or the "hole"
Why the electron energy with respect to the Fermi energy defines whether an electron is the "electron" or the "hole"
One can distinguish between the "electron" and the "hole" by the direction, into which the electrons move in an electrical field. A negatively-charged particle moves from "-" to "+", but a positively-charged particle moves in the opposite direction from "+" to "-". Even though for both cases of the "electrons" and "holes", a single electron is always accelerated in an electrical field in the same direction from "-" to "+", this acceleration of a single electron courses different direction of the collective movement of the "electron" and "holes".
(where is the magic?) ![]() Why the same direction of movement of a single electron causes different direction of collective movement of many electrons?
Why the same direction of movement of a single electron causes different direction of collective movement of many electrons?
In a solid the conduction electrons move at a high speed in all directions even without an external electrical field. In absence of an external magnetic field, the numbers of electrons, which move in two opposite directions, are exactly equal. E.g. the number of conduction electrons, which move to the left, are the same as the number of the electrons, which move to the right. When an external electrical field is applied, for example, to the left direction, an electron, which moves along the field, accelerates and gains the energy. In contrast, an electron, which moves opposite to the electrical field, slows down and loses its energy. As a result, the electrical field makes an energy shift between the energy distributions for the electrons moving to the left and to the right and therefore the number of the electrons moving to the left and moving to the right, becomes different and therefore there is an electron current along the electrical field. The direction of the current is determined in which direction the left or the right there are more electrons moving.
| Numbers nforward and nbackward of forward- and backward- moving electrons vs. electron energy under an electrical field |
|---|
| Energy distribution of electrons under an electrical field. Right part (blue) shows electrons nforward moving along the electrical field (forward). Left part (green) shows electrons nbackward moving opposite to the electrical field (backward). The total number of electrons moving in each direction is calculated by an integration over all energies. |
| (note): The "electrons" are electrons, which energy is larger than the Fermi energy EF (shown in upper graph). The "holes" are electrons, which energy is smaller than the Fermi energy EF (shown in upper graph). |
| (note): The energy distributions of "electrons" and "holes" describes by the same distribution, the center of which is shifted under an electrical field. |
| (note): The An electron moving along electrical field gains the energy. In contrast, an electron moving opposite to electrical field loses the energy. As a result, the electron distribution of "electrons" and "holes" is shifted towards the electrical field. |
(electron current): More electrons move along the electrical field than opposite to the field (upper graph) |
(hole current): More electrons move opposite to the electrical field than along the field (upper graph) |
| click on image to enlarge it |
In the case of the "electrons" (the electrons, which energy are larger than the Fermi energy), the number of electrons decreases when the electron energy increases. It means that the number of the accelerated electrons, which moves to the left and gain the energy, becomes larger. In contrast, the number of the slowed electrons, which moves to the right and loss their energy, becomes smaller. This imbalance of the electron numbers results in the flow of the electron current to the left.
In the case of the "holes" (the electrons, which energy are smaller than the Fermi energy), the number of electrons increases when the electron energy increases. It means that the number of the accelerated electrons, which moves to the left and gain the energy, becomes smaller. In contrast, the number of the slowed electrons, which moves to the right and loss their energy, becomes smaller. This imbalance of the electron numbers results in the flow of the electron current to the right.
(it is the magic!!!) ![]() (Acceleration of a single electron along an electrical field causes the collective movement of electrons in the opposite direction)
(Acceleration of a single electron along an electrical field causes the collective movement of electrons in the opposite direction) ![]() As explained in above paragraph, the acceleration of electrons in one direction may decrease the decrease of the total number of the electrons, which is moving in this direction (the case of holes) and therefore create an electron current in the opposite direction. It happens due to frequent electron scatterings and redistribution of the electrons according the Fermi- Dirac energy distribution.
As explained in above paragraph, the acceleration of electrons in one direction may decrease the decrease of the total number of the electrons, which is moving in this direction (the case of holes) and therefore create an electron current in the opposite direction. It happens due to frequent electron scatterings and redistribution of the electrons according the Fermi- Dirac energy distribution.
(fact) ![]() The number of electrons, which participate in the electron transport, decreases when the electron energy becomes either larger or smaller than the Fermi energy (See here)
The number of electrons, which participate in the electron transport, decreases when the electron energy becomes either larger or smaller than the Fermi energy (See here)
(fact) ![]() The flow of the electron current in an electrical field occurs not because the electron move faster along the field, but because the number of electrons moving along the electric field becomes larger than the number of the electron moving opposite to the field.
The flow of the electron current in an electrical field occurs not because the electron move faster along the field, but because the number of electrons moving along the electric field becomes larger than the number of the electron moving opposite to the field.
Please see more details about holes and electrons here
![]() (about origin leading to the spin accumulation): The transition from Hall effect due to unpolarized to polarized spin current is confusing.
(about origin leading to the spin accumulation): The transition from Hall effect due to unpolarized to polarized spin current is confusing.
In ferromagnetic metal, both the electrons and holes are spin- polarized. Due to the Ordinary Hall effect the electrons and holes are accumulated at the same side of the ferromagnetic wire. The accumulation of the spin-polarized electrons and holes creates the spin accumulation at a side of a ferromagnetic metal due to the Ordinary Hall effect. it is important that the spin accumulation due to the Ordinary Hall effect is large. It is because the contribution to this type of the spin accumulation from holes and electrons are of the same polarity.
![]() (about application of the effect) The conduction electrons in a ferromagnetic wire are already spin- polarized. Even though the Ordinary Hall effect makes the spin polarization slightly smaller and slightly larger than the equilibrium spin polarization in some places, what difference does it make? In the average the spin polarization is still nearly the same as in the equilibrium?
(about application of the effect) The conduction electrons in a ferromagnetic wire are already spin- polarized. Even though the Ordinary Hall effect makes the spin polarization slightly smaller and slightly larger than the equilibrium spin polarization in some places, what difference does it make? In the average the spin polarization is still nearly the same as in the equilibrium?
(Answer: it creates the pump torque for a spin precession and magnetization reversal) ![]() An increase or a decrease of spin polarization at an interface of a nanomagnet influences the magnetic properties of the nanomagnet such as the Perpendicular Magnetic Anisotropy (PMA) . Also, additional spin polarization increase the magnetic field, which is induced by the spin- polarized electrons (See here). It is important that both changes are created and can modulated by the electrical current. This featured makes possible the parametric enhancement of magnetization precession and the parametric magnetization reversal in a nanomagnet. For parametric magnetization reversal due to modulation of the anisotropy field (see here and here) and due to modulation of the magnetic field, which is induced by the spin polarization, see here.
An increase or a decrease of spin polarization at an interface of a nanomagnet influences the magnetic properties of the nanomagnet such as the Perpendicular Magnetic Anisotropy (PMA) . Also, additional spin polarization increase the magnetic field, which is induced by the spin- polarized electrons (See here). It is important that both changes are created and can modulated by the electrical current. This featured makes possible the parametric enhancement of magnetization precession and the parametric magnetization reversal in a nanomagnet. For parametric magnetization reversal due to modulation of the anisotropy field (see here and here) and due to modulation of the magnetic field, which is induced by the spin polarization, see here.
![]() (about the large magnitude of the spin accumulation) Since the conduction electrons are spin- polarized in a ferromagnet, any electrical current in a ferromagnet is spin-polarized, which includes the Hall current. Therefore, it is very obvious that the Hall creates the spin polarization. What is the new in your findings?
(about the large magnitude of the spin accumulation) Since the conduction electrons are spin- polarized in a ferromagnet, any electrical current in a ferromagnet is spin-polarized, which includes the Hall current. Therefore, it is very obvious that the Hall creates the spin polarization. What is the new in your findings?
The spin accumulation due to the Ordinary Hall effect is not a simple two effects. Both effects the Ordinary Hall effect and the effect of the spin injection (transforming the spin by an electrical current) are very small effect, because they have nearly-equal and opposite contributions from electrons and holes. In contrast, the spin accumulation due to the Ordinary Hall effect is a larger effect, because the polarity of contributions from electrons and holes is the same for this effect
![]() (about height of the hysteresis vs spin accumulation) you mean that from a measure of the Hall effect in a ferromagnet, the efficiency of the spin accumulation can be estimated and the spin accumulation is proportional to the height of the hysteresis loop of the Hall voltage?
(about height of the hysteresis vs spin accumulation) you mean that from a measure of the Hall effect in a ferromagnet, the efficiency of the spin accumulation can be estimated and the spin accumulation is proportional to the height of the hysteresis loop of the Hall voltage?
(Answer 1: about AHE ISHE and OHE)
There are 3 contributions to the Hall voltage in a ferromagnetic metal: (contribution 1: largest) from Anomalous Hall effect (AHE) ; (contribution 2: moderate) from Inverse Spin Hall Effect (ISHE); (contribution 3: smallest) from Ordinary Hall effect (OHE). In contrast to AHE and ISHE, the dependence of Hall voltage is linear for OHE. This property is used to measure OHE in a ferromagnetic metal See here).
Only OHE creates a substantial spin accumulation. The spin accumulation due to AHE and ISHE is much smaller.
For example, in amorphous FeCoB the value of AHE is large ~ 1000 mdeg, the value of ISHE is moderate ~50 mdeg/kG, the value of OHE is close to zero ~0.1 mdeg/kG (see here). The reason for that is that the Fermi sphere in an amorphous material is very simple and very symmetrical. As a result, the density of state is nearly constant at the Fermi energy and there are nearly- precisely- same numbers of holes and electrons.
(Answer 2: about spin accumulation)
Additionally to spin accumulation due to the Ordinary Hall effect, the spin accumulation can be created due to the Spin Hall effect and due to the spin-dependent scatterings across interface.
![]() (compression of spin accumulation due to OHE and the Spin Hall effect) How you can distinguish between the spin accumulation created due to OHE and the Spin Hall effect?
(compression of spin accumulation due to OHE and the Spin Hall effect) How you can distinguish between the spin accumulation created due to OHE and the Spin Hall effect?
The spin direction of spin accumulated electrons due to OHE is the same as the spin direction of spin polarized electrons in an equilibrium (along the magnetization). In contrast, the spin direction of spin accumulated electrons due to the Spin Hall effect generally different the equilibrium spin direction
Case of OHE:
The OHE only redistribute existed spin polarized electrons in a ferromagnetic metal without creating them. As a result, spin direction of spin accumulated and existed spin polarized electrons is exactly the same
Case of the Spin Hall effect.
In this case the spin polarized electrons are created due to the spin dependent scatterings. For example, even in a non-magnetic metal the spin accumulation can be created. The spin direction of created spin accumulation depends on the symmetry of scattering and therefore on the interface geometry and the crystal orientation.
(about evaluation spin injection efficiency from a Hall measurement)
![]() (about height of the hysteresis vs spin injection) Can the efficiency of the spin injection can be estimated from the height of the hysteresis loop of the Hall voltage?
(about height of the hysteresis vs spin injection) Can the efficiency of the spin injection can be estimated from the height of the hysteresis loop of the Hall voltage?
(Answer 1: about AHE ISHE and OHE)
There are 3 contributions to the Hall voltage in a ferromagnetic metal: (contribution 1: largest) from Anomalous Hall effect (AHE) ; (contribution 2: moderate) from Inverse Spin Hall Effect (ISHE); (contribution 3: smallest) from Ordinary Hall effect (OHE). In contrast to AHE and ISHE, the dependence of Hall voltage is linear for OHE. This property is used to measure OHE in a ferromagnetic metal See here).
The efficiency of the spin injection and magnitude of OHE are proportional values, because they both strongly dependent of the imbalance of numbers of holes and electrons in a ferromagnetic metal
For example, in amorphous FeCoB the value of AHE is large ~ 1000 mdeg, the value of ISHE is moderate ~50 mdeg/kG, the value of OHE is close to zero ~0.1 mdeg/kG (see here). It indicates that the spin injection efficiency in FeCoB is very small (close to zero).
The reason for that is that the Fermi sphere in an amorphous material is very simple and very symmetrical. As a result, the density of state is nearly constant at the Fermi energy and there are nearly- precisely- same numbers of holes and electrons.
![]() (about definition of the spin injection) As I understand the spin injection describes the injection of spin- polarized electron due to an electrical current flow from one material to another material, for example, from a ferromagnetic metal to a non-magnetic semiconductor.
(about definition of the spin injection) As I understand the spin injection describes the injection of spin- polarized electron due to an electrical current flow from one material to another material, for example, from a ferromagnetic metal to a non-magnetic semiconductor.
You are correct, the injection of spin polarized electrons from one material to another material due to an electrical current is called the spin injection. However, the spin injection has more wide definition and also describes the spin transfer from one spatial point to another spatial point in one material.
There are two mechanisms for spin transport. The first one is the spin diffusion, which is independent of an electrical current and which describes spin diffusion from a place of a smaller spin accumulation to a place of a larger spin accumulation. The second spin transport mechanism is spin drift by an electrical current or the spin injection. An equilibrium distribution of the spin- polarized electrons is established by the spin diffusion. An electrical current changes this equilibrium by drifting some spins along its flow. For example, the spin diffusion length can be enlarged if an flow along it (See here)
(about influence of standing-wave electrons on the Hall effect due to defects and interfaces)
Due to defects and interfaces, a part of the conduction electrons becomes the standing-wave electrons. As a result, the conduction of metal decreases, but the strength of the Hall effect increases.
![]() (from Szymon Królak) you frequently mention, that there exist two currents: the current of full-filled states, as well as half-filled ones. However, during the explanation of the Hall effect, you state, that the full-filled states form standing waves and therefore do not move. Could you elaborate on that? I am referring to the explanation below, figure 15: The current of "full" states is the normal current. This means that the negatively charged "full" states diffuse from a "-" source toward a "+" drain. Due to the Hall effect, they should turn to the left (similar to the electrons shown in Fig. 14). However, most of the electrons, which occupy the "full" states, are the standing-wave electron. (See Fig.9 here). The standing-wave electrons do not move, therefore they do not contribute to the Hall current
(from Szymon Królak) you frequently mention, that there exist two currents: the current of full-filled states, as well as half-filled ones. However, during the explanation of the Hall effect, you state, that the full-filled states form standing waves and therefore do not move. Could you elaborate on that? I am referring to the explanation below, figure 15: The current of "full" states is the normal current. This means that the negatively charged "full" states diffuse from a "-" source toward a "+" drain. Due to the Hall effect, they should turn to the left (similar to the electrons shown in Fig. 14). However, most of the electrons, which occupy the "full" states, are the standing-wave electron. (See Fig.9 here). The standing-wave electrons do not move, therefore they do not contribute to the Hall current
![]() You are correct.
You are correct.
(about full state and standing- wave electrons): The full state and the sdanding-wave electrons are two different states of an electron. The full state is related to the electron spin and the standing- wave electrons are related to the electron wave vector.
(standing-wave electrons & their influence on the Hall effect)
(What is the electron current?) The electron current does not mean that the electron starts to move in one direction under applied voltage from "-" to "+" potential or the electron speed in this direction is changed. Even in absence of the applied voltage, there are always electrons, which move in both the forward and the backward directions. An electron current means that there are more electrons, which are moving along applied voltage, than electrons, which are moving in the opposite direction.
In absence of the voltage the number of electrons moving in any direction is exactly equal to the number of electrons moving in the opposite direction. The applied voltage makes a number of electrons moving in each direction different. In the direction along the applied voltage the number becomes slightly larger and in the opposite direction the number becomes slightly smaller.
(Origin of the standing wave electrons): Next, just imagine, that there are two defects close to each other inside a metal, which reflects the electron backward as a mirror reflects light. Then, the electron bounces between these two defects forward and backward. Such a bounced electron is a sum of forward and backward-moving electrons with exactly the same amplitude of the wave function. It means that the existence of these two defects firmly fixes the ratio between numbers of forward and backward-moving electrons and the applied voltage does not change this ratio and the numbers of the forward and backward-moving electrons are always equal independently of the applied voltage. Since the applied voltage does not change the ratio between the numbers of the forward- and backward- moving of these electrons, these electrons do not contribute to the electron current. These electrons, I call the standing-wave electrons.
In the above example, I assumed that the reflection of an electron from a defect is 100 %. In reality the reflection is much smaller. It is smaller than 1 %. As a result, only a small part of the conduction electrons are the standing- wave electrons, for which the ratio of is fixed and which do not contribute to the electron current. For other conduction the ratio is not fixed and they do contribute to the electron current.
(an interface as the origin of the standing-wave electrons): A surface or an interface between two metals substantially reflects the conduction electrons. As a result, there are many standing-wave electrons in the proximity of the interface and the conductivity near an interface is smaller than the conductivity in the bulk of the metal. Additionally, the conductivity near an interface is anisotropic, because the reflection of an electron from the interface depends on the electron incident angle.
![]() (Why should we care about the standing- wave electrons and why the standing-wave electrons are important for AHE and ISHE?) The standing- wave electrons do not contribute to electron current, so what? Why we just cannot forget about them? The localized electrons do not contribute to current as well.
(Why should we care about the standing- wave electrons and why the standing-wave electrons are important for AHE and ISHE?) The standing- wave electrons do not contribute to electron current, so what? Why we just cannot forget about them? The localized electrons do not contribute to current as well.
There are two reasons:
The 1st reason is that there is another kind of the electron current, for which an electron just jumps from one spatial position to another. It is a very inefficient current and usually can be ignored, but when the number of standing wave electrons becomes larger, the contribution from this 2nd-type of current can become dominated. This kind of current has a huge AHE. Therefore, when the number of standing-wave electrons becomes larger, the normal current decreases and the 2nd type of current increases, AHE becomes huge. For example, the side-jump scatterings and the spin-dependent scatterings across the interface belong to this 2nd kind of current.
The 2nd reason, why the standing-wave electrons are important for AHE, is that a standing-wave electron effectively couples the conduction and localized electrons.
(localized vs conduction electrons)The localized and the conduction electrons are very different. Their size, symmetry and properties are very different. For example, the spin distributions of localized and conduction electrons are very different. The spins of localized electrons are either parallel or antiparallel to each other. There are 3 groups of conductions electrons with respect to the spin: spin-polarized, spin-unpolarized and spin-inactive conduction electrons (or full state). The different frequency of the scatterings makes the properties of conduction and localized electrons to be so different.
(difference in scattering probability) The scatterings of the conduction electrons are frequent and the scatterings of localized electrons are very rare. The scatterings between localized and conduction electrons are very rare as well, because of the difference in size and symmetry of these different types of electrons. Additionally, a conduction electron moves, a localized electron stays at one place. Therefore, there is a difference in momentum.
The standing-wave electrons have the same symmetry and the same size as the moving conduction electrons, but they stay at the same place. As a result, both types of scatterings between localized and standing- wave electrons and standing- wave and moving conduction electrons are relatively frequent. Overall, the existence of standing-wave electrons makes the probability of scattering between the localized and standing- wave electrons higher.
Since AHE is originated from a spin- dependent scattering of conduction electrons on the localized electrons, the high scattering probability between the conduction and localized electrons makes AHE larger.
(About "full" states or spin-inactive states)
A conduction electron also can be distinguished by its spin. There are 3 different groups of conduction electrons, which are distinguished by the spin.
(group 1) “Full” state or spin- inactive state. It is the case when two electrons occupy one quantum state. The time-inverse-symmetry for this state is not broken. The spin direction of each individual electron cannot be distinguished in this state. As a result, such electrons do not contribute to any spin- related features.
(group 2) Spin- polarized electrons. It is the case when one electron occupies one quantum state and one state remains unoccupied. The spins of all electrons are directed in one direction.
(group3) Spin- unpolarized electrons. It is the case when one electron occupies one quantum state and one state remains unoccupied (similar to group 2). The spins are distributed equally in all directions. Each group has its own distribution of electrons over the electron energy. Since the electron distribution mainly determines features of the electron current, the electron current for each group is very different.
The electrons of each group could be either the standing- wave conduction electrons or “normal” moving conduction electrons.
(increase of standing wave electrons at a lower energy. The hole transport)
![]() (following question from Szymon Królak) Why most full-state electrons are standing-wave electrons? In the explanation above, you stated that a single defect can localize an electron. Are most of the full-state electrons standing-wave electrons because of the fact that at energies lower than the Fermi energy there are a lot of electrons and the Pauli pressure is large? In short: is the effect of a large amount of neighboring full-state electrons similar to a defect, in the sense that it can localize an electron?
(following question from Szymon Królak) Why most full-state electrons are standing-wave electrons? In the explanation above, you stated that a single defect can localize an electron. Are most of the full-state electrons standing-wave electrons because of the fact that at energies lower than the Fermi energy there are a lot of electrons and the Pauli pressure is large? In short: is the effect of a large amount of neighboring full-state electrons similar to a defect, in the sense that it can localize an electron?
![]() You understand the case correctly. Even though the full state is a property of the spin and the standing-wave electrons are a special property of electrons, at an electron energy substantially lower than the Fermi level nearly all electrons are in the full-state or the spin-inactive and are the standing wave electrons.
You understand the case correctly. Even though the full state is a property of the spin and the standing-wave electrons are a special property of electrons, at an electron energy substantially lower than the Fermi level nearly all electrons are in the full-state or the spin-inactive and are the standing wave electrons.
At an energy substantially lower than the Fermi level, almost all states are filled by two electrons and there are only a few, which are filled by one electron and which one space is not filled. The states filled by two electrons are "full" states or spin inactive states. The states filled by one electron are holes.
When there are a few empty states, the scattering of an electron from a "full" state into the empty space becomes rare. For this reason, the life time of the "full" state becomes long (e.g. in comparison to the life time of the "full" state at the Fermi energy) and, consequently, the length of the "full" state (or the same the propagation length between two scatterings) becomes longer. For a longer length the reflection from defects and interfaces becomes more probable and, therefore, there are more standing-wave electrons. It is because one electron covers many defects and interfaces simultaneously.
By the way, the standing-wave electrons are not a "defect" electrons, because an interface is more effective in creation of a standing-wave electron than a defect due to its better reflection of an electron.
(standing-wave electron vs localized electron) The standing-wave electron is not a localized electron. The localized electron is an electron of the size of an atomic orbital of ~0.1 nm. In Fe or Co the localized electron has the d- symmetry. The scatterings of the localized electrons are rare. The standing-wave electron is a conduction electron of a longer size of about 10-100 nm. The symmetry of the standing-wave electron is the symmetry of the conduction electrons (p- or s-). The scattering of the standing-wave electron is frequent.
I will try to answer your questions as soon as possible