Dr. Vadym Zayets
v.zayets(at)gmail.com
My Research and Inventions
click here to see all content |
Dr. Vadym Zayetsv.zayets(at)gmail.com |
|
|
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
|
Orbital moment. Quenching of orbital moment in a solid
Spin and Charge TransportAbstract:(symmetry:) The orbital moment describes the degree of breaking of the rotational symmetry of an elementary particle. The rotational symmetry is more complex than the time- inversion symmetry, which is described by the spin.(magnetic moment:) Since rotational symmetry includes the time-inverse symmetry, an elementary particle has a magnetic moment and interacts with a magnetic field, when it has an orbital moment.(Quenching of orbital moment): The orbital moment of a localized electron in a solid is usually quenched meaning that the orbital moment is zero. The orbital moment is quenched, because the localized electron forms a bonding with a localized electron of a neighbor atom, which fixes the spatial distribution of the localized electron against any rotation or precession. The orbital moment of a conduction electron is usually not quenched.
|
 Breaking/ Unbreaking the time inverse symmetry: 2 cases: spin & orbital moment |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Unbroken time inverse symmetry. Comparison of 2 cases: (case 1) a quantum state is occupied by two electrons of opposite spins and (case 2) a quantum state is occupied by two electrons of opposite orbital moments | |||||||||||||||
|
|||||||||||||||
 (absence of magnetic moment & no interaction with external magnetic field): The time- inverse symmetry is not broken for both quantum states, which are shown at the left and the right sides. As a result, both quantum states do not have a magnetic moment and do not interact with an external magnetic field. The broken time- inverse symmetry is essential for a quantum state to have a magnetic moment (See here). |
|||||||||||||||
| click on image to enlarge it |
Important facts to understand the reason for the quenching of the orbital moment:
(fact 1): 
The orbital moment of a localized electron is usually quenched meaning its orbital moment is zero. In contrast, the orbital moment of a conduction electron is unquenched.
(fact 2): The orbital moment is quenched because of the electron bonding with the neighbor electrons of neighbor atoms in the crystal lattice.
(fact 3): The orbital moment corresponds to a degree of asymmetry of the orbital distribution. It means that the special distribution of an orbital with a non-zero orbital moment is non- spherical and elongated in one or several direction.
(fact 4): When the orbital moment is unquenched, the elongation of the orbital distribution can rotate in any direction according to the direction of the applied magnetic field and, therefore, the elongation direction of the orbital distribution is not fixed by the bonding directions with neighbor atoms.
(fact 5): When an electron is participating in the bonding with a neighbor atom, its orbital moment is quenched. The degree of the participation of in the bonding with a neighbor atom corresponds to the degree of quenching of the orbital moment.
Why is the quenching of orbital moment important?A. When the orbital moment is quenched, the spin from a photon is efficiently transformed into the spin of an electron. This is important to increase efficiency of a high-speed optical memory, in which the magnetization reversal by light is used as a recording mechanism (See here). When the orbital moment is not quenched, the efficiency of the light-to- photon spin conversion is poor.
How to know whether the orbital moment is quenched or not?A. A good sign that the orbital moment is fully quenched is when the g- factor of electron is equal exactly 2 as in the case of a free electron in vacuum. The g-factor could be measured by the Electron Paramagnetic Resonance (EPR), Ferromagnetic resonance (FMR), Magnetic Circular Dichroism (MCD). Some researchers believe that difference of the g-factor from 2 means that the orbital moment is partiality unquenched. It is not correct. The g-factor may be significantly enlarged or be reduced due to the spin-orbit interaction (See here). The spin-orbit interaction is not related to the quenching of the orbital moment.
Why is the orbital moment never quenched in the atomic gas, but is nearly always quenched in a solid?
(fact): In an atomic gas, the orbital moment is never quenched, because each individual atom does not practically interact with other atoms and is almost a closed system. In contrast, the orbital moment of a localized electron in a solid is usually always quenched, because each localized electron makes a strong bonding with neighbor localized electrons.
In the gas the orbit of an atom can be in any direction as well as corresponded orbital moment. Even though the orbital moment of each individual may be non-zero and the time-inverse symmetry is broken for each atoms, for the atomic gas as whole the time-inverse symmetry is not broken, because of the random orientation of the orbitals moments for each atom in the atomic gas.
Orbital moment in Atomic gas |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||
| (fact): Spatial rotation of electron orbital due to a non- zero orbital moment of each electron does not affect any property of an atomic gas (in contrast to a solid, see below) | ||||||||||||
| For clearer understanding the orbitals is depicted as 2D ellipses. | ||||||||||||
| click on image to enlarge it |
(fact): The precession of the orbital moment literally means the precession of electron orbit as well.
| Precession of orbital moment in a magnetic field | ||||
|---|---|---|---|---|
| (fact): The precession of the orbital moment literally means the precession of electron orbit. | ||||
|
||||
| click on image to enlarge it |
(fact): The precession of the orbital moment literally means the precession of electron orbit.
(fact): An electrons in a solid make bonds with neighboring atoms. For this reason, the spatial distribution of the electron orbital is firmly fixed with respect and in direction of the atomic lattice
Quenched and Unquenched orbital moment in the solid |
|||||||||
| Why there can not be a precession of electron orbital and, therefore, orbital moment in a crystal? | |||||||||
| (fact): The precession of the orbital moment literally means the precession of electron orbit. | |||||||||
|
|||||||||
| (localized electrons):It is a feature of the localized electrons, because each localized electron is responsible for one bonding. For this reason, the orbital moment of a localized electron is quenched. | |||||||||
| (conduction electrons): A conduction electron is an exception. Since a large number of conduction electrons contribute to the same bonds. The orbital moment of a single conduction electron can rotate. For this reason, the orbital moment of a conduction electron is unquenched. | |||||||||
| The electron orbitals are shown in pink, nuclei are shown in black. Green arrow shows direction of the orbital moment. Blue arrow shows direction of the magnetic field | |||||||||
| click on image to enlarge it |
(exception): conduction electrons
The contribution of the conduction electrons into the atomic boding is more complex (the metallic bonding). For this reason, the orbital moment of a conduction electron is unquenched (see below).
Why is the orbital moment of localized electrons quenched, but the orbital moment of conduction electrons is not??
The length of a localized electron approximately equals the distance between neighbor atoms in a crystal lattice (~0.1 nm) and, therefore, about the length of the bonding between neighbor atoms . Each localized electron is responsible for one specific atom-atom bonding and that one specific bonding is only on the existence of one specific electron (filling of one specific localized state). As a result, when the orbital moment of this specific localized electron is rotated or is precessing, the strength of the bond is substantially modified. It is the reason why the orbital moment of a localized electron is quenched.
In contrast, the length of a conduction electron is substantially longer (~10-1000 nm). Each conduction electron contributes to many bonding between many atoms. Additionally, millions of other conduction electrons contribute to the same bonding. All those other electrons have all different orbital moments. There is a static distribution of those orbital moments over different angles, which is determined and fixed by the very- frequent scatterings of the conduction electrons. . As a result, when the orbital moment of one specific conduction electron is rotated or is precessing, the distribution of orbital moments of all conduction electrons remains unchanged and, therefore, the rotation and precession do not affect any bond between any atoms.. It is the reason why the orbital moment of a conduction electron is unquenched.
Delocalized conduction electrons.
The orbital moment is
(1) nearly-fully unquenched in a general case
(2) can be partiality quenched in some cases
The effective length of conduction electrons may be over 1000 lattice periods. A million and more conduction electrons are overlapped at each spatial point in a metal. It means that a huge number of conduction electrons contributes to a bonding between each pair of two atoms. A rotation of the orbital moment of one conduction electron does not affect any bonding.
Localized d-electrons.
The orbital moment
(1) nearly-fully quenched in a general case
(2) partially unquenched in some cases
Even though the d-electrons are localized, their size is sufficient to interact with the neighboring d- orbitals. There is a substantial exchange interaction between neighbor d-electrons (See here). The exchange interaction is strong, because there is a substantial overlap of neighboring d- orbitals.
The d- electrons have t and e symmetrical states according to the ligand field theory. The energy separation between d and t state is called the ligand-field splitting parameter delta. Only in the case of a smaller delta, the d-electrons can be in the high spin state. It proves that there is a strong interaction between d-electrons and the lattice. The orbits of the d-electron are fixed by the lattice symmetry and it can not freely rotated. Definitely, the orbital moment of the d-electrons are quenched.
Localized f- electrons.
The orbital moment is either quenched or partially quenched
The f-electrons only weakly interact with f- electrons of neighboring atoms.
Movement of a conduction electron in a metal |
|---|
 |
| Simultaneously with movement along the crystal a conduction electron rotates around each nucleus. |
| For this reason, the effective length of conduction electrons may be over 1000 lattice periods and one conduction electron can simultaneously contribute to the orbitals of many atoms. As the orbital of a conduction electron rotates, the spatial distributions of orbitals of many atoms rotate simultaneously. Since many conduction electrons contribute to the bonding of one atoms, a rotation of the orbital moment of one conduction electron does not affect any bonding. |
Physical mechanisms responsible for quenching of the orbital moment.
(fact) Bonding between atoms makes an electron orbital even more asymmetric, which means the rotation symmetry for the orbital is still broken even in the case of the quenched orbital moment. Therefore, even quenched the orbital moment is non-zero and still exists for the bonded orbital.
If the orbital moment still exists and it is a non- zero, how then does the orbital moment become quenched and inactive?There are two possible mechanism responsible for the quenching of the orbital moment:
(mechanism 1: minor) Bonds between neighboring atoms are formed from equal amounts of the electron orbitals of opposite orbital moment, for example, orbitals with L=+1 and L=-1. A bond couples those two states into one state without the orbital moment.
(note): This condition substantially limits the freedom of the formation of the bond. In fact, the p- symmetry orbitals require a coupling of three orbitals of the same amplitude and a different symmetry to form a bond without any orbital moment. It is a very tough condition. This mechanism may contribute slightly to quenching of the orbital moment, but its contribution is minor.
(mechanism 2: major) There is a magnetic field along bonding, which fixes the orbital moment along one direction and which resists any tilting of the orbital moment by an external magnetic field. This magnetic field is similar to the magnetic field, which holds the spin along the magnetic easy axis.(See here)
When an external field is applied to the force the orbital moment to tilt or to precess, the large internal magnetic field along the bond prevents the orbital moment to do so.
The degree of quenching of the orbital moment is determined by the strength of the internal magnetic field along the bond.
(important fact): The orbital moment and the spin do not interact directly. They both are aligned along the direction of the broken spatial and time-inverse symmetries of the electron orbital. The orbital moment describes the degree of the broken rotational symmetry of the electron orbital. The spin is aligned along the magnetic field of the spin orbit-interaction HSO , which is also directed along the direction of the broken symmetry of the electron orbital. Even though the broken rotation symmetry and the broken orbital symmetry, which creates HSO , are very different, mostly the directions of both broken symmetries are in one direction. As a result, the spin is aligned along the orbital moment, even though there is no direct interaction between the orbital moment and the spin.Approximated Hamiltonian for Spin- orbit interaction |
 |
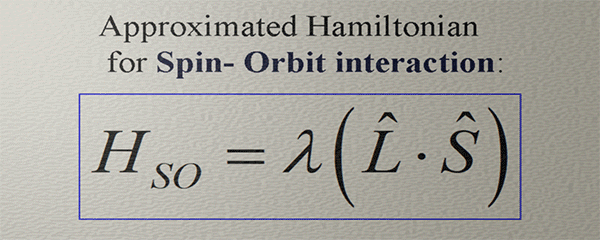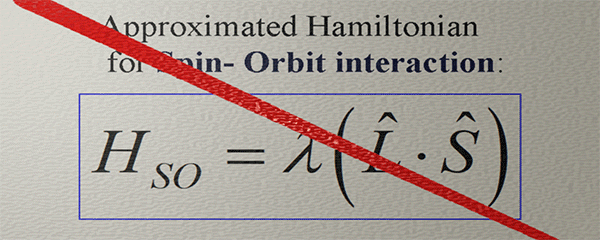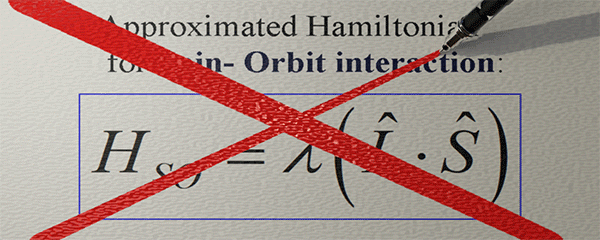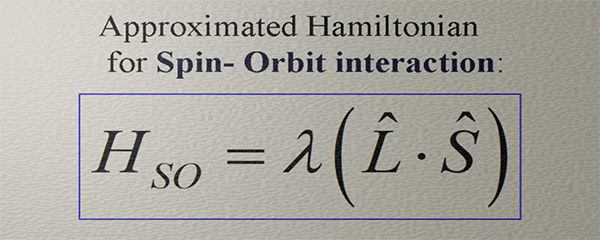| (note) This Hamiltonian captures only a very general tendency that the strength and the direction of the magnetic field of the spin-orbit interaction are similar to the strength and the direction of the spin-orbit interaction. |
| The orbital moment and the magnetic field of the spin-orbit interaction do not interact directly. Instead, they align themselves in accordance with the directional and strength patterns resulting from the broken spatial and time-inverse symmetries of the electron orbital. Consequently, they exhibit similar tendencies in terms of their directions and strengths. |
| (example violation of this Hamiltonian) At an interface, the localized electrons undergo a notably potent spin-orbit interaction (See the perpendicular magnetic anisotropy (PMA)). Despite this strong SO interaction, the orbital moment of these localized electrons are fully quenched. It literally means that their orbital moment is zero. |
| click on image to enlarge it |
(important example 1): Existence of a strong spin- orbit interaction in absence of the orbital moment.
In a solid, the localized electrons at an interface experience the most strongest spin-orbit interaction (See the perpendicular magnetic anisotropy (PMA)). However, the orbital moment of these localized electrons are fully quenched. It literally means that their orbital moment is zero.
(important example 2): Dependence on external magnetic field
There is no spin-orbit interaction in absence of an external or internal magnetic field. An external breaking of the time- inverse symmetry is required in order for the spin-orbit interaction to manifest itself. In contrast, the strength of the orbital moment is independent of the magnetic field.
The alignment of the spin and the orbital moment depends on the frequency of the electron scatterings
(fact 1 about SO): The spin-orbit interaction (SO) describes a magnetic field HSO of a relativistic origin. The spin-orbit interaction is related to the spin or the orbital moment. SO is due to the movement of an electron around the nucleus in the electric field of the nucleus. Still the magnetic field HSO interacts with the electron field. The strength of Hso depends on the degree of spatial asymmetry of the electron orbital. The orbital moment also depends on the degree of spatial asymmetry of the electron orbital. Therefore, there is an indirect relation between the strength of HSO and the orbital moment. Since dependence of HSO and the orbital moment on the orbital spatial asymmetry are very different, the relation between the strength of HSO and the orbital moment is complex (See here). Often the direction of Hso coincides with direction of the orbital moment
(fact 2 about alignment of spin along orbital moment & time
): When an electron is scattered into an empty electron quantum state and its spin is not aligned along HSO (& orbital moment), a spin precession is started and the spin slowly aligns itself along HSO (& orbital moment). Eventually, the spin is aligned along Hso (& orbital moment). It is important that it takes time for full alignment of the spin along Hso and, therefore, along the orbital moment.
(important fact 3 about alignment of spin along orbital moment &frequency of scatterings 
): When the electron scatterings are rare, the electron spin is fully aligned along the orbital moment. When the electron scatterings are frequent, the electron spin is not aligned along the orbital moment. It is because, the spin does not have a sufficient time for alignment along Hso (See previous fact)
An atom in an atomic gas is a very close quantum system with a few available quantum states. It does not interact with atom
(electron scatterings): very rare (nearly absent)
(quenching of the orbital moment): fully unquenched
(alignment of spin & orbital moment) perfectly aligned
Instead of the spin S or the orbital moment L, the total moment J=S+L is more useful quantity characterizing the degree of the time- inverse symmetry breaking in the atomic gas.
An
(electron scatterings): rare & moderate
(quenching of the orbital moment): quenched or fully quenched
(alignment of spin & orbital moment) no alignment, but SO enhancement of external magnetic field
I
An
(electron scatterings): frequent
(quenching of the orbital moment): unquenched
(alignment of spin & orbital moment) no alignment, slight alignment
I
Spin Precession |
 |
| Click on image to enlarge it |
(main definition): The g-factor is a proportionality constant between the magnetic moment of a particle and the degree of the breaking of the time- inverse symmetry for the particle, which characterized by the spin and the orbital moment
(definition by Zeeman energy splitting): The g-factor is a proportionality constant between amount splitting of an electron energy level and the applied magnetic field.
(definition by Larmor frequency): The g-factor is a proportionality constant between the precession frequency of the spin (or/and the orbital moment) and the applied magnetic field.
(definition by FMR frequency): In a ferromagnetic metal, the g-factor is a proportionality constant between frequency of ferromagnetic resonance and the applied magnetic field + internal magnetic field in a ferromagnet (See here).
Even though each definition sounds very different from other definitions, all definitions mean the same subject.
The elecrons of atoms in an atomic gas practically are not scattered. As a result, there is more than enough time for the electron spin to align along the direction of the magnetic field Hso of the spin orbit interaction. The diriction of Hso is along the broken spatial symmetry of the electron orbital. The orbital motal is along the axis of the rotional symmetry of the orbital. In an atom, the axis of the rotational symmetry coincides with the direction of the braken spatial symmetry. Therefore, in an atom the spin and the orbital moment are directed in the same direction.
Since both the spin and the the orbital moment describes some degree of the broken time-inverse and, therefore, both contribute to the orbital magnetic moment. The total degree of the broken time- inverse symmetry is the quantum sum of the contributions due to the spin and the orbital moment.
When the orbital moment is quenched and does not contribute to the magnetic moment of the orbital, the g-factor should be determined only by the spin and, therefore, should equal 2? Is it possible to measure the degree of the quenching of the orbital moment from a difference of the measured g-factor from 2?
Yes, when the orbital moment is quenched, it does contribute to the g-factor. The g-factor still could be different from 2 due to the spin- orbit interaction (See below)
Experimentally measured g-factor of localized electrons 
| material | Fe | Co | ||||||
| g-factor | ||||||||
measurement method |
FMR |
FMR |
||||||
Reference |
Experimentally measured g-factor of conduction electrons
| material | GaAs | InAs | InP | InSb | GaSb | GaN | Si | Au |
| g-factor | -0.3 | -15.3 | 1.48 | -51.31 | -9.1 | 1.95 | 1.9980 | 2.11 |
Reference |
1,5 |
2 |
2 |
2 |
3 |
4 |
6,7 |
8 |
measurement method |
CESR |
CESR |
sigma bond and pi bond is here
When the electron rotates around a nucleus in a free atom of atomic gas, it may have one of several possible rotation symmetries, like the s-, p-, d-, f- symmetries. The electron has a specific energy level corresponding to every specific rotation symmetry. (See classical rotation vs. quantum rotation)
When the atom is placed inside a crystal lattice, the electron forms bonding with neighboring atoms. The bonds modify the rotation symmetry of the electron. The symmetry becomes different from the s-, p-, d-, f- symmetries and similar to the bond symmetry, which is called the sigma- or pi- symmetries.. Correspondingly to the change of the rotational symmetry, the electron energy levels change as well
The field, which forces a change of the rotation symmetry from the free atom symmetry (s-,p-,d-) to the crystal symmetry (sigma-, pi-), is called the Ligand field
(fact) The Ligand field is a feature of only the localized electrons, but is not a feature of the conduction electrons.
(fact) The Ligand field is a feature of electrons with a quenched orbital moment. Also, the existence of the Ligand field is one indications that the orbital moment is quenched.
The d-electrons have t and e symmetrical states according to the ligand field theory. The energy separation between d- and t- state is called the ligand-field splitting parameter delta. Only in the case of a smaller delta, the d-electrons can be in the high spin state. It proves that there is a strong interaction between d-electrons and the lattice. The orbits of the d-electron are fixed by the lattice symmetry and it can not freely rotated. Definitely, the orbital moment of the d-electrons are quenched.
Band structure of a direct band semiconductor |
|
The green ellipses show the orbits of the atoms of the gas. The red arrows show the direction of the corresponded orbital moment of an atom. |
Following explanations are based on the Luttinger Hamiltonian. The Luttinger Hamiltonian assumes that delocalized electrons in a solid have similar orbital moment as the free atoms of an atomic gas. More realistic Hamiltonian is the Luttinger-Kohn Hamiltonian, which is based on the symmetry of wave functions rather than the features of the orbital moment. Despite of some "rough" assumptions, the Luttinger Hamiltonian is still useful for understanding of features of delocalized electrons.
This explanation is based on an assumption that the orbital moment is not "frozen". S,L and J denote the spin, the orbital moment and the total moment. j denotes the projection of the total moment on chosen axis.
Conduction band:
s- symmetry; each electron state can be occupied either by two or one electrons or be not occupied. The orbital moment is zero. The electron orbital is spherical.
Since the orbital is spherical, the conduction electrons should not experience the spin-orbit interaction. It is far from truth. The Bloch function of conduction electrons is not spherical, especially in the case of a compound semiconductor. The spin-orbit interaction can be huge for the conduction electrons. For example, in the case of GaAs the g-factor can be even negative for the conduction electrons.
Valence band:
p-like symmetry; each electron state can be occupied either by two or one electrons or be not occupied. There are 3 different bands: heavy holes, light holes and split-off (SO) band
split-off (SO) band
The total orbital momentum is zero. The electron orbital is spherical. Each electron state can be occupied either by two electrons of opposite spins or by one electron or be not occupied.
The projection of the total moment on chosen axis, the orbital moment and spins of two electrons, which could occupy one electron state can be
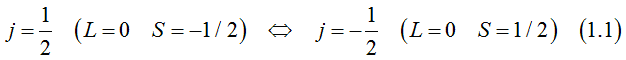
Since the orbital is spherical, the conduction electrons should not experience the spin-orbit interaction. According to the Luttinger-Kohn model the orbitals of electrons of SO band is not spherical.
Heavy-hole band
The total orbital momentum is one. Each electron state can be occupied either by two electrons of opposite spins and opposite orbital moments or by one electron or be not occupied.
Spin is directed along the orbital moment.
The projection of the total moment on chosen axis, the orbital moment and spins of two electrons, which could occupy one electron state can be
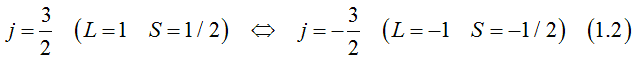
Light-hole band
The total orbital momentum is one. Each electron state can be occupied either by two electrons of opposite spins and opposite orbital moments or by one electron or be not occupied.
The projection of the total moment on chosen axis, the orbital moment and spins of two electrons, which could occupy one electron state can be
Spin is directed opposite to the orbital moment.
The projection of the total moment on chosen axis, the orbital moment and spins of two electrons, which could occupy one electron state can be
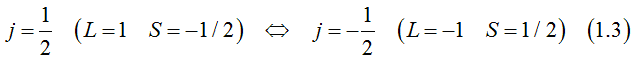
Luttinger Hamiltonian for light and heavy holes
The time-inverse should not change the Hamiltonian. The quantum-mechanical momentum operator p changes sign with time reversal. Therefore, in the Hamiltonian it can be only in a product with other operator, which changes its sign with time reversal. If we assume that there is no any quenching of the orbital moment, due to the LS- coupling (Russell–Saunders coupling) the total moment J should be used as such operator. In the Hamiltonian the time-inverse-symmetrical product 
should be included. In the case of a critical point (band min or max) at p=0, the Hamiltonian should be symmetrical for the reversal of the direction of p, then the product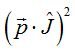 
should be included into the Hamiltonian. The Hamiltonian, which describes both the heavy and light holes bands, should have 4 eigenvalues corresponded to the projections of the total moment -3/2; -1/2;1/2;3/2. Therefore, the Hamiltonian for the heavy and light holes bands can be expressed as
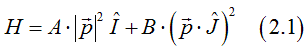
where A and B are constants and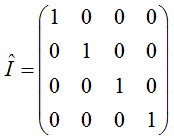 
Along the direction of electron movement (along the direction of p), the projections the total moment can be only -3/2; -1/2;1/2;3/2. Therefore
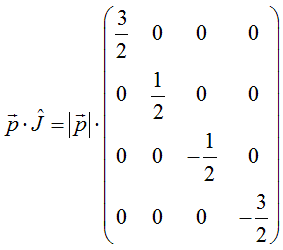and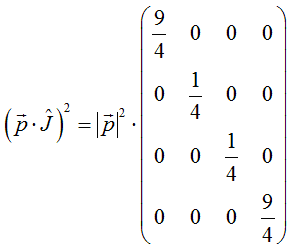 
Solving Eq.(2.1), the energy of heavy holes (j=+/-3/2)can be calculated as
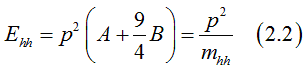
the energy of light holes (j=+/-1/2)can be calculated as
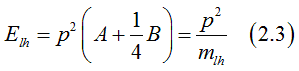
since B<0 , the effective electron mass for heavy holes is larger than for the light holes.
Q. In the case when there is a spin accumulation in the electron gas, is there any accumulation of the orbital moment?
Short answer: Yes. There is an accumulation of the orbital moment.
Long answer:
When there is no spin accumulation and no external field, the time-inverse symmetry is not broken.
There is an equal amount of electrons with opposite direction of the orbital moment.
When there is a spin accumulation in the electron gas, it is always accompanied by an accumulation of the orbital moment. It is because the interaction between the spin and the orbital moment (It is not the spin-orbit interaction!) The accumulation of the orbital moment may be weak. For example, it is weak in the case of electrons of the conduction band in a semiconductor, where the orbital moment of the electrons is nearly zero. Another example of a weak accumulation of the orbital moment is the accumulation in a material with the quenched orbital moment.
Q. The accumulations of the spin and the orbital moments are of the same kind. Is it correct?
Short answer: No. The accumulations of the spins and orbital moment are of different kinds, but often they coexist in the electron gas at the same time.
Long answer
The electron spin in a crystal can be directed in any direction. The special distribution of an electron in a crystal does not change when its spin changes the direction. In the contrast, the orbital moment may have only fixed directions in the crystal. To each direction of the orbital moment, each specific electron distribution corresponds. In a crystal, there is a fixed number of possible different electron distributions and therefore possible direction and value of the orbital moment. The
Questions & Answers(about quenching of orbital moment in an amorphous material)
In my understanding, the d-orbital moment is nearly-fully quenched in a single- or poly-crystalline phase, because the orbital is strongly coupled the bonding which is anisotropic due to crystal structure. Otherwise, the crystal would break itself due to orbital dynamics. In this respect, I assume that it could be possible that the orbital is partially unquenched in an amorphous phase, as you wrote in your web page. I intuitively imagine that an amorphous solid is “soft” in the sense that the orbital may rotate. But I think it would be nice to have another argument to explain why an amorphous crystal is “orbital-active”. Is there any experimental evidence that proved this statement? I’m not an expert on experiments, but I guess it might be possible to measure the orbital moment through the selection rule in the optical excitation. Or, do you know any theory/simulation paper that discusses the orbital quenching effect in amorphous and single/poly crystals?(short answer): The bonds to the close neighbors are the same as in an amorphous material as they are in a crystalline material. Since the bonds to the close neighbors block the orbital rotation and, therefore, quench the orbital moment. The short answer is: The orbital moment is still quenched in the amorphous material.
(possible partial unquenching of the orbital moment in an amorphous material): There is no long-distance order in an amorphous material, it can influence the quenching. It might be similar as in the case of a conduction electron, which is fully unquenched (See here). It only could be the case if the size of the localized electron is longer than the distance between atoms.
(quenching & bonding between neighbor atoms) As you mentioned, the orbital moment is related to the electron wave function and therefore the shape and symmetry of electron orbitals. As a result, in case when the orbital moment changes its direction or there a precession of the orbital moment, the orbital distribution and therefore the bonding is modified. Rotation of the quenched orbital moment will not cause a crystal explosion or or drastic breaking of the bonds between atoms. Nothing, for example, happens when a localized electron is scattered out into gas of the conduction electrons and the state of the localized electron becomes unoccupied.
(unquenching & magnetostriction effect & modification of bonding) When the bonding between neighbor atoms is modified, the distance between atoms changes. When it happens under the influence of a magnetic field, the effect is called the magnetostriction effect. Therefore, any unquenching of the orbital moment should be accompanied by the magnetostriction effect
(about rotation of an electron around a nucleus)
(from Ekta Yadav) "A conduction electron rotates around each nucleus. " Can you give me some reference for this statement?
yes, the electron does rotate around a nucleus. Literally. It is not a rotation when one dot is rotating around another dot. For example, as the Earth is rotating (orbiting) around the Sun. The rotation of an electron around a nucleus is more complex, because the electron is a wave. Nevertheless, it is as a real rotation as any rotation could possibly be.
(Rotation in Quantum mechanics. Rotation & electron orbital) In order to understand it, it is better to start from a 1D structure. Let us look at a wave, which is reflected back and forward between two mirrors. This quantum state is static. It does not move in space.. The field distribution is static as well. However, there are waves, which move forward and backward. Next,Let us look at a similar 2D structure. A wave can move around a circle. In this case, the quantum state has a positive and negative orbital moment for a clockwise and counterclockwise rotation, respectively. Additionally, a quantum state may have zero orbital moment. In this case, the state consists of two waves moving or rotating in the opposite directions. This 2d case is similar to the 1D case of a wave reflecting between mirrors. In the 3D case, the electron rotation can be along any 3D vector (x,y,z). Correspondingly, the direction of the orbital moment can be along any 3D vector (x,y,z).
(Rotation & Orbital symmetry) The fact of rotation of the electron around the nucleus has an even more fundamental origin. In nature, all conserved parameters of an object have corresponding broken symmetries. The spin describes the broken time-inverse symmetry. The rotation (as well as the orbital moment) describes more complex breaking of the symmetry. The rotation means breaking of the space symmetry along with breaking of the time- inverse symmetry. The electron of an atom orbital breaks just this specific symmetry corresponding to the rotation. Meaning that, judging from the most fundamental definition of the rotation, the electron of an atomic orbital is truly rotating around the nucleus.
(Rotation & Bonding between neighbor atoms) The electron rotation or, the same, the electron having a non-zero orbital moment also means that the spatial distribution of the electron wavefunction is changing in time. When an electron state participates in a bonding between atoms, the spatial distribution of the electron wavefunction is fixed, cannot change in time and, therefore, cannot be rotated. For this reason, the electron moment is quenched meaning the orbital moment is zero and there is no electron rotation around the nucleus.
(classical rotation vs. quantum rotation)
(classical rotation) The classical rotation is a 2D type around a fixed axis. (for example, a rotation of a planet around the Sun). The rotation is either circular or elliptical. The direction of the rotation axis may change or there may be a precession of the rotation axis. There is only a single symmetry breaking corresponding to the rotation.
(quantum rotation) The quantum rotation is 3D type (e.g. around a sphere). In contrast to the classical rotation, the quantum rotation can be of a different symmetry. The simplest rotation is around a sphere, which is called the s- type. More complex rotation is of the 8- shape, which is called the p- type. There are even more complex rotations, which are called d- and f- types.
I will try to answer your questions as soon as possible
(condition 1 for a state of rotation symmetry): all states, each which corresponds to a different rotation, should be orthogonal
(condition 2 for a state of rotation symmetry): the sum of all states should give a vacuum state, for which the rotational symmetry is not broken. 
(condition 3 for a state of rotation symmetry): The direction of the broken time- inverse symmetry is the same for all states. It is either along or opposite to one axis for all quantum states of one set. A linear combination of the quantum states gives another set of the quantum state, for which the direction of the broken time- inverse symmetry is different 
