Dr. Vadym Zayets
v.zayets(at)gmail.com
My Research and Inventions
click here to see all content |

Dr. Vadym Zayetsv.zayets(at)gmail.com |
|
 |
more Chapters on this topic:IntroductionScatteringsSpin-polarized/ unpolarized electronsSpin statisticselectron gas in Magnetic FieldFerromagnetic metalsSpin TorqueSpin-Torque CurrentSpin-Transfer TorqueQuantum Nature of SpinQuestions & Answers
more Chapters on this topic:IntroductionScatteringsSpin-polarized/ unpolarized electronsSpin statisticselectron gas in Magnetic FieldFerromagnetic metalsSpin TorqueSpin-Torque CurrentSpin-Transfer TorqueQuantum Nature of SpinQuestions & Answers
more Chapters on this topic:IntroductionScatteringsSpin-polarized/ unpolarized electronsSpin statisticselectron gas in Magnetic FieldFerromagnetic metalsSpin TorqueSpin-Torque CurrentSpin-Transfer TorqueQuantum Nature of SpinQuestions & Answers
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
|
Spin and Charge Transport
Questions & AnswersI truly appreciate all questions. I have tried to answer all of them in details as greater as possibly I can.
|
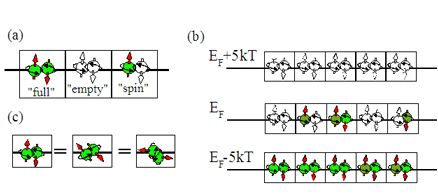 |
Electron states in a solid. Each square represents a delocalized electron state distinguished by a direction of its wavevector k in Brillion zone, its energy E and spacial symmetry. Each state can be occupied maximum by two electrons of opposite spin. (a) Three occupation possibilities of an electron state: a “full” state (spin=0) is a state occupied by two electrons; an ‘’empty” state (spin=0) is a state, which is not occupied by any electrons; a “spin” state (spin=1/2) is a state, in which only one of the two states is occupied. (b) Filling of the states in a metal at different energy. The number of states is described by the density of states. At the energy EF+5kT the states are not filled by any electrons. At the energy EF-5kT almost all states are filled by two electrons of opposite spins and the spin of the states is zero. At the Fermi energy EF a state may be filled only by one electron and have spin ½. (c) Three representations of a “full” state which are undistinguishable. This is because spin of the “full” state is zero and the “full” state does not have a spin direction. Because of this quantum- mechanical property of an electron, electron spin rotates after a spin-independent scattering. |
The energy distribution is the Firmi-Dirac distribution. For states with energies 5kT above the Fermi energy, there is almost no electrons and almost all states are the “empty” states with no spin. For states with energies 5kT below the Fermi energy, almost all states are occupied and almost all states are the “full” states with zero spin. The states with energies near the Fermi energy can be a “full”, “spin” or “empty” or states (occupied by two electrons, one electron or none of electrons).
Let me assume that mobility mu of the electrons in the GaAs is 2800 cm2/V/s. Than, the average time between electrons collision can be estimated as tau_collision= mu* m_eff/q=0.28*0.067*9.1E31/1.6E19 s =10 ps, where m_eff=0.067*m_el is the effective mass of a conduction electron in GaAs and q is the elementary charge.
Let me consider an elastic scattering between 3 states labeled as A, B, C. The energy of states is the same and it is near the Fermi energy. Only the states are distinguished by their direction of the wave vector. For example, the wave vectors of states are directed as
|
||
Fig.2 Two consecutive scattering events, which result in the rotation of a spin direction. After the first scattering at t=10 ps the electron from the state A is scattered into state B. After the second scattering at t=20 ps the electron from the state B is scattered into state C. |
Let me assume that at time t1=0 ps:
At time t2=10 ps the electron of state A is experience an elastic scattering (for example, on defect). During the scattering, electron spin and electron energy do not change. Only the electron wavevector is changed. Since the spin-up place of state B is not occupied, the electron may be scattered into state B. In this case, at time t2=10 ps the state B becomes occupied by two electrons, its spin is zero and it does not have a spin direction.
At time t3=20 ps, one electron of the state B is scattered into state C due a spin-independent elastic scattering. Since there was no electron in state C at time t2=10 ps, the electron scattered into state C may have any spin direction. For example, it may have spin-left direction. Than, spin of the electron, which remains on the state B, is spin-right.
Therefore, the electrons, which had spin-up/down directions at time t1=0 ps, rotates the spin to spin-left/right directions during 20 ps because of two elastic spin-independent scatterings.
The random spin rotation is because of a quantum nature of electrons. At time t2=10 ps, the spin of state B is zero and inside of the electrons there is no record, which spin direction they had at time t1=0 ps. Therefore, when they are scattered out off state B their spin can have any direction, only the spin directions of both electrons should be opposite.
During about a half of all scatterings that an electron experiences, its spin direction is randomly rotates.
If we suggest that spin directions of all electrons are only in spin-up and spin-down directions, within a short time all directions will be mixed and all electrons are redistributed into the TIS assembly (spins are distributed in all directions with equal probabilities). As was shown in the Chapter 8 (Fig. 9), it takes about 15-30 scatterings for two spin directions to be within 1 degree. Therefore, for above example the short time means 150-300 ps.
Q2.The density matrix of the many body state in the classical model gives non-zero probability to measure spin along any direction, not only along a specific one. You should write explicitly the equilibrium many body state in his and the classical model and show that they are different / the same. I am afraid this was not done as it is impossible in the proposed formalism. If I pick a single electron orbital state - which is its entangled TIA or TIS partner? How do I book-keep this with all the scatterings in this model?
A2.
Except the density matrix, the basic wave functions are very important for the description of the spin properties. The basic wave functions can be either spinors or scalars. The description of many body state is different within the classical and proposed models.
In the classical model, the many body state is considered to consist of two-independent states, corresponding to the spin-up and spin-down bands. There is a small interactions between these two states, which is described by a spin relaxation time. Basic wavefunctions of each band are only spinor. There are no scalars. For each spinor wave function of one basic state, there is the orthogonal-spinor wavefunction in other basic set. The density matrix is divided per two. When there is no spin accumulation, there the density matrix is the same for each set. When there is a spin accumulation, the density matrix is different for each set. This corresponds to the basic assumption of classical model of non-interacting spin bands. Each spin band is described by own Fermi-Dirac distribution with different Fermi energy, the transport in each spin band is described by own Ohmic low with conductivity individual for each band and so on.
In the presented model, the many body state is not divided. In the case when there is no spin accumulation (all electrons are in the TIS assembly), the wavefunction of many body state is a scalar. In the case when there is a spin accumulation (there are some electrons in the TIA assembly), the wavefunction of many body state is a spinor of n-rank, where n is the number of electrons in the TIA assembly. The spin relaxation means the decreasing of the rank of this spinor with time, because of a weak interaction of the electron gas with environment.
The TIA assembly describes the number of the basic wave functions, which spinor is the same (their spins are directed in the same direction). The TIS assembly represents all other basic wave functions, which are
scalars, which is a scalar product of two orthogonal spinors
spinors. There is a spinor for any direction of spin. Their production is a scalar.
It is possible to book each electron, which assembly it belongs. Since the spinor of electron is defined, the spin of the electron is defined as well. If the spin of electron is along the spin direction of the TIA assembly, the electron belongs to the TIA assembly. Otherwise, it belong sto the TIS assembly.
At any given time, a number of electrons in the TIS and TIA assemblies and a direction of TIA assembly are measurable parameters and they can be found. Due to the scatterings, there is an exchange of electrons between assemblies. Even an electron can be booked, which assembly it belongs, the electron stays in one assembly only for a short time (1-20 ps).
In contrast, in the classical model an electron stays in each band (spin-up or spin-down) for a long time (~ ms or longer), because the probability of a spin-flip scattering is very low.
I would like to repeat again, that all electrons in the classical model are described only by spinors (There are no scalars). This is not correct.
Q3. You also develop new names of "full" TIA/TIS states for nomenclature with almost 100 years of tradition. "Full" TIA/TIS states are called Triplet/Singlet, I suggest to stick to the standard notation.
A3.
As it can be seen from the example 1, the “Single” and “Triple” terms do not have even slight relation to “full”, “empty” and “spin” states.
About definition of assemblies.
The TIA assembly represents the electrons of a spin accumulation and the TIS electrons with the total spin zero. It is confusing to use in the names of the assemblies the term “spin”. The symmetry of the assemblies for the time reversal is an important property of the assemblies. Why not to use it in the names of the assemblies?
Q4. The density matrix of the many body state in the classical model gives non-zero probability to measure spin along any direction, not only along a specific one.
Q5a. I disagree with this part “within a very short time the spin-independent scatterings will mix up all electrons and there will be electrons with all possible spin directions” I believe that in a magnetic field there is a precession of all spins around the direction of the magnetic field. Only the projections of the magnetic moment can be defined in this case. Because of the Heisenberg uncertainty principle, the spin directions can not be defined. Therefore, the spin directions or the mixing of the spin direction has no meaning in this case.
A4.
An electron does not have a defined spin direction only when it paired with exactly the same electron of the opposite spin ( “full” states, shells of an inert gas, inner shells of atoms and so on).
Otherwise, at any time an electron have a define spin direction. The spin direction is the direction, along which the probability to find the electron with spin parallel to this direction is 1 and to find the electron with spin opposite to this direction is 1. Along any other directions, the probabilities to find electrons along and opposite to that direction are non-zero. (Otherwise, permanent magnets would not exist)
It is true even in case when an electron experiences an interaction (for example, the electron-electron interaction) or the electron spin is not quantum number (for example, the spin precession in magnetic field). It is because the direct relation between the spin direction and the spinor, which describes the electron. See for example here and here
Figure 3 here shows a solution of the Landau–Lifshitz equation for the spin direction, when there is a spin precession around the direction of the magnetic field.
The spin accumulation (or TIA assembly) also has a define spin direction, along which the spins of all electrons of the assembly are directed.
Q5. The probability is not high for the scattering shown in Fig.9, the probability is high for the scattering shown in Fig.10. What does it mean?
A5.
The probability is very low for two neighbor states (only between which a scattering can occur) to have exactly opposite spin directions. Most probable, that spin directions of two neighbor states are neither parallel nor opposite.
The Eqs. (11) and (12a) describes scattering probabilities in such case when two states, have angle phi between their spin direction. The result of the scattering may be either two “spin” states or “empty” +”full” state.
Q6. I conclude that a single scattering event is able to completely change the state of a bulk system with, say, 10^22 particles. (The true meaning is the "single scattering event" - never defined, but used to produce all figures - is most probably something else that the name suggests )
A6.
Even each individual electron experience the spin rotation after each second scattering (each 20 ps in the case of example 1), the many body state does not change. For example, let me in example 1 assume that there is no spin accumulation (all electrons in the TIS assembly). At time t1= 10 ps the spins of electrons are in all direction with equal probability. At time t=30 ps, a half of electrons are experiences a random spin rotation. Since the spin rotation is random, a time t=30 ps still the spins of electrons are in all direction with equal probability. Therefore, nothing is changed for 20 ps. The many body state at t=30 ps is exactly the same as it was at time t=0 ps.
About the definition of the scatterings, I am not sure that I fully understand your question and concern. In the case of GaAs of the example 1, an electron experience a scattering in average each 10 ps (elastic and non-elastic, on defect, on dislocations, on phonons, on magnons and so on).
Q7. An equilibrium spin polarization by a uniform magnetic field depends on the electron spin lifetime, that is a non-equilibrium quantity. This would imply to me, that for a model of non-interacting Fermi electrons, the susceptibility is infinite.
A7.
In an imaginary case when there is no spin relaxation mechanism in an electron gas (spin life time is infinitely long), in the magnetic field the spin polarization of an electron gas is near 100 %. In the magnetic field the spins of electrons precess. Due the Hilbert damping, the spin of electrons aligns along magnetic field (A state with lowest energy). See for example Fig.4 here
The electrons minimize their energy by aligning their spin along the magnetic field. I think it makes a perfect sense.
Q8. Are there any differences in the description of the spin-transfer torque between the classical and your models?
A8.
Yes, there are significant differences. In fact it is very difficult to explain the origin of the spin-transfer torque from the classical model of the spin-up/spin-down bands. The description from the presented model is straightforward.
The origin of the spin-transfer torque as understood from the classical model.
It was clear for the long time that spin-transfer torque occurs because the magnetic moment is transformed from one ferromagnetic metal to another ferromagnetic metal by an electrical current. It was not clear why and how.
It was known that the drift electron current in a ferromagnetic metal is spin-polarized (Click here). Therefore, the spins may be accumulated at interface between metals and next diffuse inside the metals. Within the classical theory it causes the spin accumulation (it makes a larger amount of spin-up or spin-down electrons). That spin accumulation decays with time, because of the spin relaxation. From this classical description of this system it is unclear where the spin-torque is originated. There are some suggestions that it comes from spin relaxation, but at presented all known spin relaxation mechanisms do not cause any spin-torque. Only rough description of the spin transfer torque can be done within classical theory (Click here).
The origin of the spin-transfer torque as understood from the classical model.
In contrast, within the presented theory the origin of the spin-transfer torque is clear. The spin, which diffuses into the ferromagnetic metal, has a different spin direction from the spin direction of existed electrons. The interaction of electrons of different spin directions results of a single spin direction, which is different from a spin direction of local d-electrons. The exchange interaction between the d-electrons and the conduction electrons causes the spin-transfer torque.
In fact, the physics of this effect is even richer
Q9. The spin-transfer current. What it is? Is it a spin current? Is there any other paper, which describes the spin-torque current?
A9.
It was known for a long time that a spin current flows from regions of high spin accumulation to the regions of low spin accumulation. The conventional spin current is an electron current from a region of larger spin accumulation into a region of smaller spin accumulation.
The spin-torque current is a spin current flowing between regions of different directions of spin accumulation. Therefore, it is different from the conventional spin current.
It is possible to imagine how the spin-current flows even within the classical model. See for example here. (please, click to expand the description).
but a numerical description of the properties of this current practically is impossible in the classical model.
However, within the presented model the description of the spin-torque current is straightforward. See here
The properties of the spin-torque current can be understood, numerically described and studied.
Q10. The basic message as of the (in)validity of the "classical model" which this work is supposed to replace is different on different places. You compare the classical and presented models differently? You deliver a feeling that the classical model is wrong as its assumptions are not fulfilled. Also, it is said that the "proposed model gives a different energy distribution than the classical model". It is said that the classical model is significantly limited. It is said that the basic assumption of the classical model … is incorrect. Though, after all of this, the proposed model is declared "… not in contradiction" to the classical model. So are these two models equivalent? If yes, the presented model is irrelevant, as it does not offer any advantage over the classical model. If no, there should be an explicit prediction of a physical result, where these two models differ and the presented model should be demonstrated to be the correct one.
Q10a. You claim that the classical model of the electron gas in a solid is not correct. Since the classical model was established a long time ago, why the incorrectness of the classical theory has not been noticed earlier?
A10.
The starting assumptions for both models are very different. The classical model is based on the assumption that electrons have spins only in two opposite directions (See for example, Kittel C. Introduction to solid state physics (7ed., Wiley, 1996) page 435, Fig.10 or Fig.3 here ). In contrast, the presented model shows that this is incorrect assumption.
However, the classical and presented theory gives similar results in the most of the cases. Only details are different. However, these details are of great importance. That is the reason why I wrote that the presented model can be considered as an extension of the classical model. Also, that is reason why the classical model gives the correct predictions or close-to-correct predictions in most of the cases.
The predictions by the two models are similar in the case when the predicted effect depends only on the spin projection. When the spin direction is important, the advantages of the proposed model are clear and the incorrectness of the classical model is prominent.
Examples when the classical model gives incorrect prediction or the description by the classical model has significant limitations:
Q11. Comments
1. Polarization of photons IS their spin (=1) with the same features as spin of electrons.
2. You can not treat filled and empty states as identical - they can be distinguished by measuring their electric field . Example - Cooper pairs in superconductors are well established physical objects.
3. Time reversal - what you describe is just Kramers degeneracy.
Quantum mechanics of spin and in general is quite rigid , i don't think you can change anything without running a contradiction.
A11.
I agree
Q12.
1. Is any experimental proof that a magnetic field induces a spin accumulation even in a non-magnetic metal like Al or Au? And electrical current in these metals became spin-polarized?
A12.
Even according to the classical theory a magnetic field induces a spin accumulation in non-magnetic metals. The effect is called the Pauli paramagnetism. However, the kind of the spin accumulation induced by a magnetic field is different from the kind of a spin accumulation, which may be injected into the metal from a ferromagnetic metal. In the case of the first kind of the spin accumulation the Fermi energy is the same for spin-up and spin-down bands. In the case of the second kind of the spin accumulation the Fermi energies are different for spin-up and spin-down bands. Allowing such two kind of spin accumulations is one of contradictions of the classical theory.
In the presented theory, the spin accumulations, which is induced by a magnetic field and which is injected from a ferromagnetic metal, are the same and undistinguishable.
Yes, in a magnetic field a drift current in Al and Au is spin-polarized.
Existence of a spin polarization of electronic gas in ferromagnetic metals like Fe, Co and Ni can be considered as an experimental proof. The spin accumulation in this case is because of the effective magnetic field due to the exchange interaction between local d-electron and conduction sp-electrons.
I will try to answer your questions as soon as possible