Dr. Vadym Zayets
v.zayets(at)gmail.com
My Research and Inventions
click here to see all content |

Dr. Vadym Zayetsv.zayets(at)gmail.com |
|
 |
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
|
Perpendicular magnetic anisotropy (PMA) Spin and Charge TransportAbstract:The equilibrium magnetization of a ferromagnetic film is in-plane, because of the demagnetization field. Due to the demagnetization field, the magnetic energy is smaller when the magnetization direction is in-plane than perpendicular- to- plane. However, at an interface an electron may have an additional magnetic energy due to the spin-orbit interaction. This additional energy may be substantial and it makes the total magnetic energy smaller in the perpendicular-to-plane direction. As a result, the direction of the equilibrium magnetization becomes perpendicular-to-plane. This effect is called the perpendicular magnetic anisotropy (PMA).The spin-orbit interaction and consequently the PMA becomes strong only when the electron orbital becomes asymmetric (deformed) in one direction. When the orbital deformation is due to the breaking periodicity at an interface, the effect is called the interfacial PMA. When the orbital deformation is due to the crystal spacial asymmetry, the effect is called the bulk PMA.
|
Mathematics of Magnetic Anisotropy |
|---|
| Anisotropy field is the main parameter describing the strength of magnetic anisotropy |
| click on image to enlarge it |
![]() Main Calculations:
Main Calculations:![]() Calculation of perpendicular magnetic anisotropy (PMA). PMA under bias magnetic field. Magnetization tilt under additional in-plane magnetic field
Calculation of perpendicular magnetic anisotropy (PMA). PMA under bias magnetic field. Magnetization tilt under additional in-plane magnetic field
![]() Calculation of in-plane magnetic anisotropy.
Calculation of in-plane magnetic anisotropy. ![]() Calculation of teh anisotropy field with and without a bias magnetic field. Calculation
Calculation of teh anisotropy field with and without a bias magnetic field. Calculation
![]() (old, but not obsolete)
(old, but not obsolete) ![]() Calculation of perpendicular magnetic anisotropy (PMA) and in-plane anistropy). It also includes calculations of the magnetic energy and thickness dependence
Calculation of perpendicular magnetic anisotropy (PMA) and in-plane anistropy). It also includes calculations of the magnetic energy and thickness dependence
![]() (old, but not obsolete)
(old, but not obsolete) ![]() Calculation of internal magnetic field for a ferromagnetic film having PMA. It also includes calculations under magnetization tilting out of the easy axis
Calculation of internal magnetic field for a ferromagnetic film having PMA. It also includes calculations under magnetization tilting out of the easy axis
![]() (old, but not obsolete)
(old, but not obsolete) ![]() Calculation of internal magnetic field for a ferromagnetic film having the in-plane anisotropy. It also includes calculations under magnetization tilting out of the easy axis
Calculation of internal magnetic field for a ferromagnetic film having the in-plane anisotropy. It also includes calculations under magnetization tilting out of the easy axis
![]() (old, but not obsolete)
(old, but not obsolete) ![]() Calculation of perpendicular magnetic anisotropy (PMA) using the classical Neel model. It also includes
Calculation of perpendicular magnetic anisotropy (PMA) using the classical Neel model. It also includes
| Measurement of strength of Perpendicular Magnetic Anisotropy (PMA) |
|---|
 |
| (measurement the strength of PMA) |
| ( Hani as a measure of PMA energy) |
| (additional measurement: measurement of SOT effect) |
Note. I have developed this measurement method in 2019-2020 |
| click on image to enlarge it |
A. The spin-orbit interaction
(fact) ![]() The PMA or the spin-orbit interaction can be originated either at a nanomagnet interface or in the bulk of the nanomagnet. The interface-originated PMA is stronger and more interesting, because engineering of only the one atomic layer at interface, a huge PMA and unique properties can be achieved.
The PMA or the spin-orbit interaction can be originated either at a nanomagnet interface or in the bulk of the nanomagnet. The interface-originated PMA is stronger and more interesting, because engineering of only the one atomic layer at interface, a huge PMA and unique properties can be achieved.
A. It is because a huge energy is accumulated in only one atomic layer at interface. This allows to fabricated experimentally small nano- sized devices with an unique functionality.
![]() When the volume of an object is reduced, the object energy reduces proportionally to the volume. In order for the object to function as a device (a memory cell, a sensor cell etc), the magnetic energy between its two stable states should be sufficiently larger than the thermal energy kT. Otherwise, it will be continued random thermal switching between two states and the object cannot function as a device.
When the volume of an object is reduced, the object energy reduces proportionally to the volume. In order for the object to function as a device (a memory cell, a sensor cell etc), the magnetic energy between its two stable states should be sufficiently larger than the thermal energy kT. Otherwise, it will be continued random thermal switching between two states and the object cannot function as a device.

The SO by itself cannot break the time inverse symmetry and, therefore, to manifest itself. The HSO exists only when there is an external magnetic field.
When atomic orbital is deformed, the electron becomes closer to the atomic nucleus, where the electrical field is much stronger. As a result, the SO becomes larger.
Key properties of the spin-orbit interaction, which lead to the existence of PMA |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
(key property 1): |
|||||||||||||||
|
|||||||||||||||
| The green arrows show the direction of the effective magnetic field of the spin-orbit interaction HSO The red arrows show the direction the Lorentz force. The blue arrow shows direction of the external magnetic field Hext. | |||||||||||||||
click on image to enlarge it |
|||||||||||||||
(key property 2): |
|||||||||||||||
|
|||||||||||||||
| (note: simplified schematic): the figures shown above are simplified schematic representation of the electron orbital aiming to demonstrate the operation principle of the effect. | |||||||||||||||
| (note about PMA) In the case of the Perpendicular Magnetic Anisotropy (PMA) is only important how the HSO changes under applied magnetic field, but not the absolute value of. At parts closer to nucleus the influence of the the Lorentz force FLor may be weaker. Therefore, for the PMA a complex consideration on an increase of HSO and on a possible decrease of FLor should be considered to analyze the deformed orbital. | |||||||||||||||
| (note about atomic neighbors) In the case of a crystal, a deformation of the orbital and its influence on the HSO depend on neighbor atoms. Proximity of a neighbor can either push out or pull closer the electron orbital to the atomic nucleus. It can influence both the HSO and the orbital deformation due to the Lorentz force FLor. | |||||||||||||||
| (note interface and bulk) at an interface the neighborhood of the atom is different from that of the bulk and the orbital reconstruction (deformation) always occurs at the interface. As a result, the HSO and, therefore, the PMA is very different for the interface and the bulk of the material. | |||||||||||||||
| click on image to enlarge it |

 Hard disk
Hard diskIn order to memorize a huge amount of data onto a small surface of the hard disk, the surface area of one bit is very small ~10 nm x10 nm. Only the SO is able to hold magnetic date in such a tiny area.
(uniqueness of PMA):  There is no known effect except PMA, which allows to store magnetic data in area of 10 nm x10 nm, protecting data from the unwanted thermal switching
There is no known effect except PMA, which allows to store magnetic data in area of 10 nm x10 nm, protecting data from the unwanted thermal switching
 Magnetic random access memory (MRAM)
Magnetic random access memory (MRAM)![]() In MRAM, one bit of data is memorized by two stable magnetization of the nanomagnet. In order to compete with other memory schemes (e.g. DRAM), the volume of nanomagnet should be smaller than ~30 nm x 30 nm x 1 nm
In MRAM, one bit of data is memorized by two stable magnetization of the nanomagnet. In order to compete with other memory schemes (e.g. DRAM), the volume of nanomagnet should be smaller than ~30 nm x 30 nm x 1 nm
(uniqueness of PMA):  There is no known effect except PMA, which allows to store magnetic data in volume of 30 nm x 30 nm x 1 nm, protecting data from the unwanted thermal switching
There is no known effect except PMA, which allows to store magnetic data in volume of 30 nm x 30 nm x 1 nm, protecting data from the unwanted thermal switching
 Molecular recognition sensor
Molecular recognition sensor In the molecular recognition sensor, a surface touching event by a molecule or an virus is detected by a measure of a change of spin-orbit interaction the at the sensor interface. In order to practical the detection area of the sensor should be comparable with the size of the molecule or virus. The practical size is ~30 nm x30 nm. See more details here.
In the molecular recognition sensor, a surface touching event by a molecule or an virus is detected by a measure of a change of spin-orbit interaction the at the sensor interface. In order to practical the detection area of the sensor should be comparable with the size of the molecule or virus. The practical size is ~30 nm x30 nm. See more details here.
(uniqueness of PMA):  There is no known effect except PMA, which allows to store magnetic data in the area of ~30 nm x30 nm protecting data from the unwanted thermal switching.
There is no known effect except PMA, which allows to store magnetic data in the area of ~30 nm x30 nm protecting data from the unwanted thermal switching.
 Nano-sized microwave generator
Nano-sized microwave generatorIn this device the microwave is generated by a stable magnetization precession in a nanomagnet. The A stable single-domain magnetization oscillation can be achieved in a nanomagnet of the volume ~300 nm x 300 nm x 1 nm
(usefulness of PMA): Even though the stable magnetization oscillation can be achieved in a nanomagnet without PMA, the microwave generator made of a nanomagnet with PMA is more reliable and stable.
 Nano-sized magnetic sensor
Nano-sized magnetic sensorA nanomagnet as a part of a tunnel magnetic junction (MTJ) can be used as a nano sensor of a magnetic field. The spatial resolution of the sensor is better for a smaller size of the nanomagnet.
 Energy or
Energy or
Magnetic anisotropy in a Fe film |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
thickness dependence |
||||||||||
|
||||||||||
Magnetic anisotropy in a Fe film depends on its thickness. |
![]() The PMA describes the magnetic field HPMA=HSO- Hdemag, which is a sum of demagnetization magnetic field Hdemag and the magnetic field of spin orbit interaction HSO. In the case of a PMA sample, the direction of HSO is along magnetization M, the Hdemag is always opposite to the M and HSO>Hdemag. As a result, HPMA>0 and M ( the total spin of localized electrons (magnetic moment)) is aligned along HPMA. and perpendicularly to the film surface.
The PMA describes the magnetic field HPMA=HSO- Hdemag, which is a sum of demagnetization magnetic field Hdemag and the magnetic field of spin orbit interaction HSO. In the case of a PMA sample, the direction of HSO is along magnetization M, the Hdemag is always opposite to the M and HSO>Hdemag. As a result, HPMA>0 and M ( the total spin of localized electrons (magnetic moment)) is aligned along HPMA. and perpendicularly to the film surface.
The PMA energy EPMA is the product of HPMA and M (magnetic energy of localized electrons).
![]() In some cases it is preferable to use the PMA energy EPMA instead of the magnetic field HPMA. An example is the thermally- activated magnetization reversal, when the magnetization reversal occurs when the energy of a thermal fluctuation is larger than EPMA.
In some cases it is preferable to use the PMA energy EPMA instead of the magnetic field HPMA. An example is the thermally- activated magnetization reversal, when the magnetization reversal occurs when the energy of a thermal fluctuation is larger than EPMA.
![]() In some cases it is preferable to use the magnetic field HPMA instead of the PMA energy EPMA . An example is calculation of a torque in external magnetic field Hext, when the magnetization procession M occurs around the field, which is the vector sum of Hext and HPMA.
In some cases it is preferable to use the magnetic field HPMA instead of the PMA energy EPMA . An example is calculation of a torque in external magnetic field Hext, when the magnetization procession M occurs around the field, which is the vector sum of Hext and HPMA.
The PMA energy EPMA is defined as a difference between magnetic energies for the cases when when the magnetization is perpendicular-to-plane and in-plane
The difference of HPMA is because of difference of the orbital symmetry. The orbital symmetry at interface is substantially different that in the bulk because of a surface reconstruction at interface and the asymmetry of interaction with atoms from below and above for the interface atoms.
Example:
Fe film: at interface -> HSO>Hdemag, but in the bulk HSO< Hdemag. As a result, equilibrium magnetization of a thinner Fe film is perpendicular- to - film- plane and of a thicker film is in- plane (see here or here).
FeTbB film: in the bulk HSO< Hdemag. Equilibrium magnetization of a thicker FeTbB film is perpendicular- to - plane
Averaging over film thickness
The measured parameters of the PMA magnetic field HPMA and PMA energy EPMA


where t is the film thickness

(direction- dependence of Hdemag) ![]() The demagnetization magnetic field Hdemag is always directed perpendicularly to film surface and opposite to the magnetization direction. Its magnitude is proportional to the perpendicular-to plane component of the magnetization.
The demagnetization magnetic field Hdemag is always directed perpendicularly to film surface and opposite to the magnetization direction. Its magnitude is proportional to the perpendicular-to plane component of the magnetization.
(direction- dependence of HSO) ![]() The magnetic field os spin- orbit interaction HSO is directed along to the magnetization direction (along the magnetic field applied to the atomic orbital). Its magnitude depends on the orbital symmetry (or degree of orbital deformation). Usually atomic orbital is deformed along the film normal. As a result, the HSO may be substantially larger when magnetization M is perpendicular to the film surface in comparison to the case when the magnetization is in the plane.
The magnetic field os spin- orbit interaction HSO is directed along to the magnetization direction (along the magnetic field applied to the atomic orbital). Its magnitude depends on the orbital symmetry (or degree of orbital deformation). Usually atomic orbital is deformed along the film normal. As a result, the HSO may be substantially larger when magnetization M is perpendicular to the film surface in comparison to the case when the magnetization is in the plane.
There is a discontinuity at the film interface. As a result, atomic orbitals are deformed at the interface. Since the effective magnetic field of spin-orbit interaction HSO. depends on the orbital deformation (See SO interaction), HSO becomes larger when the magnetization is perpendicular-to-plane and HSO becomes smaller when the magnetization is in-plane. Correspondingly, the magnetic energy becomes different for the perpendicular-to-plane and in-plane magnetization directions.
The energy of the spin-orbit interaction of only one interface layer may be huge and it may substantially exceed the total magnetic energy of all other electrons in a ferromagnetic film. This large energy of the spin-orbit interaction is used to store a data in small volume of magnetic medium (e.g. a nanomagnet of a MRAM cell, a magnetic domain of a hard disk). Since the electron orbital at the top of a ferromagnetic metal are deformed in the direction of the interface, the energy of spin-orbit interaction is largest for the film with the PMA ( the direction of the equilibrium magnetization is perpendicular-to-plane).
Origin of PMA |
|||
|---|---|---|---|
| Spin-orbit interaction due to the orbital deformation | |||
|
|||
Fig.1. The effective magnetic field of spin-orbit interaction HSO. The depends on the degree of the orbital deformation and the deformation direction with respect of the applied external magnetic field Hext. (a) spherical orbital HSO=0. (b) deformed orbital and an external magnetic field Hext is applied along the deformation. HSO ≠0. (c) deformed orbital and an external magnetic field Hext is applied perpendicularly to the deformation. HSO =0. The electron magnetic energy is larger in the case (b) and smaller in cases (a) and (c) |
|||
| for more details, see here |
In a magnetic media the data are stored by means of two opposite equilibrium magnetization directions. The energy of barrier between these two equilibrium states should be substantially (at least 20-50 times) larger than the thermal energy kT. Otherwise, the magnetization can be thermally switched and the date can be lost (See thermally-activated magnetization switching). The barrier energy is linearly proportional to the volume of the storage cell. In order to make the storage cell smaller, the barrier and consequently the magnetic energy should be larger.
![]() At the interface the electron orbital is substantially deformed towards the interface. Due to this deformation, the spin-orbit interaction is significantly enhanced. This means that there is a large effective magnetic field of the spin-orbit interaction HSO, when the magnetization is along the deformation (perpendicular-to-interface). However, there is no such field, when magnetization is in-plane. The magnetic field HSO may become larger than demagnetization field and the negative magnetic energy become smaller for perpendicular direction than for the in-plane direction. As a result, the perpendicular-to-plane direction of the magnetization becomes energetically favorable.
At the interface the electron orbital is substantially deformed towards the interface. Due to this deformation, the spin-orbit interaction is significantly enhanced. This means that there is a large effective magnetic field of the spin-orbit interaction HSO, when the magnetization is along the deformation (perpendicular-to-interface). However, there is no such field, when magnetization is in-plane. The magnetic field HSO may become larger than demagnetization field and the negative magnetic energy become smaller for perpendicular direction than for the in-plane direction. As a result, the perpendicular-to-plane direction of the magnetization becomes energetically favorable.
The anisotropy field is used to measure the strength of the PMA. The larger the anisotropy field is, the stronger the PMA is.
Two factors are factors are important to understand the equilibrium magnetization direction of a ferromagnetic film: (1) the directional dependence of the spin-orbit interaction; (2) the orbital deformation at an interface
 Model of perpendicular magnetic anisotropy. oversimplified Neel description
Model of perpendicular magnetic anisotropy. oversimplified Neel description
In this model, the total magnetic energy, which is a sum of the energy of the magnetic anisotropy EPMA and the magnetic dipole energy can be calculated as
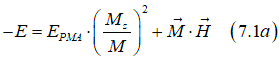
in which the energy of the magnetic anisotropy is assumed to be proportional to a square of the magnetic component Mz along the easy axis.
![]()
where θ is the angle between the magnetization M and the film normal, φ is the angle between the magnetic field H and the film normal
 Model of perpendicular magnetic anisotropy. full description based on properties of the spin-orbit interaction
Model of perpendicular magnetic anisotropy. full description based on properties of the spin-orbit interaction 
The sum of the magnetic energy due to the magnetic field of the spin, the demagnetization field, the magnetic field of the spin-orbit interaction and demagnetization field gives the total magnetic energy as
![]()
where kso is the coefficient of the spin-orbit interaction and kdemag is the demagnetization coefficient
 Comparison of the oversimplified Neel description and full description of PMA
Comparison of the oversimplified Neel description and full description of PMA
| Neel model | full model | note | ||||
|---|---|---|---|---|---|---|
| energy | 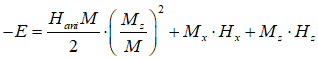 |
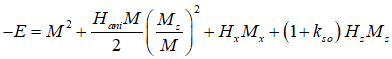 |
the same when kso=0 | |||
| Mx vs Hx |  |
 |
linear,the same as experimentally observed | |||
| anisotropy field | 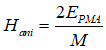 |
|||||
| Hani vs Hz | 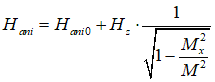 |
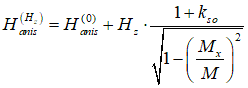 |
the same when kso=0. The dependence is used to measure kso | |||
| energy barrier | 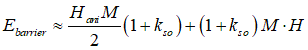 |
the same when kso=0. used in the classical model of magnetization reversal (See here) | ||||
Mathematics of Magnetic Anisotropy |
|---|
| Anisotropy field is the main parameter describing the strength of magnetic anisotropy |
| click on image to enlarge it |
The Einstein theory of relativity states that an electron moving in a static electric field experiences an effective magnetic field, which is called the effective magnetic field of the spin-orbit (SO) interaction HSO .The electric field of atomic nucleus may induce a substantial HSO, because the electron moves with a very high speed on its atomic orbital in close proximity to the atomic nucleus. However, the value of the HSO substantially depends on the orbital symmetry. It is because the electron experiences different directions of the HSO on different parts of the orbit that may compensate each other. For example, in the case of a spherical orbital the contributions to the HSO are equal and opposite in sign and the resulting HSO=0. In the case of a deformed orbital, when the orbital is elliptical or/and the orbital center is shifted from the nucleus position, the HSO becomes substantial and proportional to the degree of the orbital deformation. Also, the HSO is linearly proportional to an external magnetic field Hext. Figure 1 demonstrates how the HSO changes depending on the direction of the orbital deformation and the direction of the external magnetic field. When the orbital is spherical (Fig.1a), the HSO equals to zero independently on the direction of the Hext. When the orbital is deformed and the Hext is applied perpendicularly the orbital deformation (see Fig.1b), the HSO is also zero, because the orbital is symmetrical along the direction of the Hext. For the cases of Figs. 1a and 1b, the magnetic energy of the electron Emag is equal to:
![]()
where S is the electron spin and is mB the Bohr magneton. When the orbital is deformed and the Hext applied along the orbital deformation (Fig.1c), the HSO becomes a non‐zero and proportional to the Hext. In this case the Emag equals to:
![]()
The absolute value of the electron magnetic energy is larger in the case shown in the Fig. 1c and smaller in the cases shown in the Figs. 1a and 1b. Therefore, the orbital deformation substantially changes the electron magnetic energy and therefore magnetic properties of the ferromagnetic film.
The equilibrium magnetization of an isotropic ferromagnetic thin film can be either in‐plane or perpendicular‐to‐plane depending on the deformation of the electron orbitals at the film interface and the thickness of the film. The interaction of analyte molecules with interface electrons of the ferromagnetic film leads to the orbital deformation of the interface electrons and consequently to a change of the PMA. Consequently, the change of magnetization direction of the ferromagnetic film due to the change of the PMA is used as the molecular detection mechanism in the disclosed invention.
The physical phenomenon of the PMA and the reason, why the orbital deformation defines the strength of the PMA, are explained as follows. Figure 2 shows a cross‐section of a nanomagnet as an array of its electronic orbitals. The magnetization of a thicker film (Fig. 2a) is in-plane, while the magnetization of a thinner film (Fig.2b) is perpendicular-to-plane. The PMA is the reason, why the magnetization changes its direction depending on the film thickness. The equilibrium magnetization direction is the direction of the smallest magnetic energy of the whole film. For the bulk electrons the magnetic energy is smallest when the magnetization is in-plane. For the interface electrons the magnetic energy is smallest when the magnetization is perpendicular-to-plane. In the case of a thicker film, the number of bulk electrons is larger and the total magnetic energy of the film is smaller when the magnetization is in-plane. In the case of a thinner film, the number of bulk electrons is smaller while the number of interface electrons remains the same. As a result, the magnetization becomes perpendicular-to-plane for the substantially thin film.
Origin of PMA |
||
|---|---|---|
| orbital deformation at interface & equilibrium magnetization direction | ||
|
||
Fig.2. The dependence of magnetization of a ferromagnetic film on the orbital deformation of interface atom of a ferromagnetic film. The cross-section of a nanomagnet is shown as an array of its electronic orbitals. The arrow shows the magnetization direction of the nanomagnet. (a) The interface orbitals are spherical and not deformed. The magnetization is in-plane. (b) The interface orbitals are deformed perpendicularly to the plane. The magnetization is perpendicular -to -plane |
The reason why the dependence of the magnetic energy on the magnetization direction is different for the bulk and interface electrons, is their orbital shape. The orbital of the bulk electrons is spherical. They do not experience any HSO. The magnetic energy E||,b and E⊥,b of a bulk electron for the case of in-plane and perpendicular-to-plane magnetization can be calculated as

where S is electron spin, μB is the Bohr magneton, HM is the intrinsic magnetic field induced by the magnetization, HD is the demagnetization field, which is directed perpendicular-to-plane and proportional to the perpendicular component of the HM. DEB is the difference of the magnetic energy for two magnetization directions. For the bulk electron, the DEB is negative.
The interface electrons experience the spin-orbit magnetic field HSO, additionally to HM and HD, because their orbitals are deformed. The HSO is a non-zero only when the magnetization direction is along the deformation and therefore perpendicular-to-plane. For an interface electron, the magnetic energies E||,i and E⊥,i for the in-plane and perpendicular-to-plane magnetizations, respectively, and their difference DEi can be calculated as
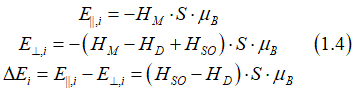
The HSO is proportional to the degree of the orbital deformation. Even when the deformation is small, HSO > HD and the ΔEi is positive. The difference of the magnetic energy for the || and ⊥ magnetization directions is called the PMA energy (EPMA) and can be calculated as
![]()
where NB and Ni are the numbers of the bulk and surface electrons, correspondingly. Since ΔEB is negative, Eq. (1.5) can be simplified as
Origin of PMA |
|---|
| equilibrium magnetization direction vs film thickness |
 |
Fig.3. The total magnetic energy Emag,total of a FeB film as a function of the film thickness. The negative energy means that magnetization is in-plane. Two cases of a different values of the interface energy (Emag,total=1.15 mJ/m2 for solid line and Emag,total=0.85 mJ/m2 for dash line) are shown. In the case of film thickness of 1 nm, the magnetization direction of the film changes from in-plane direction to perpendicular-to-plane direction when Emag,total increases from 0.85 mJ/m2 to 1.15 mJ/m2 |
| click on image to enlarge it |
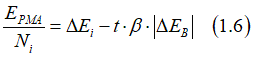
where t is the film thickness, β is the constant, which depends on the symmetry of crystal lattice. In the simplest case of a cubic lattice, it can be calculated as
![]()
where a is the lattice constant.
Figure 3 shows the energy of the perpendicular magnetic anisotropy EPMA of a FeB thin film as function of its thickness for two cases of different orbital deformation at the interface with the interface magnetization ΔEi of 1.15 and 0.85 mJ/m2. The magnetization of the thinner film is perpendicular-to-plane. The magnetization of the thicker film is in-plane. The thickness of the film at which the magnetization changes direction depends on the degree of orbital deformation at the interface and therefore on the value of interface magnetization energy ΔEi. For example, at the thickness of 1 nm, the magnetization can be switched between the in-plane and perpendicular-to-plane directions by the modulation of the orbital deformation.
The orbital deformation at interface can be of two types. The orbital can be elongated or shortened along the interface normal. Both types of the orbital deformation lead to the increase of the HSO and the PMA energy.
The spin-orbit interaction is stronger in the case of a non-symmetrical electron orbital. The less symmetrical orbital is, the stronger HSO the electron experiences.
The spin-orbit interaction is weaker when induced by centrosymmetric electrical field. Even though the p- and d-orbital of a hydrogen atom is non-symmetrical, the HSO is small for the p- and d- electrons in this fully centrosymmetric electrical field of one nucleus. The case is different, when many atoms interacts. Such interaction makes their orbits non-symmetrical. The case of an atom at an interface is prominent. At two side of the interface the atom experience different electrostatic force, which makes the atom orbital well non-symmetric. As a result, the electron of this orbital experience the strong HSO.
Perpendicular-to-plane magnetic anisotropy at a Fe/Pt interface |
||||
|
||||
| Schematic diagram of Pt/Fe interface. The blue and red spheres show the electron orbitals in Fe and Co, respectively. Blue arrows shows the magnetization (spin of localized d-electrons). The green arrows show the effective magnetic field HSO of the spin-orbit interaction. The orbital of the localized electrons are shown. | ||||
| click on image to enlarge it |
It does not matter whether orbital is elongated or squeezed. Both deformations induce the same polarity of the change of HSO. A breaking the spacial symmetry is important, but not the polarity of the breaking. The most effective enhancement of HSO is when the center of electron orbital is shift of the position of the nucleus. (See more details in the spin-orbit interaction)
Yes, very much. The interface PMA exists only at a very smooth interface. Even a moderate roughness of the interface causes the reduction and disappearance of the PMA.
Yes, in the case of the interface-type PMA, the PMA increases when the ferromagnetic layer becomes thinner. See Fig.3
Yes, it is possible. See Fig.3. However, often when the ferromagnetic film or layer becomes very thin, the film roughness sharply increase and even the film may becomes discontinuous. It causes reduction and disappearance of the PMA. However, there sever growth techniques (tricks), which allow to grow a very thin or thick layers with a high PMA.
For example, using a conventional sputtering of amorphous FeB on amorphous SiO2 it is only possible to grow film with perpendicular magnetization in the range of thicknesses between 0.8 nm and 1.5 nm. I have made FeB with strong PMA and perpendicular magnetization as thin as 0.1 nm and as thick as 2.5 nm.
Thickness-dependence of PMA |
||||
|
||||
Fig.16. Magnetization of CoFeB film grown on MgO. The magnetization of a thick film (thickness >1.5 nm) is in-plane , but the magnetization of a thinner film is perpendicular-to-plane |
Yes. It is the case of a single crystal metal with anisotropy axes along the film normal. Another case is the asymmetrical rearrangement of atoms along growth direction. For example, FeTbB has a strong bulk type PMA. Also, it has a weak the the interface PMA. As a result, The equilibrium magnetization of a thin FeTbB is in-plane and a thick FeTbB is perpendicular-to- plane. The slope of Fig.3 becomes positive instead of negative.
There are many possible interfaces with a strong PMA. The famous interfaces are: (1) Co(111)/Pt(111); (2) Fe(001)/ MgO (001); (3) Fe/Ta; (4) Fe/W
The strength of the PMA depends very much on growth technique. It means how thin film and smooth the interface can be obtained.
Relativistic origin of the Spin-Orbit Interaction |
|---|
 |
| An object (red) is moving in a static electric field. In the coordinate system moving together with the object, the static electric field is relativistically transformed into the effective electric field Eeff and the effective magnetic field Heff. The effective magnetic field is called the effective magnetic field of SO interaction HSO . The HSO is absolutely ordinary magnetic field For example, in case if the particle has a magnetic moment (spin), there will be a spin precession around the HSO. |
| click on image to enlarge it |
| more details is here |
for more details see here
Fact 1. ![]() Relativistic origin of spin-orbit interaction
Relativistic origin of spin-orbit interaction
An object, which moves in an electrical field, experience an effective magnetic field. This effective magnetic field is 100% magnetic field and it is indistinguishable from any other magnetic field.
This magnetic field is called the SO magnetic field HSO.
The origin of the SO magnetic field is the relativistic nature of the electromagnetic field.
Fact 2. ![]() The electrical field of atomic nucleus induces the SO magnetic field, which originates the perpendicular magnetic anisotropy (PMA)
The electrical field of atomic nucleus induces the SO magnetic field, which originates the perpendicular magnetic anisotropy (PMA)
Because of its relativistic nature, the SO effect is weak. Only a very strong electrical field may induce sizable SO magnetic field. Only the electrical field of atomic nucleus is sufficient strong to create sufficiently strong SO magnetic field (1-30 kGauss), which induces the PMA
Fact 3. ![]() Only an electron in a non-symmetrical orbital experiences SO interaction
Only an electron in a non-symmetrical orbital experiences SO interaction
Key properties of SO interaction: Enhancement of magnetic field due to SO interaction |
The external magnetic field Hext induces the effective magnetic field of the spin-orbit interaction HSO, which is is in the same direction as the external magnetic field.. Therefore, the total magnetic field, which the electron experiences, becomes larger. The deformed electron orbital is shown. click here or on image to enlarge it |
| More details are here |
An electron in spherical orbital (s -orbital) does not experience any SO interaction (explanation is here). Only when orbital symmetry is broken, the electron experience SO interactions.
There are several possibilities to break the orbital symmetry. Each of them induces HSO. The magnitude HSO is proportional to the degree of the breaking symmetry.
Fact 4. ![]() The electrical field of nucleus cannot break time- inverse symmetry. The SO magnetic field exists only when there is external magnetic field.
The electrical field of nucleus cannot break time- inverse symmetry. The SO magnetic field exists only when there is external magnetic field.
The HSO exists only when there is some external magnetic field.
The HSO is always is zero in absence of the external magnetic field.
The HSO is always in the same direction as the external magnetic field.
The HSO may be significantly larger than the external magnetic field
Fact 5. ![]() The SO is direction dependent. It is the source of the PMA
The SO is direction dependent. It is the source of the PMA
When orbital is deformed only in one direction (for example, only along the z- direction), the HSO exists only when the external magnetic field is directed along this direction (along the z-direction), but there is no HSO when the external magnetic field is directed in a different direction (along the x- or y- direction)
When the orbital is deformed perpendicularly to the film interface, the HSO is induced only in this direction. The directional dependence of HSO originates the PMA (See below)
Fact 6. ![]() The orbital symmetry in close proximity to nucleus determine the strength of the SO magnetic field
The orbital symmetry in close proximity to nucleus determine the strength of the SO magnetic field
The increase of the spin-orbit interaction due to deformation of the electron orbital |
||||
|
||||
| Electron orbital. When the orbital is spherical and its center at the position of the nucleus, the effective magnetic field of the spin-orbit interaction HSO is zero. Only when the orbital is deformed, there is the magnetic field of the spin-orbit interaction. |
A substantial SO is induced only by a very strong magnetic field, which exists only in very close proximity to nucleus. Only this region makes substantial contribution to the HSO and EPMA. For this reason, the orbital symmetry in this region is critically important for the PMA.
As a result: HSO is larger when the center of orbital slightly shifted from the position of the nucleus comparing to a slight deformation of
Fact 7. ![]() Mainly localized d- or f- electrons contribute to PMA
Mainly localized d- or f- electrons contribute to PMA
Spins of the localized d- or f- electrons mainly contribute to the magnetization of a ferromagnetic metal. Therefore, the deformation and symmetry of these orbitals mainly determines the PMA.
The contribution of the conduction electrons to the metal magnetization and the PMA exists, but it is very small. It is because the distribution of the spin directions of the conduction electrons is very different from that of localized d- or f- electrons (See here)
The conduction electrons influence the PMA and the magnetization mainly due to the sp-d exchange interaction.
Q. The orbital of d- and f- electrons are already not spherical. Do they experience the SO interaction and the magnetic anisotropy?
A. It is correct. They do. There is magnetic anisotropy along some crystal orientation. Often it is not large. However, at the interface the orbital deformation might be much larger, which induces much larger HSO and EPMA.
See also VCMA effect and SO torque
Fact 8. ![]() The parity symmetry and spin-orbit interaction
The parity symmetry and spin-orbit interaction
Parity symmetry of SO interaction |
The HSO does not dependent on wether the electron orbital is shifted along Hext or in opposite direction. This feature is called the parity symmetry of SO interaction. |
| click on image to enlarge |
The SO interaction and the PMA depend only the direction of orbital deformation, but not its polarity.
For example, the orbital deformation due to a shift of the center of electron orbit from position of atomic nucleus in + x direction induces absolutely equal HSO and EPMA
as the shift in - x direction.
Fact 8. ![]() Neither covalent nor ionic bonding is good for PMA and SO. The optimum bonding should be something between.
Neither covalent nor ionic bonding is good for PMA and SO. The optimum bonding should be something between.
In both case of the covalent bonding (E.g. Si, Fe) or the ionic bonding (E.g. NaCl, ZnO), the electron orbital is rather symmetric to induce any HSO and EPMA. In order to induce a large magnetic anisotropy, the orbital should be deformed asymmetrically. It is the case when the bonding is neither fully covalent nor fully ionic.
A bonding across an interface (the interfacial PMA) or a bonding along some specific crystal direction in a compound crystal (E.g. CoPt, SmCo, GaAs, InP) (bulk-type PMA) make optimum orbital deformation and induce a strong HSO and EPMA
Physical Origin of perpendicular magnetic anisotropy (PMA)
Origin of PMA: Directional dependence of HSO |
The electron orbital is deformed only in z-direction (for example,toward film interface). The external magnetic field Hext induces the effective magnetic field of the spin-orbit interaction HSO, which is is in the same direction as the external magnetic field. When Hext is directed along z-axis, HSO is large, because the orbital is deformed in this direction. When Hext is directed along y- or x-axis, HSO is zero because the orbital is symmetrical in this direction. . |
| click on image to enlarge it |
The PMA exists, because the electron orbitals in a ferromagnetic metal are deformed in the direction perpendicular to the film interface. When magnetization is along this direction, the intrinsic magnetic field induced a substantial effective magnetic field of the spin-orbit interaction HSO , because orbital deformation in this direction. When the magnetization is in-plane, there is no HSO, because the orbital is not deformed in this direction. As a result, the absolute value of the magnetic energy increases, when the magnetization is perpendicular to the film, and decreases when the magnetization is in plane.
Magnetization is in plane:
Total magnetic field= Hintristic
Magnetic energy= -Hintristic · M
Magnetization is perpendicular to plane:
Total magnetic field= Hintristic+HSO
Magnetic energy= -(Hintristic +HSO )· M
where M is the magnetization or the spin of localized electrons.
Since the absolute value of the negative magnetic energy is larger in the case when the magnetization is perpendicular-to-plane. As a result, the easy magnetization direction becomes perpendicular-to-plane, because of the SO interaction
note: See also about demagnetization field
Measurement of anisotropy field Hanis |
||
|
||
| Measured in-plane magnetization as a function of applied in-plane magnetic field. The arrow shows the direction and magnitude of the applied in-plane magnetic field. The ball shows the magnetization direction. Without magnetic field the magnetization is perpendicularly-to-plane. Under magnetic field, the magnetization turns toward magnetic field. The field, at which the magnetization turns completely in-plane, is called the anisotropy field. The dots of the right graph shows experimental data. Measurement date: May 2018. | ||
| Click on image to enlarge it |
![]() Important feature of PMA: Linear dependence of in-plane component of magnetization on in plane magnetic field. See below the math to prove it. Since the fitting of a linear dependence is simpler, is resisted against the noise and other unwanted disturbing factors (like magnetic domain) and can be done with a high precision, measuring of Hanisotropy with a high precision is an important step to almost any magneto transport measurement.
Important feature of PMA: Linear dependence of in-plane component of magnetization on in plane magnetic field. See below the math to prove it. Since the fitting of a linear dependence is simpler, is resisted against the noise and other unwanted disturbing factors (like magnetic domain) and can be done with a high precision, measuring of Hanisotropy with a high precision is an important step to almost any magneto transport measurement.
Important facts about the spin-orbit interaction and PMA are:
![]() fact 1: Due to the spin-orbit interaction, there is a strong magnetic along the film normal (the z-axis). This magnetic field is called the magnetic field of the SO interaction. It is absolutely real magnetic field, which is generated relativistically due to electron movement in electrical field of atomic nucleus
fact 1: Due to the spin-orbit interaction, there is a strong magnetic along the film normal (the z-axis). This magnetic field is called the magnetic field of the SO interaction. It is absolutely real magnetic field, which is generated relativistically due to electron movement in electrical field of atomic nucleus
![]() fact 2: The SO magnetic field is generated due to the orbital deformation along the z-axis. In the case of the uniaxial anisotropy it can be simplified that there is a SO magnetic field only along z-axis, but there is no in-plane SO magnetic field. There is no field along the x-axis and y-axis. The magnitude of the SO magnetic field is proportional to degree of deformation of electron orbital in close proximity to atomic nucleus.
fact 2: The SO magnetic field is generated due to the orbital deformation along the z-axis. In the case of the uniaxial anisotropy it can be simplified that there is a SO magnetic field only along z-axis, but there is no in-plane SO magnetic field. There is no field along the x-axis and y-axis. The magnitude of the SO magnetic field is proportional to degree of deformation of electron orbital in close proximity to atomic nucleus.
![]() fact 3: The magnitude of the SO magnetic field is linearly proportional to the total magnetic field along the z- direction (perpendicularly to interface).
fact 3: The magnitude of the SO magnetic field is linearly proportional to the total magnetic field along the z- direction (perpendicularly to interface).
(note) ![]() The calculation is for a single electron. In the case, when orbital symmetry of the electrons in bulk and at an interface is different, the effective anisotropy field for the whole nanomagnet should be calculated (See here)
The calculation is for a single electron. In the case, when orbital symmetry of the electrons in bulk and at an interface is different, the effective anisotropy field for the whole nanomagnet should be calculated (See here)
(how calculation is done)![]() The angle of magnetization turning is calculated by a minimizing the magnetic energy for electron spin. The magnetic energy is the product of the electron spin and a sum of all magnetic fields, which the electron experiences.
The angle of magnetization turning is calculated by a minimizing the magnetic energy for electron spin. The magnetic energy is the product of the electron spin and a sum of all magnetic fields, which the electron experiences.
![]()
![]()
![]()
![]() Magnetic fields, which the electron experiences:
Magnetic fields, which the electron experiences:
(field 1): ![]()
![]() External magnetic field, which is applied in both the perpendicular- to- interface direction Hz and in the in-plane direction Hx.
External magnetic field, which is applied in both the perpendicular- to- interface direction Hz and in the in-plane direction Hx.
(field 2): ![]()
![]() Magnetic field of magnetization induced by all aligned electrons in a nanomagnet. This field can be imagined as a magnetic field inside the magnetic dipole induced by the electron spin. The average spin is a nanomagnet called the magnetization M. The magnetic field of magnetization is linearly proportional to the electron spin. In simplified units, the magnetic field induced by the spin equals to M.
Magnetic field of magnetization induced by all aligned electrons in a nanomagnet. This field can be imagined as a magnetic field inside the magnetic dipole induced by the electron spin. The average spin is a nanomagnet called the magnetization M. The magnetic field of magnetization is linearly proportional to the electron spin. In simplified units, the magnetic field induced by the spin equals to M.
(field 3)![]()
![]() Demagnetization field Hdemag. The magnetic field, which is generated at interface due to broken chain of aligned spins. The direction of Hdemag is perpendicular- to- interface and opposite to M. The Hdemag can be calculated as
Demagnetization field Hdemag. The magnetic field, which is generated at interface due to broken chain of aligned spins. The direction of Hdemag is perpendicular- to- interface and opposite to M. The Hdemag can be calculated as
![]()
where kdemag is the demagnetization factor.
(field 4)![]()
![]() Magnetic field HSO of spin- orbit interaction, which is a relativistic magnetic field induced by an electrical field of atomic nucleus. It is directed along the orbital deformation (the z- direction in this case) and is proportional to the total magnetic field, which is applied along the x- direction.
Magnetic field HSO of spin- orbit interaction, which is a relativistic magnetic field induced by an electrical field of atomic nucleus. It is directed along the orbital deformation (the z- direction in this case) and is proportional to the total magnetic field, which is applied along the x- direction.
![]()
where kSO is a parameter describing the strength of the spin- orbit interaction, is the intrinsic field in the nanomagnet and M is the magnetization of the nanomagnet
(intrinsic field=field2+field3) ![]() It is magnetic field, which all atom in nanomagnet equally experience. In contrast, the spin-orbit field HSO (field 4) is individual for each atom (not common), because HSO is linearly proportional to the orbital deformation (See here), which is very different for each atom. ( example: a Fe nanomagnet) At an interface orbital deformation of Fe atoms is large and interfacial Fe atoms experience a large HSO. However a few atomic layers below, the orbital of Fe is not deformed and these experience no HSO.
It is magnetic field, which all atom in nanomagnet equally experience. In contrast, the spin-orbit field HSO (field 4) is individual for each atom (not common), because HSO is linearly proportional to the orbital deformation (See here), which is very different for each atom. ( example: a Fe nanomagnet) At an interface orbital deformation of Fe atoms is large and interfacial Fe atoms experience a large HSO. However a few atomic layers below, the orbital of Fe is not deformed and these experience no HSO.
Measurement of anisotropy field |
 |
Measurement of the anisotropy field of a magnetic nanowire. Without an external magnetic, the magnetization M is perpendicular to the film due to PMA. When external in-plane magnetic field Hext is applied, the magnetization turns. The magnetic field , at which the magnetization turns fully in-plane is called the anisotropy field |
| Click on image to enlarge it |
The magnetization direction under an external in-plane magnetic field is calculated from minimizing the magnetic energy. In the case of zero orbital moment, the magnetic energy of an electron is a product of electron spin M and a sum of all magnetic fields, which the electron experiences: Hall=H+M+ Hdemag + HSO. The magnetic energy can be calculated as
![]()
---------------
Case 1: There is no perpendicular external magnetic field Hz =0
In this case (Hz=0), the magnetic energy Eq.(2.4) is calculated as
![]()
Under an in-plane magnetic field Hx, the magnetization M does not change its magnitude only its direction turns. As a result, M is a constant and independent of Hx. Eq.(2.5) can be written as
![]()
The equilibrium magnetization direction corresponds to the minimum magnetic energy. Minimizing the energy with respect to Mx gives
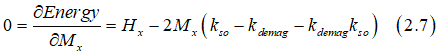
The solution of Eq.(2.7) gives the linear dependence of in-plane component Mx of the magnetization on the in-plane magnetic field Hx as

where the anisotropy field Hanis is calculated as
![]()
| Anisotropy field. Calculations vs. Measurement | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
| Calculation predicts an nearly- linear increase of the anisotropy field when the external field H increases. The experimental measurements confirms the linear increase with H at at a larger field, but dependence deviate from linear at a smaller field | |||||||||
| Click on image to enlarge it |
---------------
Case 2: There is a perpendicular external magnetic field Hz≠ 0
In this case the magnetic energy can be calculated as (See Eq.2.4)

where H(0)anis is the anisotropy field in the absence of the external magnetic field (Hz =0)
The equilibrium magnetization direction corresponds to the minimum magnetic energy. Minimizing the energy with respect to Mx gives

The solution of Eq.(2.7) is
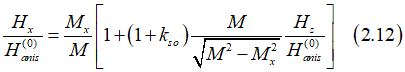
Even though the dependence of Eq.(2.12) deviates from linear, it is close to a linear dependence and can be expressed similar to Eq.(9) as

| Fig.30 Anisotropy field. Calculations vs. Measurement | ||||||
|---|---|---|---|---|---|---|
|
||||||
| Parameters used in calculations Hanis,0=4 kG; kSO =0.2. Hz=2 kG; | ||||||
| Click on image to enlarge it |
in which the anisotropy field depends on Hz and can be calculated as
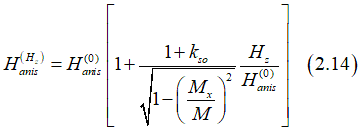
Substitution Eq.(2.13) into Eq. (2.14) gives the effective anisotropy field as
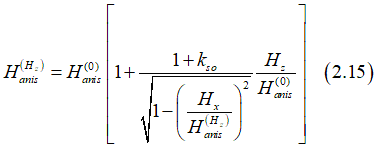
From Eq.(2.15), the anisotropy field depends linearly on the external perpendicular magnetic field Hz.
When the applied in-plane magnetic field is much smaller than the anisotropy field
![]()
Eq.(2.15) is simplified to

and therefore the effective anisotropy field becomes independent of Hx
When condition (2.16) is not the case, Eq. (2.15) can be solved by an iteration starting from Eq.(2.17)
Figure 30 shows that the independence of the anisotropy field on in-plane magnetic field and the linear dependence of Mx vs. Hx is a good approximation for the most of a realistic nanomagnets.
Experiment. Measurement of anisotropy field |
||||
|
||||
Measurement of the anisotropy field of a magnetic nanowire. The green balls shows the magnetization direction of FeB nanomagnet, the blue arrow shows direction of external magnetic field. The FeB nanomagnet is fabricated on top of Ta nanowire. The magnetization direction is measured by a pair of Hall probe. The measured Hall voltage is largest when the magnetization is perpendicular to the top surface of nanomagnet |
||||
| Without an external magnetic, the magnetization M is perpendicular to the film due to PMA. When external in-plane magnetic field H|| is applied, the magnetization turns towards the H||. The magnetic field, at which the magnetization turns fully in-plane is called the anisotropy field. The stronger PMA is and the stronger the PMA resists to the magnetization turning, the lager and the anisotropy filed is. Therefore, the anisotropy field is measure of the strength of the PMA. | ||||
| Click on image to enlarge it |
 PMA energy
PMA energy(method 1 of calculation of PMA energy) imaginable switching off the spin- orbit interaction and demagnetization effect
imaginable switching off the spin- orbit interaction and demagnetization effect
In case when there is no external magnetic field (Hx=0; Hz=0) , the magnetization is perpendicular to plane (Mx=0; Mz=M) and the magnetic energy can be calculated from Eqs. (2.6,2.9) as
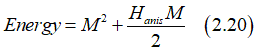
If we switch off the spin- orbit interaction kSO=0 and demagnetization field kdemag=0 (just imagine it), kSO=0 becomes zero and the magnetic energy is calculated as
![]()
The PMA energy EPMA is defined as an energy, which is induced by the spin-orbit interaction minus demagnetization. Comparison of Eqs.(12) and 813) gives the PMA energy as
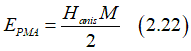
(note 1) The anisotropy field Hanis is the parameter, which characterizes the PMA energy.
The anisotropy field Hanis is the parameter, which characterizes the PMA energy.
(note 2) In the case, when orbital symmetry of the electrons in bulk and at an interface is different, the effective PMA energy for the whole nanomagnet should be calculated (See above).
In the case, when orbital symmetry of the electrons in bulk and at an interface is different, the effective PMA energy for the whole nanomagnet should be calculated (See above).
(note 1) The PMA energy can be either positive (equilibrium magnetization is perpendicular to plane) or negative (equilibrium magnetization is in- plane). From Eq.(10) the condition when the PMA energy is positive is
The PMA energy can be either positive (equilibrium magnetization is perpendicular to plane) or negative (equilibrium magnetization is in- plane). From Eq.(10) the condition when the PMA energy is positive is
![]()
(method 2 of calculation of PMA energy) integration over a path of turning magnetization from a perpendicular-to-plane to in-plane direction
integration over a path of turning magnetization from a perpendicular-to-plane to in-plane direction
The PMA energy can be also defined as an energy, which is required in order to turn the magnetization fully in-plane. A tiny change dHx of in-plane magnetic field correspond to a change of magnetic energy dHx · Mx. The integration over the change of Hx from 0 to Hanis using Eq.(2.8) gives the PMA energy as
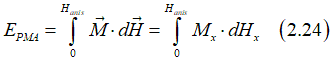
Effective Internal magnetic field in a nanomagnet |
||||||||||||
| It has both in-plane and perpendicular- to- plane components.; nanomagnet easy axis is perpendicular-to-plane; external magnetic field is applied in the in-plane direction | ||||||||||||
|
||||||||||||
| In absence of external field HII=0, the internal magnetic field Hint equals to Hint=M+Hani and is directed perpendicularly- to film normal. Under a large in-plane magnetic field HII> Hani, both the magnetization and the internal magnetic field are in-plane and Hint=M. | ||||||||||||
| The data was calculated from Eq.(5.20). See here. | ||||||||||||
| Click on image to enlarge it |
There is a magnetic field inside nanomagnet, which is called the internal magnetic field .
(note about magnetic field of spin-orbit interaction ![]() ): The localized electrons on the surface and in the bulk of the nanomagnet experience a different magnetic field due to the spin-orbit interaction. The magnetic field HSO of spin- orbit interaction is individual for each electron and depends on its orbital symmetry (See here). The electron at interface experience a strong HSO. In the contrast, the electrons in the bulk of the nanomagnet experience a weak HSO. As a result, the same electrons experience a very magnetic field at interface and in the bulk.
): The localized electrons on the surface and in the bulk of the nanomagnet experience a different magnetic field due to the spin-orbit interaction. The magnetic field HSO of spin- orbit interaction is individual for each electron and depends on its orbital symmetry (See here). The electron at interface experience a strong HSO. In the contrast, the electrons in the bulk of the nanomagnet experience a weak HSO. As a result, the same electrons experience a very magnetic field at interface and in the bulk.
(note fixing spins of all electrons in one direction ![]() ): localized electron in a ferromagnetic material experience a substantial exchange interaction (See here).The effective magnetic field of the exchange interaction is very large (~1500 T See here). Since it is so large, the exchange field solidifies all spins in one direction. As a result, the whole nanomagnet can be consider as a single spin object with united total spin.
): localized electron in a ferromagnetic material experience a substantial exchange interaction (See here).The effective magnetic field of the exchange interaction is very large (~1500 T See here). Since it is so large, the exchange field solidifies all spins in one direction. As a result, the whole nanomagnet can be consider as a single spin object with united total spin.
(type 1) ![]() Effective internal magnetic field
Effective internal magnetic field
Even though the electrons at interface and bulk experience a different internal magnetic field, the total spin of nanomagnet experience an average of all those contributions. This magnetic field affects the total spin of the nanomagnet. This is the internal magnetic field, which by the nanomagnet as one object. For example, this internal magnetic field determines properties of the ferromagnetic resonance (FMR) of the nanomagnet.
(type 2) ![]() Global internal magnetic field
Global internal magnetic field
This is the conventional magnetic filed, which is inside of the nanomagnet (See here). This magnetic field "fills" all the space inside the nanomagnet and all other spin objects (e.g. spin of a nucleus) equally experience this magnetic field.
Internal magnetic field in a nanomagnet. Measurements. |
||||||||
| Measurements: Sample Volt40A nanomagnet L43C (all measurement data see here) | ||||||||
|
||||||||
| Click on image to enlarge it |
(fact 1 about field when magnetization is in-plane) ![]() When magnetization is in-plane, both the effective internal magnetic field and the global magnetic field equals to M (magnetic field induced by the magnetization) E.g. in the case of FeB nanomagnet (See here) this field is about 14 kGauss. This fact is applied for both types of the nanomagnets with in-plane and perpendicular-to-plane equilibrium magnetization.
When magnetization is in-plane, both the effective internal magnetic field and the global magnetic field equals to M (magnetic field induced by the magnetization) E.g. in the case of FeB nanomagnet (See here) this field is about 14 kGauss. This fact is applied for both types of the nanomagnets with in-plane and perpendicular-to-plane equilibrium magnetization.
(fact 2 about global internal field when magnetization is perpendicular- to-plane ) ![]() When magnetization is perpendicular-to-plane the global internal magnetic field is zero. This fact is applied for both types of the nanomagnets with in-plane and perpendicular-to-plane equilibrium magnetization.
When magnetization is perpendicular-to-plane the global internal magnetic field is zero. This fact is applied for both types of the nanomagnets with in-plane and perpendicular-to-plane equilibrium magnetization.
(fact 3 about effective internal field when magnetization is perpendicular- to-plane ) ![]() (case when the equilibrium magnetization the nanomagnet is perpendicular-to-plane ):
(case when the equilibrium magnetization the nanomagnet is perpendicular-to-plane ):![]()
![]() When magnetization is perpendicular-to-plane, the effective internal magnetic field equals to M+Hani (the sum of magnetic field induced by the magnetization and the anisotropy field). E.g. in the case of FeB nanomagnet (See here), M ~14 kGauss and HSO ~6 kGauss, therefore the effective internal magnetic field is about 20 kGauss=2 T.
When magnetization is perpendicular-to-plane, the effective internal magnetic field equals to M+Hani (the sum of magnetic field induced by the magnetization and the anisotropy field). E.g. in the case of FeB nanomagnet (See here), M ~14 kGauss and HSO ~6 kGauss, therefore the effective internal magnetic field is about 20 kGauss=2 T.
(fact 4 about effective internal field when magnetization is perpendicular- to-plane ) ![]() (case when the equilibrium magnetization the nanomagnet is in-plane ):
(case when the equilibrium magnetization the nanomagnet is in-plane ): ![]() When a sufficient external magnetic field is applied so that the nanomagnet magnetization turns to perpendicular-to-plane direction, the effective internal magnetic field is between zero (case of no PMA) to M (case of some PMA). E.g. in the case of FeB nanomagnet, M ~14 kGauss, therefore the effective internal magnetic field is between 0 kGauss (e.g. a thick FeB film) and 14 kGauss. (e.g. a thin FeB film)
When a sufficient external magnetic field is applied so that the nanomagnet magnetization turns to perpendicular-to-plane direction, the effective internal magnetic field is between zero (case of no PMA) to M (case of some PMA). E.g. in the case of FeB nanomagnet, M ~14 kGauss, therefore the effective internal magnetic field is between 0 kGauss (e.g. a thick FeB film) and 14 kGauss. (e.g. a thin FeB film)
(fact 5 about an increase of effective internal field under applied external magnetic field) ![]() when the magnetization is perpendicular- to- plane and an external magnetic film is applied in the same direction, the effective internal field increases with increase proportionally to the increase of the external magnetic field due to the increase of the magnetic field of the spin- orbit interaction (See here). The external perpendicular magnetic field does not affect the global internal field.
when the magnetization is perpendicular- to- plane and an external magnetic film is applied in the same direction, the effective internal field increases with increase proportionally to the increase of the external magnetic field due to the increase of the magnetic field of the spin- orbit interaction (See here). The external perpendicular magnetic field does not affect the global internal field.

Effective internal magnetic field: ![]()
![]()
![]()
perpendicular- to- plane component: ![]()
![]()
![]()
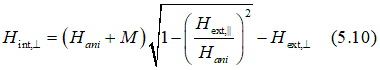
in-plane component:![]()
![]()
![]()
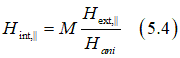
Global internal magnetic field: ![]()
![]()
![]()
perpendicular to plane component: ![]()
![]()
in-plane component:![]()
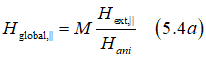
where M is magnetization (~14 kGauss for FeB); Hani is the anisotropy field (~2-10 kGauss for FeB); and Hext are in-plane and perpendicular-to-plane of applied external magnetic field.
3 following experimental method are most often used to measure Hanisotropy
The magnetometer measures the magnetization. From measurement of the in-plane magnetization as a function of in-plane magnetic field, the linear fitting by Eq.(2.10) gives Hanisotropy.
merit: High-reliability direct measurements
weak-points: Due to sensitivity limitations, only a relatively large samples can be measured.
The Hall angle is linearly proportional to perpendicular component of the magnetization (See here). The measurement of the Hall angle as a function of in-plane magnetic field gives dependence Mx/M. The linear fitting by Eq.(2.10) gives Hanisotropy.
merits: (1) Nano-sized object can be measured (2) It can be combined with other magneto-transport measurements
weak-points: (1) Its measurement precision is rather sensitive to existence of magnetic domains. (2) It takes a relative a long time for a measurement.
The method uses a magnetic tunnel junction (MTJ), in which the magnetization of the “reference” layer is in-plane and the magnetization of the “free” layer is perpendicular-to-plane. When a magnetic field is applied in the in-plane direction, the magnetization of the “free” layer turns toward the magnetic field. From the measurement of the tunnel resistance, the angle between “free” and “reference” layers is calculated. It gives in-plane component of magnetization of "free" layer vs the in-plane magnetic field. From this data, the linear fitting by Eq.(2.10) gives Hanisotropy.
merits: (1) Nano-sized object can be measured (2) It can be combined with other magneto-transport measurements (3) It is fast measurements
weak-points: (1) Comparing with previous two methods, it is more indirect measurement. It is easy to get a systematical error with this method. (2) there is an undesirable influence of the dipole magnetic field from the reference electrode (3) The MTJ configuration is limited to a specific ferromagnetic metal, which has to provide a sufficient magneto resistance.
Switching time influenced by different effects |
||||||||||||
|
||||||||||||
| Click on image to enlarge it. |
Doing the Science has never been easy |
 |
In contrast, the production of fakes in a larger numbers is much easier |
| Click on image to enlarge it |
Under a strong magnetic field, the dependence the spin-orbit interaction and consequently PMA from perpendicular magnetic field deviates from a linear dependence. There are several reasons for that. The first reason is that the magnetic field may deform the atomic orbital, which enhances the SO and consequently PMA. As a result, the strength GSO of the spin-orbit interaction (See Eq. 2.1) becomes dependent on the magnetic field. As was explained here, the breaking the symmetry only along the z-direction (perpendicularly to the interface) affects the PMA, the GSO may be changed only by Hz .Than, Eq. 2.1 can be re- written as

where HSO is the effective magnetic field of SO interactions; GSO is the proportionality constant; Hintristic,z is the z-component of the total magnetic field; Hnl is the magnetic field, at which the strength of SO interaction increases in two times. It means the proportionality coefficient between HSO and Hintristic,z increases in two times. Hnl is usually substantially larger than magnetization M. Usually it is about a few Teslas.
![]() Which parameters are influenced by the non-linear SO interaction?
Which parameters are influenced by the non-linear SO interaction?
![]() The dependence of the in-plane component of magnetization vs in-plane magnetic field deviates from linear at the magnetic field close to anisotropy field Hanis (the "non-linear tail")
The dependence of the in-plane component of magnetization vs in-plane magnetic field deviates from linear at the magnetic field close to anisotropy field Hanis (the "non-linear tail")
![]() It changes the value of anisotropy field Hanis
It changes the value of anisotropy field Hanis
the equilibrium magnetization direction can be calculated from
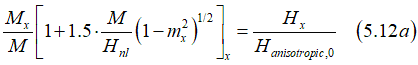
The effective anisotropy field Hanis can be calculated as
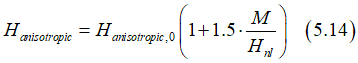
where ![]()
is the anisotropy field in case without any non-linear SO component
Non-linear spin-orbit interaction
The total intrinsic magnetic field is the sum of the extrinsic magnetic field H and the magnetization field M. Therefore, Eq. (5.1) becomes
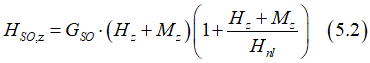
The magnetic energy can be calculated as
![]()
where component proportional to Mz is
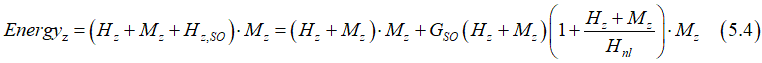
and component proportional to Mx is
![]()
The total energy is the sum of Eqs. (5.3) and (5.4):
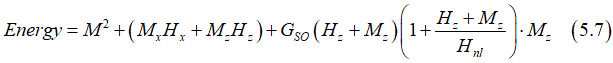
In the case when the magnetic field is applied in-plane (Hx =0), Eq.(5.7) is simplified to
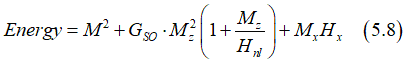
or

where 
The minimum of the energy corresponds to the equilibrium magnetization direction, which can be found as
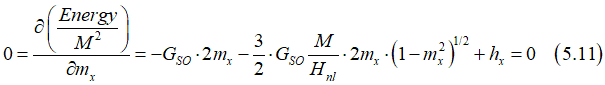
Therefore, the equilibrium magnetization direction can be calculated from
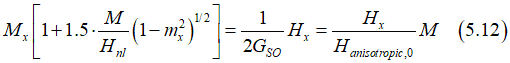
or
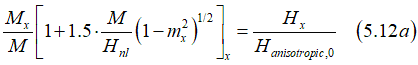
where ![]()
is the anisotropy field in case without any non-linear SO component.
In the case field H is smaller and is not close to Hanis, the following condition is satisfied
![]()
From (5.13), (5.12a) and (2.10) the effective anisotropy field can be calculated as
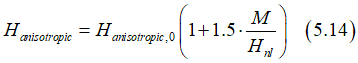
 My pubication on Magnetic anisotropy
My pubication on Magnetic anisotropy
 Measurement of coefficient of spin- orbit interaction and anisotropy field in a nanomagnet.
Measurement of coefficient of spin- orbit interaction and anisotropy field in a nanomagnet.This video set explains the details of a high precision measurement method of the anisotropy field Hani, coefficient of spin-orbit interaction kSO , internal magnetic field in a nanomagnet Hint and a magnetic field Hoff created by a spin-accumulation in a nanomagnet.
I will show you how to do measurement, how to process measured data and how to evaluate each parameter. You can use either my raw measurement data, which you can download, or your own data.
I will describe how to use the measurement data to improve the efficiency of the magnetization reversal either by a electrical current or by a gate voltage for a memory application and for a sensor application
I will explain the details of the magnetization reversal mechanism using the classical mechanics based on LL Eq. and using Quantum mechanics. I will explain the quantum mechanical meaning of the spin torque and the spin precession. I will explain the reasons why the newly-introduced field-like torque severely violates Laws of Quantum mechanics. I will explain about the interpretation problems and possible systematic errors of the popular measurement techniques, which are called the 2nd harmonic measurement and the zero-harmonic measurement. I will give some technological recommendations on how to improve the fabrication of a nanomagnet, which are based on my personal experience.
(video): |
|||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
| click on image to watch YouTube video |
![]() Content of this page represents my personal view and it is reflected my own finding. It may slightly different from the "classical" view on PMA, which is described in following references
Content of this page represents my personal view and it is reflected my own finding. It may slightly different from the "classical" view on PMA, which is described in following references
(about dependency of the spin-orbit interaction of external magnetic field)![]()
![]()
![]()
![]()
Your question is why the spin-orbit interaction depends on an external magnetic field and in which reference it was described for the first time.
This fact is known for a very long time and therefore it is more about the history of Science, in which I am not expert. I am sorry if I refer something incorrectly.
--------------------------------
(SO fact 1) The fact about the relativistic origin of the magnetic field and the existence of the spin-orbit interaction (the existence of the magnetic field of the spin-orbit interaction). This fact is one of basic facts, on which the Special Theory of Relativity was build. Therefore, I think Einstein and Lorentz knew about this fact. Myself, I have read all about this fact (all details and many nice explanations) in Landau textbook "The Classical Theory of Fields"
(SO fact 2) The fact that the strength of spin- orbit interaction (the SO magnetic field) is proportional to the strength of an externally applied magnetic field. This fact are direct consequence of the another important fact about SO:
(SO fact 3) The spin-orbit interaction cannot break the time- inverse symmetry. As a result, in order to manifest itself, the SO needs an external breaking of the time- inverse symmetry (E.g. by an orbital moment or by an external magnetic field or an electrical current etc.).
Fact 2 follows very directly from the fact 3. The strength of SO is zero , when the time inverse- symmetry is not broken (case when the orbital moment is zero, there is no external magnetic field etc.) . The SO magnetic field becomes a non-zero only when the time- inverse symmetry is broken. The strength of the SO ( the strength of the SO magnetic field) becomes larger when the degree of the breaking of the time inverse symmetry becomes larger (e.g. the orbital moment becomes larger or the external magnetic field becomes larger etc.) .
Once again
zero magnetic field -> time-inverse symmetry is not broken -> spin-orbit is zero
external magnetic field becomes larger -> degree of breaking of time-inverse symmetry becomes larger -> spin-orbit becomes larger.
--------------------------------
(fact 3 explanation) Why the spin-orbit interaction cannot break the time- inverse symmetry. This feature is the feature of the time-space symmetry and can be obtained from he Special Theory of Relativity (e.g. see Landau textbook " The Classical Theory of Fields " ). A simplified understanding of the fact 3 can be as follows. The spin-orbit effect is a relativistic effect and therefore can only occur when the object moves or the field, with which the object interacts, moves. The relativistic effect requires a movement. The close movement speed is to the speed of the light, the stronger any relativistic effect is. Any movement means a breaking of the time inverse symmetry. This is why the SO occurs only when the time-inverse symmetry is broken.
------------------------------------
Even though the direct relation between the spin- orbit interaction and the breaking of the time- inverse was understood a long time ago as well as the proportionality of the SO strength to the degree of TIS breaking (e.g., to the strength of the orbital moment or to strength of the external magnetic field), all details and specifics have not been fully understood.
For example, the SO strength depends on the orbital symmetry. Usually the orbital is more symmetric in the bulk of a material and the SO is weaker, but at an interface the orbital becomes less symmetrical and the SO becomes larger.
You can read some details here
This effect is used for molecular-recognition sensor, See here
----------------------------------------------------------------
About experimental measurements.
The dependence of PMA and therefore SO on an external magnetic field is very strong. The experimental measurement of this dependence is rather simple and the measured data well fit to the theory. The anisotropy field is a measurable parameter, which characterizes the strength of PMA and SO.
Near for all nanomagnet, I have studied, I measure the dependence of anisotropy field on a perpendicular magnetic field. Such data contains a lot of important information.
Introductory presentation on this measurement method I gave at MMM 2020 conference. You can watch it here
The spin-orbit interaction is fully responsible for the existence of magnetic anisotropy. Therefore, incorporating the spin-orbit interaction into the Hamiltonian should comprehensively explain all features of magnetic anisotropy. While the oversimplified semi-empirical classical Hamiltonian of magnetic anisotropy explains many features, a full description of all properties of the magnetic anisotropy can be only achieved by correctly including the spin-orbit interaction in the Hamiltonian.
The semi-empirical classical Hamiltonian only describes that magnetic energy is minimized when the magnetization is along the easy magnetic axis and maximized when it is along the hard axis. In contrast, the spin-orbit interaction-based Hamiltonian incorporates conservation laws of space-time, specifically the conservation of T-symmetry. Thus, this Hamiltonian is more general and has a broader validity range. It should be noted that both Hamiltonians often yield similar results. For example, they both predict the important linear relationship between Mx and Hx (Eq. 3 of AIP2024).
A. (2024.03) The perpendicular magnetic anisotropy (PMA) in amorphous FeB nanomagnets arises from the combined effects of spin-orbit interaction (SOI) and the demagnetization field, both of which exhibit a strong dependence on the magnetization direction. This fundamental characteristic is the defining magnetic anisotropy in these nanomagnets.
The demagnetization field reaches its maximum when the magnetization is perpendicular to the plane and vanishes when it is in-plane, favoring an in-plane magnetization configuration. In contrast, interfacial spin-orbit interaction (SOI) is substantially stronger when the magnetization is perpendicular to the plane compared to the in-plane direction. When the influence of SOI exceeds that of the demagnetization field, the equilibrium magnetization transitions from an in-plane to a perpendicular-to-plane.
For localized electrons in the bulk of amorphous FeB, SOI is largely independent of the magnetization direction and does not contribute to anisotropy. However, at the interface, broken symmetry along the surface normal enhances SOI when the magnetization is perpendicular to the plane, thereby increasing the magnetic energy in this orientation. This results in a competition:
The demagnetization field favors an in-plane magnetization in thicker nanomagnets, where the bulk contribution dominates.
The interfacial SOI favors an out-of-plane magnetization in thinner nanomagnets , where the interface contribution dominates.
PMA emerges only in sufficiently thin FeB nanomagnets, where the interfacial SOI dominates over the demagnetization effect.
Equation (A13) of Ref. (AIP Advance 2024) explicitly demonstrates that the anisotropy field is linearly proportional to the magnetization.
A stronger magnetization generates a higher internal magnetic field, which enhances SOI and, consequently, magnetic anisotropy. This proportionality is also experimentally observed: when the magnetization of a nanomagnet decreases or vanishes, the anisotropy field correspondingly decreases or disappears. However, in practical cases, variations in SOI strength and demagnetization effects tend to have a more significant influence on the anisotropy field than direct changes in magnetization.
 Video
Video 
| measurement of Anisotropy field. | |
|---|---|
| Conference presentation. MMM 2022 | Conference presentation. MMM 2020 |
![]()
![]() I am strongly against a fake and "highlight" research
I am strongly against a fake and "highlight" research ![]()
![]()
![]()
![]()
![]()
![]()
I will try to answer your questions as soon as possible