Dr. Vadym Zayets
v.zayets(at)gmail.com
My Research and Inventions
click here to see all content |

Dr. Vadym Zayetsv.zayets(at)gmail.com |
|
 |
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
|
Scattering Current. Spin and Charge TransportThe scattering current occurs because of changing of possition of an electron after a scattering. In the electron gas the electrons are constantly scattered from between quantum states. Because the quantum states have different coordinates in the phase space, each scattering causes an electron movement in the phase space. The scattering current can only exists when there is a difference in an electron scattering probability between two opposite directions. For example, the scattering conduction is significant in a vicinity of interface, because a substantial difference of an electron scattering probability toward and outward of the interface. The hopping conductivity, the Spin Hall effect and anomalous Hall effect occur because of a flow of the scattering current.
|
Spin/Charge Transport Equations |
 |
From the Boltzmann Transport Equations, the charge conductivity ![]() , spin conductivity
, spin conductivity ![]() , detection conductivity
, detection conductivity ![]() and injection conductivity
and injection conductivity![]() can be found
can be found
Results in short
I. The Boltzmann transport equations were solved for the scattering current
2. It was found the main required condition for a flow of scattering current:

a) current in the vicinity of the interface ======> scattering probability towards and outwards the interface is different
b) the Spin Hall effect ======> scattering probability to the left and to the right with respect of the flow direction of the drift current is different
c) hopping conductivity ======>scattering probability along the electrical field and in the opposite to the electrical field is different
3. The origin of the Spin Hall effect is explained
Scattering electron current |
Scattering hole current |
|
 |
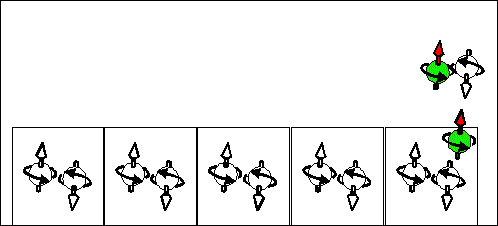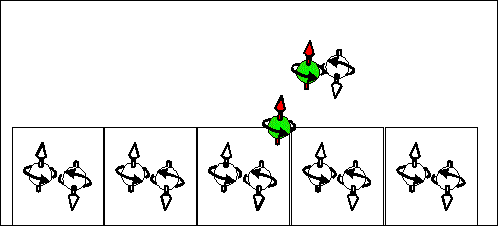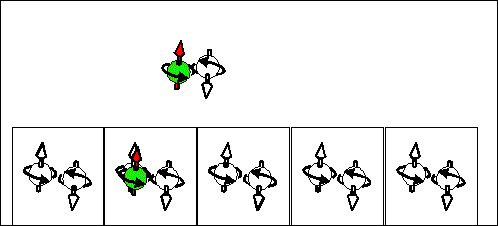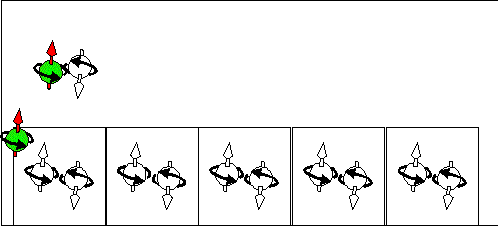
| The scattering electron current in n-type semiconductor. The yellow cells indicates quantum states. In a n-type semiconductor the most states are "empty". There are a few half-filled states. Electrons are drifted through the sample by the scattering from a half-filled state into "empty" state. At left side of the sample the directions of movement of half-filled and "empty" states are shown. At right side of the sample the directions of movement of a positive charge, a negative charge and spin are shown. The spin moves from "-" to "+". It is opposite direction to the case of p-type semiconductor | The scattering hole current in p-type semiconductor. Spin-up current. The yellow cells indicates quantum states. In a p-type semiconductor the most states are full-filled. There are a few half-filled states. Electrons are drifted through the sample by the scattering from a full-filled state into half-filled state. At left side of the sample the directions of movement of half-filled and full-filled states are shown. At right side of the sample the directions of movement of a positive charge, a negative charge and spin are shown. The spin moves from "+" to "-". It is opposite direction to the case of n-type semiconductor |
Note: The scattering current is less effective for the transport of the charge and the spin than the current of the running-wave electron .
Note: Both the running-wave electrons and the standing-wave electrons contribute to the scattering conductivity.
The running-wave-electron conduction occurs because of the electron movements between scatterings. The scattering conduction occurs because of the electron movements during scatterings. In an electron gas the electrons are constantly scattered between quantum states. Because the quantum states have different coordinates in space, each scattering causes an electron spatial movement. In the case when the electron scattering probability is the same in all directions, there is no scattering current. The scattering current can only exists when there is a difference in the electron scattering probability between two opposite directions. For example, the scattering conduction is significant in the vicinity of an interface, because of a substantial difference in the electron scattering probability toward and away from the interface. The hopping conductivity and the Spin Hall effect are examples of the scattering conductivity.
The scattering current is significantly less efficient for the spin and charge transport than the running-wave-electron current. Its contribution to the total current becomes substantial only when the current of running-wave electrons becomes small (for example, the hopping conductivity or the conductivity through a high-resistance contact (a tunnel barrier or a semiconductor-metal contact)) or when the scattering current flows perpendicularly to the current of the running-wave electrons (the Spin Hall effect).
It occurs in case when there is a difference in an electron scattering probability between two opposite directions.
The scattering conductivity is nearly zero in bulk of semiconductors and metals with a low density of defects.
The current of scattering current occurs, because of the scattering of an electron from one state to another state.
Depending between each states the scatterings occur, 3 types currents can be distinguished:
(1) Electron scattering current. half-filled + "empty" states
(2) Hole scattering current. half-filled + full-filled states
(3) full-filled / "empty"scattering current. "empty" + full-filled states & half-filled + half-filled states
Electron scattering current. half-filled + "empty" states |
Hole scattering current. half-filled + "empty" states |
full-filled / "empty"scattering current. half-filled + full-filled states & half-filled + half-filled states |
 |
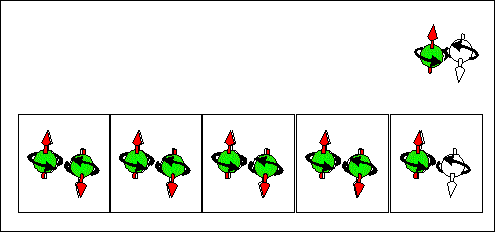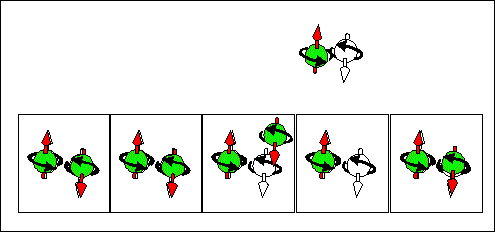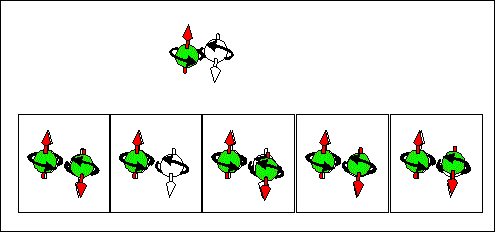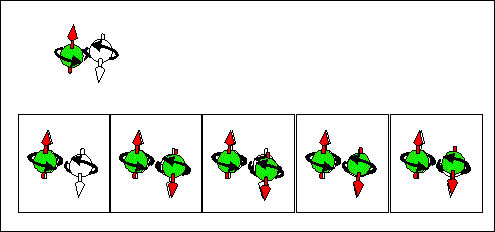 |
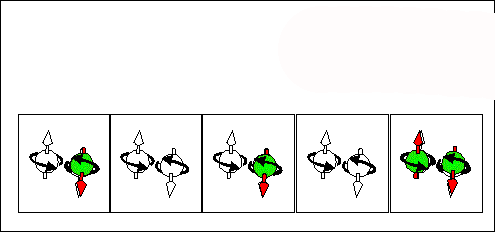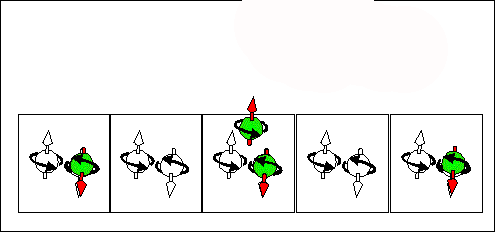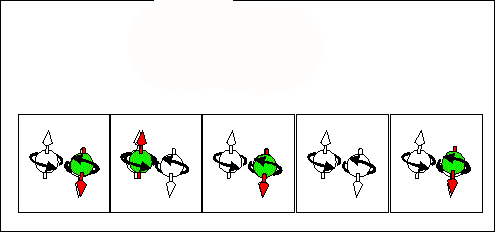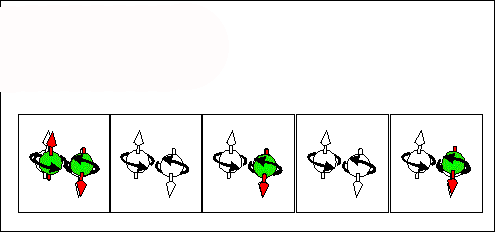 |
| Consequence scattering of an electron from a half-filled state into "empty" state corresponds to movement of half-filled states from right to left and to movement of "empty" from left to right . The spin and "-e" charge are transported in the same direction from the right to the left. | Consequence scattering of an electron from a full-filled state into a half-filled state corresponds to movement of half-filled states from right to left and to movement of full-filled from left to right. The spin and "-e" charge are transported in opposite directions. The spin is transported from the right to the left. The "-e" charge is transported from the right to the left. | Consequence scattering of an electron from a full-filled state into a "empty" state and next from a half-filled state to a half-filled state. This current does not transports the spin. It transports only the charge. |
For each current there are two contributions of different Source & destination
(1) Electron scattering current.
First contribution: source: half-filled-----> destination: "empty"; Second contribution: source: "empty"-----> destination: half-filled
(2) Hole scattering current. half-filled + "empty" states
First contribution: source: half-filled-----> destination: full-filled; Second contribution: source: full-filled-----> destination: half-filled
(3) full-filled / "empty"scattering current.
First contribution: source: full-filled-----> destination: "empty"; Second contribution: source: "empty"-----> destination: full-filled
The electron current occur because of the electron scattering between half-filled states and full-filled states. (See left figure above). Contribution: source: half-filled-----> destination: "empty";
Scattering probability is proportional to
(1) The number of states from which the electron is scattered ![]()
(2) The number of states to which the electron is scattered ![]()
(3) Overlap integral of wave functions between which the scattering occurs.
(4) Probability that the states interacts with a defect or phonon or other scattering source.
This probability may be different for a electron scattered in forward direction p_forward and electron in scattered in backward direction p_backw
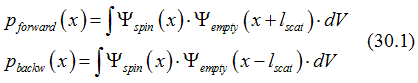
where![]() are wave functions of half-filled and "empty" states, l_scat is the average distance through which an electron moves after one scattering.
are wave functions of half-filled and "empty" states, l_scat is the average distance through which an electron moves after one scattering.
For running-wave electrons the Probability that the states interacts with a defect or phonon or other scattering source can be calculated as follows. During time dt an electron moves a distance ![]() . The mean-free path
. The mean-free path ![]() is an average distance an electron moves between scattering. The probability for electron to be scattered during time dt is
is an average distance an electron moves between scattering. The probability for electron to be scattered during time dt is
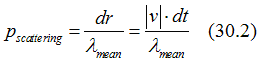
For electron current 4 scattering events should be considered
Event 1: scattering of an electron from “spin” state at position x forward to “empty” state. Because of his event, the number of spin states at point x decreases
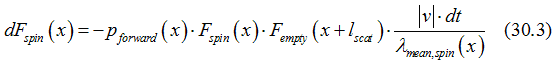
Event 2 : scattering of an electron from “spin” state at position x backward forward to “empty” state. Because of his event, the number of spin states at point x decreases
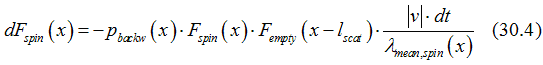
Event 3: scattering of an electron to “empty” state at position x from forward “spin” state. Because of his event, the number of spin states at point x increases
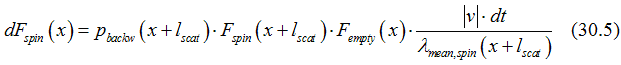
Event 4: scattering of an electron to “empty” state at position x from backward “spin” state. Because of his event, the number of spin states at point x increases
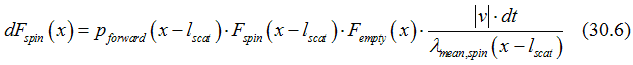
Summing up all probabilities Eqs. (30.4-30.5) under the condition that l_scat is small, we
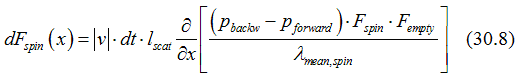
In Eq.(30.8) it is assumed that the during a scattering an electron moves along only the x-direction. In a general case the electron may move also in the y- and z-directions. It can be assumed that during a scattering, an electron moves along its propagation speed. Then, the average distance l_scat,x through which an electron moves along the x direction after one scattering is calculated as
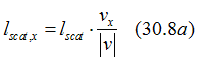
Substituting Eq. (30.8a) into Eq. (30.8) gives
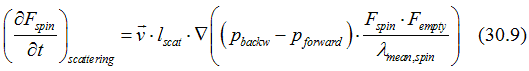
Two mechanisms of the Spin&Charge transport by Running-Wave Electrons.(1) Current of the running-wave electrons. Origin: Constant movement of electrons in a metal(2) Scattering current. Origin: electron scattering from one state to another |
 |
Blue balls represent defects. Brown ellipse shows distribution of wave function of the running-wave electrons. A scattering occurs when wave functions of two states are overlapped (shown in red color) Note: An electron current is shown. A hole current of the running wave electrons is shown here.
|
Eq. (30.9) describes the scattering when an electron is scattered from a half-filled state into an "empty". Therefore, the half-filled state is the source of the scattering and the "empty" state is the destination. Another type of the scattering can occur between a half-filled state and "empty" state. It is when "empty" state is the source and the half-filled state is the destination. It could be understood as a hole is scattered from the "empty" state to half-filled state. The second contribution can be calculating similar to Eq. (53) but replacing ![]() :
:
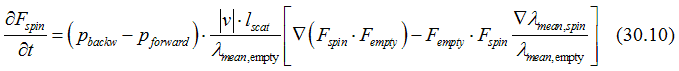
Summing up Eqs. (30.9) and (30.10) the total contribution of the scattering current can be calculated as


The Boltzmann equation Eq.(2) only with the scattering term Eq.(30.11) and relaxations term Eq(12) in a static case for half-filled states is given as
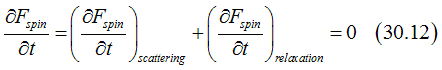
Using the approximation of a small external perturbation and substituting Eq(12) and Eq (14.4) into Eq (30.12) gives the Scattering term of the Boltzmann equation for the electron scattering current as
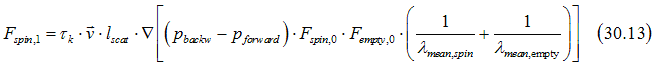
The electron scattering current can be calculated from Eq. (11.8) here as
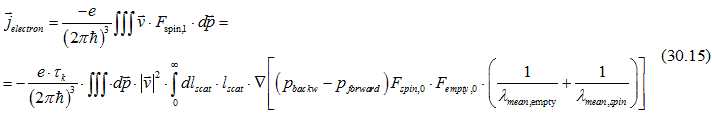
Similarly, the hole scattering current and empty/full scattering current can be calculated as
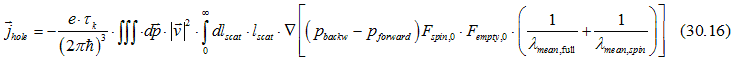
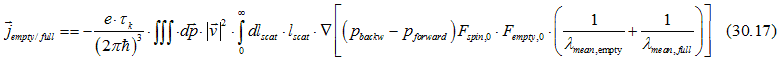
Since in the TIA assembly all spin are parallel, an electron can not be scattered between two spin states of the TIA assembly.
The probability for scattering of an electron between a half-filled state of the TIS assembly a half-filled state of the TIA assembly is 1/2.
The probability of scattering of an electron between two half-filled state, when an angle between their spin directions is theta, can be calculated as (See here)
![]()
The angle distribution of the electrons in the TIS assembly is
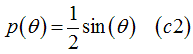
Noticing that
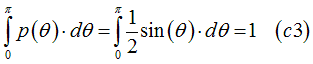
Substituting Eq.(c3) into Eq.(c1), the probability for scattering of an electron between a half-filled state of the TIS assembly a half-filled state of the TIA assembly can be calculated as
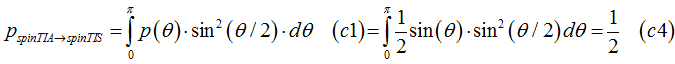
The probability for scattering of an electron between a half-filled state of the TIS assembly a half-filled state of the TIS assembly is 1/2.
Example of scattering currentSpin Hall effect difference of electron scattering probabilities along and opposite to the x-axis is due to different direction of Hso |
|
Electrons, which moves perpendicularly to the applied electrical field E, experience an effective magnetic field of spin-orbit interaction Hso. Direction of this magnetic field is different for electrons, which moves parallel and anti parallel to the x-axis. The electrons, which move along the electric field (along the y-axis) do not experience any magnetic filed of the spin-orbit interaction. The electrons may be scattered on a defect (shown as a blue ball), when wave functions of two states are overlap (shown in red). Because of the magnetic field Hso, the probability for an electron to be scattered toward and opposite to the x-xis direction are different. This causes a flow of spin current along the x-axis, when a drift current flows along y-axis. |

In order for the scattering current to flow, scattering probability in one direction should be different from the scattering probability in the opposite direction. The spin-orbit interaction makes the scattering probability different between scatterings to the the left and to the right with respect to the flow direction of the drift current.

1. The effective magnetic field of spin-orbit interaction is opposite for the electrons scattered to the left and to the right with the respect to the flow of the drift current.
2. The effective magnetic field of spin-orbit interaction is opposite for the electrons of opposite spin directions.
3. The effective magnetic field of spin-orbit interaction makes the probability
The Spin Hall effect is an example of a scattering current. The electrons, which are scattered into the left side and into the right side with respect to the flow direction of the drift current, may experience opposite direction of the effective magnetic field of the spin-orbit interaction. This may cause a different electron scattering probability to the left and right directions. The difference depends on the spin direction. This difference may cause a flow of the spin-polarized scattering current perpendicularly to the drift current. This effect is called the Spin Hall effect
I will try to answer your questions as soon as possible