Dr. Vadym Zayets
v.zayets(at)gmail.com
My Research and Inventions
click here to see all content |
Dr. Vadym Zayetsv.zayets(at)gmail.com |
|
|
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
|
Exchange InteractionSpin and Charge TransportThe exchange interaction is a fascinating effect that compels electron spins to align either parallel (ferromagnetic exchange interaction) or antiparallel (antiferromagnetic exchange interaction) or non-collinearly (Dzyaloshinskii-Moriya). Its fundamental origin lies in the spin-dependent Coulomb interaction. This intriguing phenomenon describes how two or more electrons gradually combine to form a single elementary particle, leading to a reduction in Coulomb repulsion during the process. Additionally, there exists another exchange interaction attributed to the interaction of orbital moments, rather than spins.
|
Origin of exchange interaction The exchange interaction describes the spin-dependent Coulomb interaction between electrons. The Coulomb repulsion between two electrons is smaller, when their spins are opposite, and is larger, when their spins are parallel. When two electrons of opposite spins approach each other, the breaking of time- inverse symmetry slowly disappears and system of two elementary particles transforms into a system of one particle. As a result, their mutual repulsion decreases. |
|
| The time-inverse symmetry remains unbroken for an electron state occupied by two electrons of opposite spins. This implies that the state is effectively considered as one particle without spin, carrying a charge of -2e, rather than as two separate electrons with opposite spins and charges of -e and -e. As these electrons approach each other, they gradually transform from a system of two elementary particles into a single elementary particle. Consequently, the Coulomb repulsion between them continuously decreases and eventually vanishes as they occupy the same position. |
| click on image to enlarge it |
Origin of exchange interaction |
|
| Otherwise, an infinite repulsion force would exist between these two electrons since they occupy the same spatial position, with a distance (r) between them being zero. The repulsion force is inversely proportional to the distance (~1/r^2), leading to the infinite repulsion force. |
| Two electrons literally combine to form a single elementary particle, and only in this case, there is no repulsion between them. |
The exchange interaction describes the gradual combining of two electrons into a single elementary particle and the subsequent reduction of Coulomb repulsion during this process. |
| click on image to enlarge it |
Questions & Answers
() Relation between precession damping and exchange. Spin relaxation: individual for each spin (electron) or collective for all electrons (spins) simultaneously? () Quastions about Order of orbital filling
......... 
(origin of the exchange interaction in short): Spin-dependent Coulomb interactionOrigin of exchange interaction The exchange interaction describes the spin-dependent Coulomb interaction between electrons. The Coulomb repulsion between two electrons is smaller, when their spins are opposite, and is larger, when their spins are parallel. |
|
Coulomb repulsion between two electrons as a function of angle between their spins. The density of lightning bolts indicates the strength of the Coulomb repulsion. |
| The electrostatic interaction between two electrons and how it is influenced by the mutual direction of their spins. The intensity of the electrical field is represented by lightning bolts. When the spins of the electrons are parallel, the Coulomb repulsion between them is at its maximum strength. However, when the spins are opposite, the Coulomb repulsion between the electrons significantly decreases. This decrease occurs because the electrons are in the process of merging into a single electron, for which the time- inverse symmetry is not broken and, therefore, the resulting spin is zero. As there is no interaction between different parts of a single elementary particle, the electrostatic interaction between two electrons with opposite spins becomes weaker. |
| click on image to enlarge it |
(The reason, why the Coulomb interaction is spin- dependent): When two electrons of opposite spins occupy one single quantum state, the time- inverse symmetry becomes unbroken and two electrons literally become one single new particle with charge of -2e and no spin. 
(Why broking and unbreaking symmetry is important for the exchange interaction): The primary object of our Universe are Quantum Fields (the Electromagnetic field, the Quantum Field of Electrons, the Quantum field of Quarks etc), but not particles (an electron, an photon, a quark). A particle is just a stable quantum state of a specific quantum field. (see more details here).
When certain symmetries of space/time are broken or restored, it can lead to the creation or annihilation of new particles, alterations in existing particle properties, or changes in specific particle attributes.
s 
s 
(fact): The exchange interaction describes the gradual combining of two electrons into a single elementary particle and the subsequent reduction of Coulomb repulsion during this process.For an electron with the spin, the time-inverse symmetry is broken, resulting in a spinor wavefunction for the electron. In the case when two electrons with opposite spins occupy a single quantum state, they become one single new particle with charge of -2e and no spin. Notably, the time-inverse symmetry for this newly formed particle becomes unbroken, and its wavefunction takes on a simpler scalar form as representing one particle.
It's important to emphasize that this composite particle is not merely a straightforward summation of two individual electrons with opposite spins. In a simple superposition of two such electrons, the time-inverse symmetry remains broken. However, in this double-occupied state, the time-inverse symmetry becomes unbroken. It means that even though it is known that the quantum state is occupied by two electrons of opposite spins, but, the specific orientation in which these opposing spins are aligned remains undetermined. It is unknown and fundamentally undefined whether two opposite spins are aligned upwards and downwards, left and right, or front and back.
Furthermore, it's crucial to note that there is no Coulomb repulsion or any form of interaction between these two electrons within this composite particle. Therefore, the quantum state occupied by these two electrons with opposite spins isn't simply a combination of two separate particles situated in the same location. Instead, it genuinely constitutes a new and distinct particle entity.
(Why is there no Coulomb repulsion between two electrons of opposite spins occupying one quantum state?): Two electrons combine and become a single elementary particle. An elementary particle does not have parts. Therefore, there can not be any interaction between nonexistent parts of elementary particle. That is why the Coulomb interaction between two electrons of opposite spins is switched off when they occupy one state. 
(symmetrical and asymmetrical wavefunction for a description of the exchange interaction)
:The symmetrical and asymmetrical wavefunction, which are used to describe the exchange interaction, just describe the process how two individual particles are gradually transformed into one particle as two electrons approach each other.
How is it possible that two particles become one particle?
An object is distinguished from vacuum when at least one symmetry of the space/ time is broken for this object. Two particles are distinguished from each other and can be considered as two separate objects when they can be distinguished at least by one different feature meaning at least one broken symmetry is different for those two objects. (see here for more details)
Origin of exchange interaction The exchange interaction describes the spin-dependent Coulomb interaction between electrons. The Coulomb repulsion between two electrons is smaller, when their spins are opposite, and is larger, when their spins are parallel. When two electrons of opposite spins approach each other, the breaking of time- inverse symmetry slowly disappears and system of two elementary particles transforms into a system of one particle. As a result, their mutual repulsion decreases. |
|||||||||
Coulomb interaction vs. distance between electrons |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
| Coulomb repulsion between two electrons as a function of distance between them. The density of lightning bolts indicates the strength of the Coulomb repulsion. | |||||||||
The electrostatic interaction between two electrons and how it is influenced by the distance between electrons and the mutual direction of their spins. The intensity of the electrical field is represented by lightning bolts. When the spins of the electrons are parallel, the Coulomb repulsion between them is at its maximum strength. However, when the spins are opposite, the Coulomb repulsion between the electrons significantly decreases. This decrease occurs because the electrons are in the process of merging into a single electron, for which the time- inverse symmetry is not broken and, therefore, the resulting spin is zero. As there is no interaction between different parts of a single elementary particle, the electrostatic interaction between two electrons with opposite spins becomes weaker. |
|||||||||
(note): An elementary particle or an object exists only when at least one of many vacuum symmetries are broken for this objects. (see here for more details) |
|||||||||
(note) :The distinction between one elementary particle and two elementary particles lies in the fact that, in the case of two particles, each one can be differentiated based on differences of at least one broken symmetry (e.g. a spatial position or spin or electrical charge). |
|||||||||
| click on image to enlarge it |
Establishing foundation & building blocks: elementary particles.
The building blocks of the standard model are elementary particles. All physics within the standard model arises from interactions between these elementary particles. While elementary particles can transform into one another, it is of utmost importance for the standard model's foundation that these elementary particles, as the fundamental building blocks, remain unchanged, preserving their core properties.
Establishing foundation & building blocks: quantum fields or fields of the different symmetries of the space- time
In the post-standard model, the establishment of a foundation and building blocks are quantum fields or fields associated with different space-time symmetries. The basic components of the post-standard model consist of quantum fields representing various broken or unbroken states of space-time symmetries. An elementary particle in the post-standard model is essentially a stable state resulting from the breaking of several symmetries. The properties of an elementary particle do not remain unchanged; they depend on the surrounding environment.
What is the issue with the standard model in describing the exchange interaction?The core fundamentals of the standard theory involve elementary particles with unchanging properties, directly conflicting with the inherent nature of the exchange interaction. The exchange interaction elucidates a process where two or more particles progressively merge to create an entirely distinct elementary particle. The foundation of the exchange interaction lies in the mechanism of non-conservation of elementary particle properties, contradicting the fundamental principle of the standard model, which firmly asserts the full conservation of all properties of the elementary particles.
The best shot for the standard model to describe the exchange interaction. Symmetrical and asymmetrical wavefunctions.
The nature of the exchange interaction fundamentally contradicts the basic tenets of the standard model. How, then, does the standard model reconcile with the exchange interaction?
It employs a trick— essentially acknowledging the unavoidable reality of the gradual conversion of elementary particles into one different elementary particle while hiding the contradiction in complex details.. The method involves using an antisymmetric or symmetric combination of product wave functions in position space. In this approach, the wavefunction for each elementary particle, such as an electron, remains unchanged, but the sum and difference of these wavefunctions are employed to represent new particles.
Taking the example of an electron, the sum eventually forms a new elementary particle with a charge of -2e, while the difference essentially disappears. Consequently, two electrons with opposite spins gradually transform into a single elementary particle with no spin and a charge of -2e. This trick aligns well with the realistic scenario where combining two electrons with broken time-inverse symmetry results in one elementary particle with a charge of -2e and unbroken time-inverse symmetry.
Therefore, this method, utilizing symmetrical and asymmetrical wavefunctions, effectively mimics a fundamental and universal property of any quantum field, which is known as the exchange interaction.
Principle of undistinguished electrons (incorrect):
In a group of electrons, individual electrons cannot be numbered or distinguished, implying that nothing changes if two electrons swap their positions. Consequently, the Hamiltonian for a group of interacting electrons should exhibit symmetry when their positions are interchanged. This principle is also known as the principle of identical particles (See wiki here)
This principle can be satisfied by employing either an antisymmetric or symmetric combination of product wave functions for individual electrons in position space.
The reason why the principle of undistinguished (identical) particles is incorrect::
In the post-standard model, each elementary particle (e.g., an electron) corresponds to a stable state of various broken symmetries of space/time. Two elementary particles are distinguished from each other and, therefore, interact with each other (e.g., Coulomb repulsion, gravitational attraction) only if the specifics of at least one broken symmetry are different for each particle. For example, the first particle has spin up, and the second particle has spin down. When all broken symmetries are fully identical for two particles, the two particles literally transform into one single particle, and any interaction between these two particles ceases to exist.
The two elementary particles with different spatial coordinates have the special-position-transfer symmetry broken differently. As a result, they are two clearly distinguished particles with various interactions between them. The case of two particles with different spatial coordinates is not fundamentally different from the cases of two particles with different energy, spins, or charges. Therefore, the wavefunctions of those two particles should not be mixed up. Otherwise, the wavefunctions of all existing elementary particles with different energy, spin, momentum, and charge would be mixed up, leading to an absurd jumble.
Why there are different types of the exchange interaction?The exchange interaction describes the process of converting two electrons into one particle when they come close together. Initially, these electrons with opposite spins are described by relatively simple and nearly identical wave functions when they are far apart. However, as their distance diminishes, they undergo a partial conversion into a single particle. Although they still remain two distinct entities, they exhibit unique properties different from those at a greater distance. This conversion is governed by both symmetric and antisymmetric components of their shared wave function. During this intriguing transformation, the Coulomb interaction between the modified electrons and their surrounding environment is characterized by various types of the exchange interaction. This complex phenomenon sheds light on the interplay between quantum properties as electrons approach and interact with one another.
There are 3 major types to the exchange interaction:
| Origins of exchange interaction | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
Origin of First Type/Contribution for the exchange interaction:Its origin is explained as followed: Two electrons of opposite spins may occupy one quantum state. It literally means that in the case when the spins are opposite there is no Coulomb's repulsion between electrons. In contrary, when spin are parallel, the Coulomb's repulsion between electrons is very strong. It means that at very short distance the Coulomb's repulsion between electrons strongly depends on their spin directions. The Coulomb's interaction between electrons at a short distance forces the electron spins to align antiparallel.
A single elementary particle does not have parts and it can not interact with itself The picture shows what would happen if an electron could interact with itself. Since there is no holding force between parts of an electron, the repelling Coulomb's force would blow up the electron. |
|
| click on image to enlarge it |
Fig.2. Coulomb repulsion energy between two electrons as function of distance between them click here to enlarge |
|
For longer distances, the repulsion energy is reverse proportional to distance between electrons E~1/x and it is spin-independent. For shorter distance, the energy is spin dependent. In the case of the opposite spins (blue line), the repulsion vanishes at shorter distances. In the case of the parallel spins (red line), the repulsion become infinitely large at shorter distances |
Q. Protons are fermions. Similar to electrons, can two protons of opposite spins occupy one quantum state?Q. The electron might be a point-like particle with infinitely small size. Therefore, the Coulomb interaction inside the electron has no meaning?Q. Proton has the charge radius, which could be measured experimentally. Does electron has the charge radius.
Fig.3. Two electrons of opposite spins, when combined, form an elementary particle without spin. Each quantum state can be occupied by two electrons of opposite spins. When a quantum state is occupied by one electron, it is an elementary particle with charge -e and spin=1/2 When a quantum state is occupied by two electrons, it is an elementary particle with charge -2e and spin=0 click here to enlarge |
|
Origin of Second Contribution for the exchange interaction:Its origin is explained as follows: Due to fermion nature of an electron, the wave function of two electrons is symmetrical, when spin are antiparallel, and the wave function is antisymmetric, when spin are parallel. When two localized electrons are located at two neighbor atoms, antisymmetric wave functions means that probability to find electrons is smaller at point, which is between atoms, than at point in the vicinity of nucleus. In contrast, symmetrical wave functions means that probability to find electrons is nearly the same between atom and in the vicinity of nucleus. Therefore, when spins are parallel, the probability for an electron be at vicinity of nucleus is larger and the absolute value of the negative nucleus-electron interaction energy becomes larger comparing to the case of the antiparallel spins. It forces the spins to align ferromagnetically.Fig.4. Wavefunction of a system of two electrons in the vicinity of two nuclei. Imaginary case of electron as only a particle, not a wave Each electron is distributed around one nucleus. There is an overlap of electron wavefunction in the middle click here to enlarge |
|
Fig.5 Wavefunction of a system of two electrons in the vicinity of two nuclei. Imaginary case of electron as only a wave, not a particle There is no any difference between electron 1 and electron 2. Their wave functions are exactly the same. click here to enlarge |
|
Fig.6 Probability to find one electron at coordinate x1 and second electron at coordinate x2 of a system of two electrons in the vicinity of two nuclei. Realistic case when electrons have properties of both a wave and a particle Animation parameter: Distance between two nuclei. Black balls show the positions of nuclei. |
||||
|
Fig.7 (left) Probability to find one electron at coordinate x1 and second electron at coordinate x2=-x1-d, where d is distance between nuclei. (right) Coulomb attraction energy between electrons and nucleus as function of distance between nuclei. Animation parameter: Distance between two nuclei. Black balls show the positions of nuclei. click here to enlarge |
|
Comparison between different representation of an electron Probability of one electron to be at point x1 and second electron at point x2 black balls show position of nuclei |
||||||
|---|---|---|---|---|---|---|
|
Origin of Third Contribution for the exchange interactionIts origin is explained as follows: Due to fermion nature of an electron, the wave function of two electrons is symmetrical, when spin are antiparallel, and the wave function is antisymmetric, when spin are parallel. The Coulomb's repulsion between electrons is smaller when a distance between electrons is longer. In the case of antisymmetric wave function (parallel spins) the average distance between two electrons is a little bit longer (red line of Fig. 7 ) than for the case of symmetric wave function (antiparallel spins) (blue line of Fig. 7 ) . Therefore, the Coulomb's repulsion energy is smaller parallel spins. It forces the spins to align ferromagnetically.Bethe–Slater curve It is empirical curve, which represents the measured exchange interaction as distance between localized electrons. |
|
Since the exchange interaction directly depends on the electron spin, the exchange interaction of electron with all surrounding electrons can be represented as the effective magnetic field Hexchange, which interacts with the electron spin.Effective magnetic field of exchange interaction Hexchange |
|---|
 |
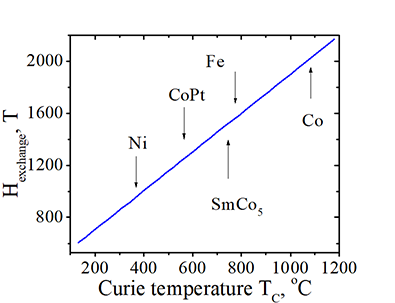Fig. 51 The effective magnetic field Hexchange of the exchange interaction, which an electron experiences from all neighbor electrons vs. material Curie temperature. |
(fact) At Tc the thermal fluctuations breaks exchange alignment of neighbor electrons. Therefore, the electron thermal energy becomes larger than the energy of the exchange interaction. |
| See more detailed explanation here |
| click on image to enlarge it |
The exchange interaction is poorly described by the magnetic field Hexchange. the magnetic field Hexchange is just only a representation, but Hexchange is not a real magnetic field
The Hexchange can be evaluated from the Curie temperature of a ferromagnetic material.
The representation of the exchange interaction by the magnetic field Hexchange can be both helpful and confusing
The Hexchange is about 1000-2000 T. It is much bigger than the field, which can be achieved by any known magnet. For example, the largest magnetic field achieved by an electromagnet is about 1 T and by a superconductive magnet is about 30 T. Since is just a representation of the exchange interaction, but is not a real magnetic field. The huge value of Hexchange has a little physical meaning. Why is the exchange interaction so strong?
The core of the exchange interaction lies in the modulation, and even toggling, of Coulomb repulsion. Given the substantial strength of the Coulomb repulsion force, the exchange interaction also gains considerable potency.
3 types of magnetic field |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||
| The spin properties of electrons are exactly the same for each type of the magnetic field. In an equilibrium the electron spin is aligned along the total magnetic field, which is a vector sum of all three types of the magnetic field. There is a spin precession before the alignment. | ||||||||||||
| click on image to enlarge it |
Exchange interaction is not about interaction between spins. Exchange interaction is about the interaction between parts of a broken symmetry. |
|---|
When two particles are distinguished only by their different parts of the same bro |
The spin describes the breaking of the most simplest symmetry, which is the time-inverse symmetry. This broken symmetry has only two parts, which is described by the spin-up and the spin-down states. As a result, the exchange interaction between two particles of a different spin is the simplest one and most- known and understood. |
| The orbital moment describes the breaking of the rotation symmetry and, therefore, the exchange interaction between particles of a different orbital moment is possible, but it is more complex and rare. It is because the rotation symmetry is more complex. For example, p-symmetry is broken into 3 components (but not 2 components as in the case of the spin). As a result, the conditions between these 3 components and conditions for the unbreaking of the p-type rotational symmetry are complex. That is why the exchange interaction between particles of a different orbital moment is very rare. |
| click on image to enlarge it |
(important fact): Significant exchange interaction occurs exclusively between two highly similar electrons. In order for the exchange interaction to be substantial, the properties of both electrons should closely match. This includes factors such as electron size, orbital moment, spatial symmetry, and velocity. As the parameters of the two electrons diverge, the exchange interaction weakens accordingly. The greater the differences between the electron properties, the less pronounced the exchange interaction becomes.
(reason) : The exchange interaction refers to the phenomenon where the Coulomb interaction and other interactions between two particles are diminished as they combine into a single particle, restoring a previously broken symmetry, often the time-inverse symmetry. However, this merging process is restricted to fully identical particles. The greater the differences between two particles, the weaker the exchange interaction becomes.
| the exchange interaction between two conduction electrons is rather weak. |
| the exchange interaction between a conduction electron and a localized electron is rather weak |
(imprtant fact:): In a solid, the exchange interaction is strongest between localized electrons.
Does the exchange interaction exist between the electron and the proton?
No, there is no exchange interaction between the proton and the electron due to their fundamental differences as particles. Each of them possesses distinct broken symmetries that are unique to their nature. The proton and the electron just are two very different particles possessing very different broken symmetries.
Does the exchange interaction exist between a conduction electron and a localized electron?
Yes. However, the exchange interaction between a conduction electron and a localized electron is rather weak, because of many of substantial differences between a conduction and a localized electron.
Differences which make the exchange interaction between a conduction electron and a localized electron weak:
(difference 1): size 
The size of a localized electron is about 0.1 nm (about interatomic distance)
The size of a conduction electron is about 10 nm -1000 nm (it equals to the mean- free path and depends on the crystal quality. See here)
(difference 2): orbital moment 
Orbital moment of a localized electron is quenched, which means it is zero. (see here)
Orbital moment of a conduction electron is unquenched
| The exchange interaction refers to the phenomenon where the Coulomb interaction and other interactions between two particles are diminished as they combine into a single particle, restoring a previously broken symmetry, often the time-inverse symmetry. However, this merging process is restricted to fully identical particles. Discrepancies in electron size, orbital moment, spatial symmetry, or velocity between two electrons makes the merging process more difficult, resulting in a weaker exchange interaction. |
(difference 3): orbital symmetry 
Orbital symmetry of a localized electron is d- type or f- type.
Orbital symmetry of a conduction electron is s- type or p- type
(difference 4): movement 
a localized electron is stationary
a conduction electron moves
(difference 5): scattering time (life time)
Scattering of a localized electron is rare. Each localized electron is scattered each ~ 1 millisecond
Scattering of conduction electrons is frequent. Each conduction electron is scattered each 10-100 femtosecond
Group of spin-polarized conduction electrons |
Group of spin-unpolarized conduction electrons | |
|---|---|---|
 |
 |
|
| Spins of all electrons are in one direction. Click on image to enlarge it. | Spin directions are equally distributed in all directions. . Click on image to enlarge it. |
Does the exchange interaction exist between two conduction electrons?
Yes. However, the exchange interaction between two conduction electrons is rather weak.
(reason):
The exchange interaction is significant only between two very similar and nearly-identical electrons. However, the conduction electrons differ greatly from each other primarily due to their frequent scatterings. Each conduction electron occupies a quantum state for only around 10 femtoseconds before scattering into another state. This distinct time continuity symmetry for each conduction electron almost nullifies any potential exchange interaction. Moreover, each conduction electron moves in a different direction with slightly varying speeds. Unlike localized electrons whose orbital moment is quenched, the orbital moment of a conduction electron is not quenched and differs for each electron. All these dissimilarities make it nearly improbable for two conduction electrons to form a pair that unbreaks the broken time-inverse symmetry and results in a sizable exchange interaction.
(fact): Frequent electron scattering aligns the spins of the spin-polarized conduction electron and establishes the spin distribution of the conduction electrons. The exchange interaction does not play a role in influencing the spin alignment of the conduction electrons.
Two groups of conduction electrons:
(group 1): Spin- unpolarized conduction electrons.
Their spins are distributed equally in all directions. This group exists in both the ferromagnetic and non-magnetic metals.
(group 2): Spin- polarized conduction electrons.
Their spins are aligned in one direction. This group exists in a ferromagnetic magnetic metal and can be injected into a non-magnetic metal.
See more details here and here
Approximated Hamiltonian for Exchange interaction. Heisenberg Hamiltonian |
 |
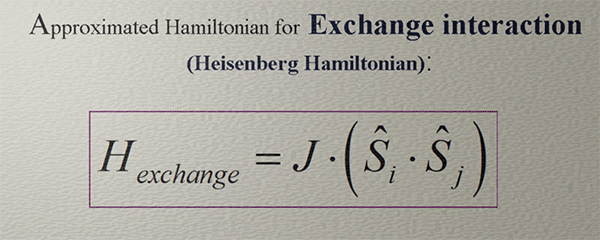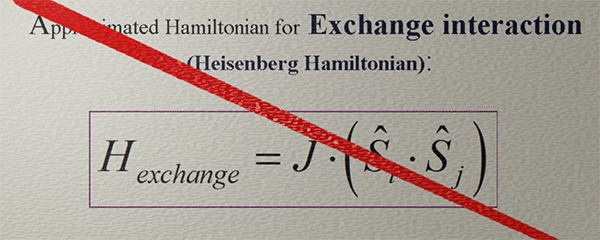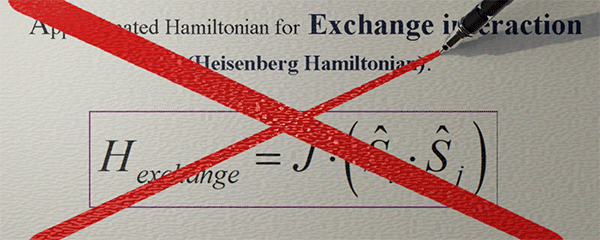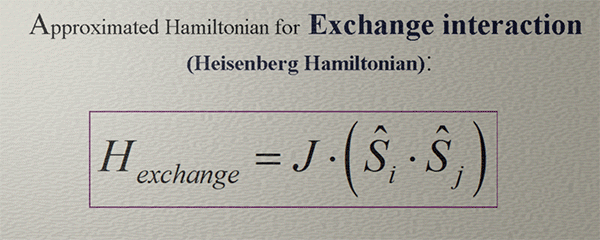| (note) This Hamiltonian captures only a very general tendency that two spins can interact in either an antiferromagnetic manner, where their spins are forced to align antiparallel to each other, or in a ferromagnetic manner, where their spins their spins are forced to align parallel each other. |
| In fact,, the exchange interaction exhibits a remarkable complexity, richness, and intrigue. It encompasses the intricate phenomenon of the Coulomb interaction diminishing in strength when the broken time-inverse symmetry is modulated in relation to the mutual spins and positions of two or more electrons. This intricate interplay adds depth and fascination to the exchange interaction. |
| click on image to enlarge it |
In the majority of cases, the exchange interaction aligns spins either parallel or antiparallel to each other, resulting in minimum or maximum exchange energy for parallel or antiparallel alignments.. The simplest mathematical representation for such behavior is the product of two vectors. As a result, the Hamiltonian of the exchange interaction is expressed as a vector product of two spins:
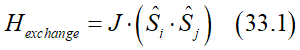
where J is the exchange constant.
(note): Eq. (33.1) can be obtained from an antisymmetric combination of the product wave functions two interacting electrons (See here)
(fact): While the oversimplified description in Eq.(33.1) may yield correct results in many cases, the exchange interaction exhibits a more diverse, intriguing, rich and complex nature.
The cases when the oversimplified description in Eq.(33.1) is not valid:
(case 1): Exchange interaction between 3 or more electrons.
The fundamental origin of the exchange interaction lies in the restoration of broken time-inverse symmetry within a pair of electrons. However, when three or more electrons interact, multiple possibilities arise for an electron to form pairs with electrons of opposite spins. Consequently, there is a competition between different pairs.
One electron has one broken time-inverse symmetry, which can be unbroken in one pair. Competition with many pairs substantially diminishes the existing exchange interaction within one pair. Additional exchange interactions with more electrons substantially diminish the existing exchange interaction within one pair. This significant reduction of exchange interaction in multi-pair electron scenarios is not accounted for by Eq.(33.1).
(case 2): Non-collinear Exchange interaction ( Dzyaloshinskii–Moriya exchange interaction).
When three electrons interact simultaneously, and each pair exhibits antiferromagnetic exchange interaction, their spins align in a non-collinear manner. For instance, if electron 1 and 2 are aligned antiparallel, the antiparallel alignment of electron 3 with either electron 1 or 2 results in parallel alignment with the other electron. This configuration is energetically unfavorable compared to a non-collinear alignment. This effect is not accounted for by Eq.(33.1).
 |
| (fact): The most straightforward approach is not always the most accurate. |
How does the exchange interaction, which is inherently antiferromagnetic for two electrons and cannot change to ferromagnetic , lead to the establishment of ferromagnetic order in ferromagnetic metals like Fe, Co, or Ni?
Origin of ferromagnetic exchange interaction |
 |
| The ferromagnetic exchange interaction between two electrons in the presence of their neighboring nuclei. The density of white lightning bolts represents the strength of Coulomb repulsion between the electrons, while the density of red lightning bolts signifies the strength of Coulomb attraction between an electron and a nucleus. The insets illustrate the positive repulsion energy (-e/-e) between the two electrons, the negative attraction energy (+p/-e) between an electron and a nucleus, and the total negative energy resulting from the sum of all these interactions. |
| (when spin direction between electrons changes from antiparallel to parallel): (effect 1) The Coulomb repulsion between two electrons becomes larger and restores to its full strength-> (consequent effect 2) The stronger repulsion pushes the two electrons further from each other -> (consequent effect 3) As each electron is pushed closer to its nucleus, the attractive energy between the nucleus and the electron increases. |
| The total energy of all interactions decreases for parallel spins making the ferromagnetic alignment energy- favorable. Even though the ferromagnetic alignment leads to the stronger repulsion between two electrons and, therefore, the larger positive repulsion energy, the increase of the negative energy of the attraction between the nucleus and the electron causes the total energy to decrease. |
| (note) The Coulomb interaction between the electrons and nucleuses is spin- independent. Only the Coulomb repulsion between the two electrons depends on their spin mutual directions. |
| click on image to enlarge it |
It is because the alteration of the Coulomb repulsion between two electrons leads to a change of the spatial position of the electrons or, the same, the spatial distribution of the electrons. It affects the interaction of the electrons with other particles. Particularly, it affects the Coulomb attraction of the electrons with atomic nucleuses. The parallel alignment of the spins leads to a stronger repulsion between two neighboring electrons and, as a result, pushes the electrons away from each other and, therefore, closer to the neighboring nucleus strengthening the attraction Coulomb force between an electron and a nucleus. As a result, negative attraction energy between electrons and nucleuses increases, compensating for an increase of a positive repulsion energy between the two electrons and leading to a decrease in the total energy. Therefore, the parallel spin alignment becomes energy favorable.
Facts, which cannot be changed under any circumstances, :
(unchangeable fact 1) The exchange interaction between two electrons in vacuum is always antiferromagnetic.
(unchangeable fact 2) The Coulomb repulsion between two electrons is smaller when their spins are antiparallel and is larger when their spins are parallel. As a consequence, the positive energy of their repulsion is smaller in the case when spins are parallel than in the case when spins are antiparallel.
(unchangeable fact 3) The distance between two electrons is always shorter when their spins are parallel and is longer when their spins are antiparallel.
(essential key for exchange interaction in a solid): Coulomb interaction between an electron and nucleusThe spin-independent Coulomb attraction interaction between an electron and a nucleus plays a crucial role as the essential key for exchange interaction in a solid.
(fact) The Coulomb interaction between the electrons and nucleuses is spin- independent. Only the Coulomb repulsion between the two electrons depends on their spin mutual directions.
(essential key for exchange interaction in a solid): Spin-dependent modulation of electron position and electron distributionWhile the exchange interaction's fundamental property involves spin-dependent modulation of Coulomb repulsion energy between electrons, the electron position change resulting from this repulsion modulation has a more significant impact on the exchange interaction in a solid.
(fact: total energy) The equilibrium spin alignment corresponds to the state of minimum total energy for the whole solid, which is a sum of a positive electron-electron repulsion energy and a negative electron- nucleus attraction energy.
(fact: weak modulation of repulsion energy between electrons as the spins rotates) Although the Coulomb repulsion regains its full strength when spins between two electrons align in parallel, the increase in positive repulsion energy is not very significant. This is because the stronger repulsion force pushes the electrons away from each other. As the distance r between electrons increases, the repulsion energy decreases as 1/r. Consequently, the gain in repulsion energy for the parallel spins is partly compensated by the increased distance between electrons.
(fact: strong modulation of attraction energy between electron and nucleus as spins rotates) The additional repulsive force exerted by neighboring electrons pushes an electron closer to the nucleus, leading to an increase in the negative attraction energy between the electron and the nucleus. This pushing effect is stronger when the spins between electrons are parallel. The substantial gain in attractive energy for parallel spins is significant because it varies inversely with the distance between the electron and nucleus. This gain in energy defines the ferromagnetic exchange interaction and establishes the ferromagnetic spin order within the solid.
Origin of ferromagnetic exchange interaction. Spin- dependent shift of electron position as a key factor of exchange interaction in a solid. |
|---|
 |
| The ferromagnetic exchange interaction between two electrons in the presence of their neighboring nuclei. The density of white lightning bolts represents the strength of Coulomb repulsion between the electrons, while the density of red lightning bolts signifies the strength of Coulomb attraction between an electron and a nucleus. Twigs show the distance between electron and nucleus. |
| The Coulomb repulsion between electrons depends on the spin angle. When the spins are parallel, the Coulomb repulsion becomes stronger and pushes the electrons further away from each other. As a result, the electrons are shifted closer to the nucleuses. When the spins are antiparallel, the Coulomb repulsion becomes weaker, the electrons are shifted closer to each other and away from the nucleuses. |
(fact:) The shifts of the electrons positions mainly define the total energy of all interactions and, therefore, the polarity of the exchange interaction. |
| click on image to enlarge it |
Origin of ferromagnetic exchange interaction. Orbital modification accordingly to spin arrangement. |
|---|
 |
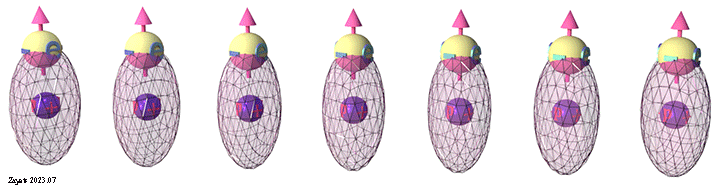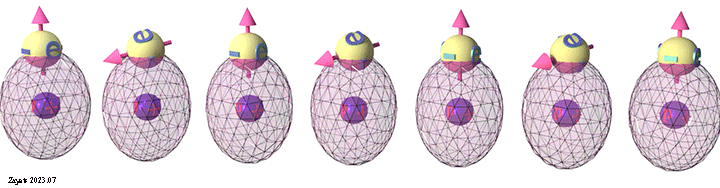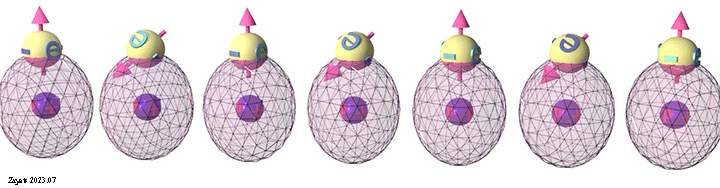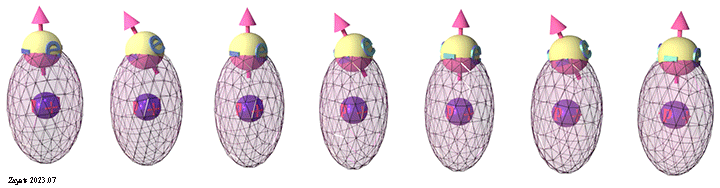| Schematic diagram shows modification of the orbital electron distribution according to spin arrangement between neighboring atoms. Blue balls show the atomic nucleuses. The spheres show the schematic electron distribution in an atomic orbital. |
| (ferromagnetic spin arrangement): When neighboring spins are in the same direction, the Coulomb repulsion between electrons strengthens, causing the orbitals to deform and draw closer to the nuclei. This intensifies the negative attraction energy between the electron and nucleus. Consequently, the total energy for the parallel spin arrangement becomes smaller, making the ferromagnetic spin arrangement energetically favorable. |
(antiferromagnetic spin arrangement): When neighboring spins are in opposite directions, the Coulomb repulsion between electrons diminishes, leading the orbitals to relax into their undisturbed spherical shape, positioning them further away from the nucleus. As a consequence, the negative attraction energy between the electron and nucleus weakens. Accordingly, the total energy for the antiparallel spin arrangement increases, making the antiferromagnetic spin arrangement energetically unfavorable. |
| click on image to enlarge it |
As the distance between electrons or atoms in a crystal lattice varies, the contributions to the exchange interaction from electron-electron (-e/-e) and electron-nuclear interactions (+p/-e) also change. Since the electron-nuclear contribution (+p/-e) is ferromagnetic and the electron-electron contribution (-e/-e) is antiferromagnetic, the polarity of the exchange interaction can shift, transitioning, for instance, from ferromagnetic to antiferromagnetic and then back to ferromagnetic as the distance between electrons increases.
(note) Such a change of the polarity of the exchange interaction also can be described by the exchange integral J (the exchange constant).
By introducing a layer of a different material between two ferromagnetic layers, the polarity of the exchange interaction between the layers may oscillate between ferromagnetic and antiferromagnetic types with the addition of each atomic layer of the inserted material.
It is the case when the both exchange interaction between electrons of ferro and insertion layers and between electrons of different insertion layers is antiferromagnetic.
Spin direction in each layer:
(one insertion layer): ferromagnetic: (ferro) <->(1st)<->(ferro)
(two insertion layers): antiferromagnetic: (ferro) <->(1st)<->(2nd) <->(ferro)
(three insertion layers): ferromagnetic: (ferro) <->(1st)<->(2nd) <->(3rd) <->(ferro)
(four insertion layers):antiferromagnetic: (ferro) <->(1st)<->(2nd) <->(3rd) <->(4th) <->(ferro)
Interlayer exchange coupling |
 |
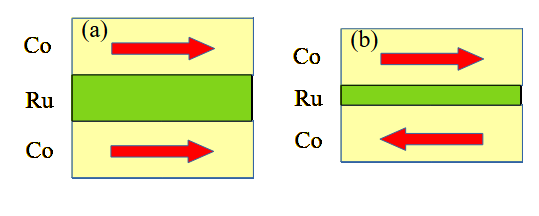| click on image to enlarge it |
Interlayer exchange coupling is employed to alter the polarity of the exchange interaction between two layers, transitioning it from ferromagnetic to antiferromagnetic. To achieve this, a non-magnetic layer of one or two monolayers is inserted between two ferromagnetic layers.
How to measure the strength of the Interlayer exchange coupling?
An external magnetic field is applied along the magnetic easy axis, and the magnetization of the sample is measured. In the antiferromagnetic alignment case, the magnetization is almost zero, whereas in the ferromagnetic alignment case, the magnetization is significant. There is a step rise of the magnetization at the magnetic field Hex that overpowers the interlayer exchange interaction and induces the transition from antiferromagnetic to ferromagnetic alignment. This magnetic field Hex determines the strength of the Interlayer exchange coupling.
Applications of the interlayer exchange coupling:
(application 1): pinning of the "pin" layer
A material with weak magnetic anisotropy becomes firmly fixed to a material with strong magnetic anisotropy due to the exchange interaction. Consequently, the magnetization of the material remains firmly aligned along the easy axis and does not deviate from it even under a moderate magnetic field.
Polarity of the exchange: ferromagnetic. Non- magnetic layer is not used.
(application 2): magnetic layer with no net magnetization
A layer with a net magnetization of zero does not generate a magnetic field, thus having no impact on its surroundings. For instance, the reversal of magnetization in such a layer within an MRAM cell (a recording event) does not trigger the magnetization reversal in neighboring MRAM cells.
Polarity of the exchange: antiferromagnetic. Thickness of a spacer ~ 0.5 nm.
Features of the interlayer exchange coupling:
(feature 1): interlayer exchange coupling is weak
A spacer layer of a very different material is inserted, which electrons have a different symmetry, size and etc. The exchange interaction is strong only between very similar electrons.
(feature 2): The spins of non- magnetic material becomes aligned.
It is due to the proximity effect (see above)
(feature 3): The space layer changes the polarity interlayer exchange coupling to antiferromagnetic.
This implies that there is no ferromagnetic contribution due to the spin-dependent shift of the electron position and the modulation of the Coulomb interaction between the electron and nucleus.
The reason behind this is the utilization of a heavy metal as a spacer material, where the outer shell electrons are relatively distant from the nucleus and well shielded by inner shell electrons. As a result, the spatial shift has minimal impact on their Coulomb interaction with the nucleus.
| Antiferromagnetic exchange coupling using Ru & Ir spacers | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
| (sample): (Fe/Pt): spacer: (Fe/Pt). There is either Ru or Ir spacer between two Fe/Pt multi layers. Equilibrium magnetization is perpendicular to the plane. In equilibrium the magnetization of the (Fe/Pt) layer is aligned antiparallel (AF) with respect to | |||||||||
 Yakushiji, et.al. Appl. Phys. Express 8 083003 (2015) Yakushiji, et.al. Appl. Phys. Lett. ; 110 (9): 092406 (2017) |
|||||||||
| research was done by K. Yakushiji, AIST | |||||||||
| click on image to enlarge it |
As you previously mentioned, the magnetic field of the exchange interaction is remarkably strong, approximately 1000 Tesla (refer to Fig. 51 above). However, the actual measured magnetic field of the exchange interaction is significantly smaller. According to the data from Fig. 47, the magnetic field of the exchange interaction is only Hex=14 kGauss=1.4 Tesla. What could be the reason for this discrepancy?
(reason 1) Measured magnetic field of the exchange interaction is much larger than Hex
The external magnetic field influences all atomic layers within the antiferromagnetically coupled layer, while the interlayer exchange interaction only affects the top layer at the interface. The magnetization reversal of this layer along the external field occurs when the interaction energy of the external magnetic field with all layers surpasses the interaction energy of the exchange field with only the top layer.
As a result, the magnetic field of the interlayer exchange should be calculated as the measured Hex multiplied by the number of atomic layers of ferromagnetic top layer. In the references cited above, the thickness of the ferromagnetic (Fe/Pt) layer is 2 nm, equivalent to 20 atomic layers. This means that the measured magnetic field of the interlayer exchange equals 1.4 T * 20 = 28 Tesla.
(reason 2) Interlayer exchange interaction is substantially weaker than conventional exchange interaction (e.g. between Fe atoms)
The spacer layer of a very different material is inserted, which electrons have a different symmetry, size and etc. The exchange interaction is strong only between very similar electrons.
Why is the measured interlayer exchange coupling always antiferromagnetic (Figs 45,46) ? Why does its polarity not oscillate between ferromagnetic and antiferromagnetic?
The ferromagnetic contribution arising from the electron-nucleus Coulomb interaction is easily affected by the insertion of a thin layer, whereas the antiferromagnetic contribution due to the electron-electron spin-dependent Coulomb interaction remains robust.
This indicates that although the Coulomb repulsion between two electrons of two ferromagnetic layers substantially changes with variations in their mutual spin angle and, consequently, their positions, the change in electron position does not influence the position between the electron and nucleus.
The strength of the electron-electron antiferromagnetic interaction decreases as the distance between layers, and thus between the two interacting electrons, increases. This strength oscillates as an additional atomic layer is added between the two interacting electrons.
Additionally, an indirect interaction between spins promotes the antiferromagnetic exchange interaction. See below.
Why is there a hysteresis loop in measurement of Fig.47?
The energy of the magnetostatic interaction between two ferromagnetic layers differs when the magnetization of the layers is parallel and antiparallel.
The reversal of magnetization between ferromagnetic and antiferromagnetic alignments is energetically favorable to occur within a magnetic domain, confined to a limited area of an optimum finite size. This minimizes the change in magnetostatic energy. The process of domain nucleation is driven by thermal fluctuations. The domain size cannot be too large because the energy of a thermal fluctuation would be insufficient to nucleate it. Similarly, the domain size cannot be too small because the positive energy of the domain wall would counteract the negative bulk energy.
In the case of a sharp, square-shaped coercive loop, the domains are of the nucleation domain type, which are not stable and immediately expand over the entire sample after nucleation.
When a layer thicker than one atomic layer is inserted between two ferromagnetic materials, the Coulomb interaction between the electrons of different ferromagnetic layers is almost non-existent, leading to the absence of direct exchange interaction. However, in this structure, there exists an exchange interaction between the electrons of the first ferromagnetic layer and the inserted layer, between the electrons of the inserted layer itself, and between the electrons of the inserted layer and the second ferromagnetic layer. Consequently, all spins through the structure are aligned and, therefore, the magnetization of the first and second ferromagnetic layers becomes aligned as well. This phenomenon is known as the Indirect exchange interlayer interaction.
Strengthen of the exchange interaction at interface |
 |
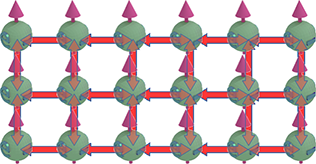| Within the bulk material, every electron engages in the exchange interaction with four nearby electrons. In contrast, at the upper and lower interfaces, an electron's exchange interaction is limited to three neighboring electrons. The strength of the exchange interaction is stronger for the interface electrons. This distinction arises from the exchange interaction's sensitivity to the number of electrons involved simultaneously ( See Fig. 61a below). As this number grows, the strength of the exchange interaction decreases precipitously. |
| click on image to enlarge it. |
(reason 1: for increase of strength of the exchange interaction): A decrease of number of electrons, with which one electron engages in the exchange intraction.
The exchange interaction is most substantial when one electron interacts with one another electron, forming a single pair. As the number of electrons interacting with one electron increases, the exchange interaction weakens.
(reason 2: for increase of strength of the exchange interaction): The dissolution of similar electron orbitals by different orbital types (due to factors like size or symmetry) in a compound.
The exchange interaction is at its strongest only between highly similar electrons and weakens between electrons of different sizes or symmetries. Additionally, the exchange interaction weakens when an electron interacts with a larger number of neighboring electrons. When an atom is situated amidst both similar and different atoms, the electron orbitals of the dissimilar atoms have minimal impact on the exchange interaction. Instead, the exchange interaction intensifies with the few remaining electrons of the same type.
Strengthen of the exchange interaction at an interface(reason : number of engaged electrons is smaller) for strengthen of the exchange interaction at an interface
The electron located at the interface engages with a smaller number of electrons in the exchange interaction compared to the electron within the bulk.
Across the interface, the electrons of a different material typically exhibit distinct sizes, radial distributions, and symmetries, making them significantly different from the electron situated at the interface. Consequently, the exchange interaction of the electron with these dissimilar electrons is minimal.
 |
||
|---|---|---|
| The exchange interaction refers to the phenomenon where the Coulomb interaction and other interactions between two particles are diminished as they combine into a single particle, restoring a previously broken symmetry, often the time-inverse symmetry. However, this merging process is restricted to fully identical particles. Discrepancies in electron size, orbital moment, spatial symmetry, or velocity between two electrons makes the merging process more difficult, resulting in a weaker exchange interaction. | The exchange interaction arises from the restoration of broken time-inverse symmetry in a pair of electrons, leading to a reduction in their Coulomb interaction. This restoration occurs specifically in a pair of electrons. However, when an electron interacts with multiple electrons, multiple pairs compete to restore this symmetry, hindering the process. Consequently, the restoration of symmetry becomes challenging for each pair, resulting in a weakened exchange interaction. (see Fig61a below) |
Proximity effect. 1st. localized electrons |
 |
| Interface between a ferromagnetic and a non-magnetic material. The green balls show the electrons of the ferromagnetic material. The blue balls show the electrons of the non-magnetic material. Even though the spins are not aligned in the bulk of the non-magnetic material, they are aligned at the interface. |
| The exchange interaction with aligned spins of the ferromagnetic material leads to the alignment of spins in the nanomagnetic material. |
| click on image to enlarge it |
The proximity effect refers to the alignment of electrons in a non-magnetic material when it is in close proximity to an interface with a ferromagnetic or antiferromagnetic material.
There are two very different types of the proximity effect:
(proximity effect 1): due to localized electrons
The effect describes the alignment of spins of non-magnetic material in proximity of its interface with a ferromagnetic or antiferromagnetic material.
(proximity effect 2): due to conduction electrons
The effect describes a diffusion of spin polarized electrons from a ferromagnetic metal to a non-magnetic metal. As a result, the conduction electrons in the non- magnetic metal become spin-polarized in close proximity to the interface.
Proximity effect. 2nd. conduction electrons |
 |
| Spin- polarized conduction electrons diffuse from the ferromagnetic metal into the non-magnetic metal. As a result, at boundary the conduction electrons in non- magnetic metal become spin- polarized |
| click on image to enlarge it |
The exchange reduces the strength of the Coulomb repulsion between two electrons, compelling their spins to align in opposite directions. This alignment results in the opposite directions of the broken time-inverse symmetry for these electrons and , therefore, the smallest degree of the broken time-inverse symmetry for the pair of the electrons .
When a third electron is present nearby, each pair of electrons experiences a force that compels their spins to align in an antiparallel manner. Time-inverse symmetry and consequently weaken the Coulomb repulsion between them.
The interplay among these three pairs of interacting electrons introduces complexity to the exchange interaction, leading to spin alignments at specific angles, distinct from both parallel and antiparallel configurations. This intricate exchange interaction, involving an odd number of electrons, is known as the Dzyaloshinskii–Moriya exchange interaction.
Only a pair of electrons with opposite spins can unbreak the broken time- inverse symmetry. When these two electrons approach each other, the broken time-inverse symmetry gradually becomes unbroken, ultimately transforming the two electrons into a single elementary particle.
| The exchange interaction arises from the restoration of broken time-inverse symmetry in a pair of electrons, leading to a reduction in their Coulomb interaction. This restoration occurs specifically in a pair of electrons. However, when an electron interacts with multiple electrons, multiple pairs compete to restore this symmetry, hindering the process. Consequently, the restoration of symmetry becomes challenging for each pair, resulting in a weakened exchange interaction. |
When 3 electrons interact and two spin-down electrons approach a spin-up electron from opposite sides, the spin-up electron can pair either with the left or the right spin-down electron in order to form a pair and to unbreak the broken time- inverse symmetry. As a result, there is a competition between two pairs: center & left electrons and center & right electrons
(fact): When an electron approaches a pair of electrons with opposite spins, it affects the strength of the exchange interaction between those electrons.
Despite the distances and spin directions remaining unchanged, the Coulomb interaction between the center and left electrons undergoes significant changes when a third electron approaches the center electron from the right side. This alteration arises due to the exchange interaction between the left and center electrons being influenced by the exchange interaction between the center and right electrons. Consequently, as the exchange interaction between the center and right electrons intensifies, the exchange interaction between the center and left electrons weakens.
Coulomb interaction between three electrons as function of their spin angles |
 |
| Coulomb repulsion between three electrons as a function of spin angle of the down electron. The density of lightning bolts indicates the strength of the Coulomb repulsion between each pair of electrons. The distance between electrons in each pair is equal. |
| click on image to enlarge it |
The exchange interaction between two electrons causes their spins to align only either in an antiparallel or parallel manner. However, when it comes to three electrons, the exchange interaction allows for a range of angles between their spin orientations. In such cases, when the exchange interaction promotes a non-collinear alignment of spins, it is referred to as the Dzyaloshinskii- Moriya exchange interaction.
| Equilibrium alignment between spins of three electrons |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||
| Exchange interaction between three electrons, when the distance between electrons in each pair is equal | ||||||||||||
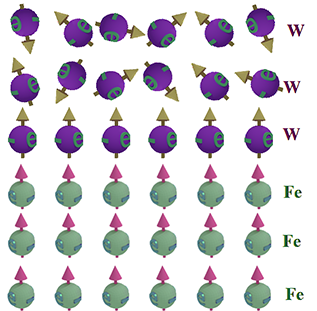
Non-collinear exchange interaction at an interface between ferromagnetic Fe and non-magnetic W |
 |
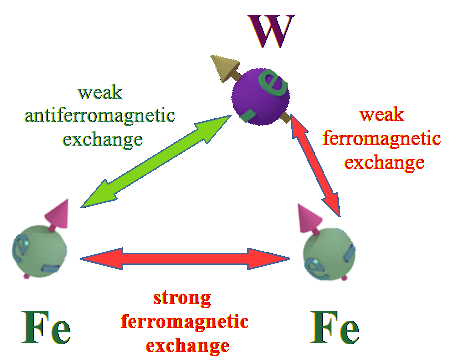| Exchange interaction at the interface between Fe (lower part) and W (upper part) The arrows show the direction of the exchange interaction. Spins of Fe are aligned ferromagnetically. However, due to the exchange interaction between spins of Fe and W, the alignment of Fe spins becomes non-collinear. This is because the left Fe spins are attempting to align antiparallel to the W spins, while the right Fe spins are trying to align parallel to the W spins, but the strong ferromagnetic exchange keeps both Fe spins parallel. As a result, the Fe spins are slightly misaligned. |
| (weak & strong exchange interaction) The exchange interaction is strong between spins of Fe and weak between spins of Fe and W, because of large differences between electron orbitals of Fe and W (sizes, symmetries etc.). The exchange interaction is only strong between very similar electrons (See above). |
| (ferromagnetic & antiferromagnetic exchange): The polarity of the exchange interaction depends on the distance between orbitals (See above). As the distances from the W orbital to the left and right Fe orbitals differ, the polarity of the exchange interaction is opposite for the two Fe- W pairs. |
| click on image to enlarge it |
This is the type of the most known and most studied Dzyaloshinskii–Moriya exchange interaction.
The presence of this effect results in a slight misalignment of spins that would otherwise be ferromagnetically aligned at the interface between a ferromagnetic and non-magnetic material.
Important properties of this type of the Dzyaloshinskii–Moriya exchange interaction:
(property 1) repulsion of domain walls
(property 2) critical for the existence of a magnetic skyrmion
(origin of the effect):
One plausible explanation for this effect is the distinct polarity of the exchange interaction between the spin of the non-magnetic material and the different spins of the ferromagnetic metal. This difference arises from the varying distances between the orbitals of the non-magnetic material and the two orbitals of the ferromagnetic metal.
This effect is weak and creates only a small misalignment of the spins because:
The exchange interaction is strong between spins of ferromagnetic metal, but is weak between and weak between spins of Fe and W, because of large differences between electron orbitals of Fe and W (sizes, symmetries etc.). The exchange interaction is only strong between very similar electrons
Essential conditions for the existence of this type of the Dzyaloshinskii–Moriya exchange interaction
(essential condition 1): At the interface, the electron of the non-magnetic metal should experience exchange interaction with multiple electrons of the ferromagnetic metal.
(essential condition 2): The spin of the non-magnetic material should experience both ferromagnetic and antiferromagnetic exchange interactions with electrons of the ferromagnetic metal, depending on its distance to the corresponding electrons.
Approximated Hamiltonian for Non-collinear Exchange interaction. Dzyaloshinskii–Moriya Hamiltonian |
 |
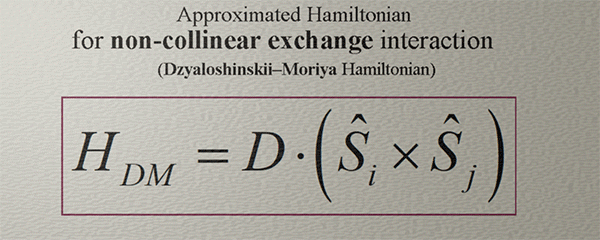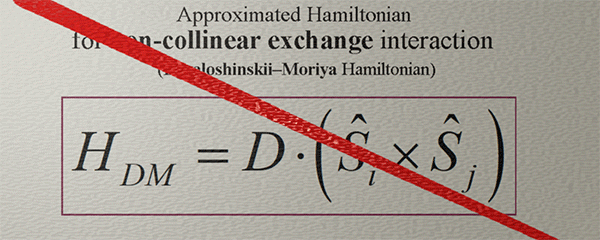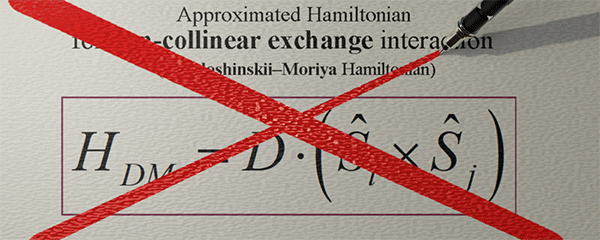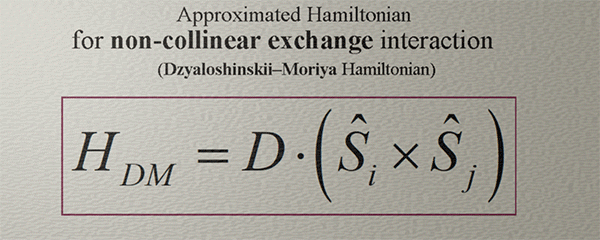| (note) This Hamiltonian captures only a very general tendency that the spins can be aligned non-collineary |
| In fact,, the non-collinear exchange interaction exhibits a remarkable complexity, richness, and intrigue. |
| (contradiction): Fundamentally, the non-collinear exchange interaction arises in a system of three or more spins, while this Hamiltonian specifically describes the interaction between only two spins. |
| click on image to enlarge it |
To characterize the Non-collinear exchange interaction, the scalar vector product in the Hamiltonian of the exchange interaction is replaced with the cross vector product.
As simple as that:
Conventional exchange interaction: Scalar vector product:
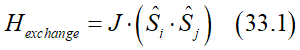
Non-collinear exchange Interaction. Cross vector product:
(fact): While the oversimplified description in Eqs.(33.1) and (33.2) may yield correct results in many cases, the exchange interaction exhibits a more diverse, intriguing, rich and complex nature.
|
| (fact): The most straightforward approach is not always the most accurate. |
The cases when the oversimplified description in Eq.(33.2) is not valid:
(contradiction 1): Contradiction in number of spins
Fundamentally, the non-collinear exchange interaction arises in a system of three or more spins, while Eq. (33.2) specifically describes the interaction between only two spins.
While the exchange interaction attributed to the spin is widely recognized and extensively studied, there exists a lesser-known variant of exchange interaction that stems from the orbital moment.
This type of exchange interaction is responsible for the high stability observed in half-filled orbitals and the ferromagnetic alignment of d-electrons in materials like Fe, Co, and Ni.
| There is nothing inherently unique or special about the spin. The spin is merely one among many properties of elementary particles that characterizes the broken time-inverse symmetry. The exchange interaction resulting from spin is a consequence of restoring or unbreaking this symmetry. |
| Similarly, the orbital moment is another property of elementary particles, representing the broken rotational symmetry. The exchange interaction due to the orbital moment arises as a result of restoring or unbreaking this rotational symmetry. |
(fact: essence of exchange interaction): The exchange interaction describes the process of combining two or more electrons into a single elementary particle. During this process, any interaction or force between the electrons ceases to exist.
(fact: exchange interaction & symmetry): The exchange interaction is not about the spin, but about symmetry. It described how one specific symmetry, which distinguishes between two electrons as separate particles, is unbroken and, as a result, two or more electrons combine into a single elementary particle.
Essence of exchange interaction. What exchange interaction does.The exchange interaction gradually reduces and eventually stops the Coulomb repulsion between certain amount of electrons.
(spin-type conventional exchange interaction) :
It switches off the Coulomb repulsion between electrons of the same orbital moment.
(2 broken symmetry parts): spins s=+1/2 & s=-1/2 are unbroken
(p- orbital- type exchange interaction) :
It switches off the Coulomb repulsion between electrons of the same spin direction .
(3 broken symmetry parts): p- orbital moment l=+1/2 & l=-1/2 & l=0 are unbroken
(d- orbital- type exchange interaction) :
It switches off the Coulomb repulsion between 
electrons of the same spin direction .
(5 broken symmetry parts): d- orbital moment l=+3/2 & l=-3/2 &l=+1/2 & l=-1/2 & l=0 are unbroken
electrons vs p- orbital: electrons or d- orbital: electrons or f- orbital:
electronsThe exchange interaction due to spin can be induced with just two electrons. This is because the time-inverse symmetry described by spin has only two broken parts, corresponding to the forward and backward flow of time.
The exchange interaction due to p- orbital moment can be induced only by three electrons. This is because the p- rotational symmetry has 3 broken parts.
The exchange interaction due to d- orbital moment can be induced only by five electrons. This is because the d- rotational symmetry has 5 broken parts.
The exchange interaction due to f- orbital moment can be induced only by seven electrons. This is because the f- rotational symmetry has 7 broken parts.
stable quantum states of unbroken symmetry |
|||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| When either the broken time- inverse symmetry or the broken rotational symmetry is unbroken, the quantum state becomes very stable possessing a low energy. | |||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Zayets 2023.08 |
(Why Cr & Mn are not ferromagnet) Why are Mn (3d5 4s2) and Cr (3d5 4s1) not ferromagnetic despite having 5 unpaired d-electrons with perfectly aligned spins, whereas Fe (3d6 4s2), Co (3d7 4s2), and Ni (3d8 4s2) are ferromagnetic despite having 4, 3, and 2 unpaired d-electrons, respectively?It is because the total spin of five d- electrons in Mn and Cr is only 1/2. The d- orbital of Mn and Cr is half-filled. It means the d- rotational symmetry is fully unbroken. As a result, all five electrons combine into one electron with spin 1/2.
(Why V & Ti are not ferromagnet) Both Co (3d7 4s2) and V(3d3 4s2) have 3 unpaired d- electrons. Both Ni (3d8 4s2) and Ti(3d2 4s2) have 2 unpaired d- electrons. Why are Co and Ni are ferromagnetic, but V and Ti are not?The distinct magnetic behavior between Co (3d7 4s2) and Ni (3d8 4s2) compared to V (3d3 4s2) and Ti (3d2 4s2) is due to the properties of the orbital exchange interaction. The d-orbital filling in Co and Ni is beyond half-filled, whereas in V and Ti it remains below half-filled. The orbital exchange interaction is strongest when half of the orbital is already filled. In this case the orbital exchange interaction strongly aligns spins in one direction. Addition of an electron slightly weakens the strength of the spin alignment, but it still remains strong. In contrast, removal of an electron from the perfect half- orbital filling disturbs the orbital exchange interaction substantially.
(result of adding an electron to a half- occupied state): some orbitals unavoidably become double- occupied and different from other single- occupied orbitals. The orbital exchange is strongest only between identical electrons.
(Why Co is strongest ferromagnet, Fe is weaker and Ni is weakest) Why is it that Fe, with 4 unpaired d-electrons, exhibits weaker ferromagnetism compared to Co, which has only 3 unpaired d-electrons? Conversely, why does Ni, with 2 unpaired d-electrons, demonstrate weaker ferromagnetism compared to both Co and Fe?The observed behavior can be attributed to the specific characteristics of the exchange interaction attributed to the orbital moment. This type of exchange interaction has a significant impact on aligning the spins of d-electrons in Fe, Co, and Ni in a parallel fashion. However, it also has another distinct feature that results in a reduction of the overall spin of the system.
In the ideal scenario involving five d-electrons, where this exchange interaction is at its strongest, the total spin is notably lowered to 1/2 (case of Mn or Cr). The iron, with one additional d-electron beyond this optimal setup, experiences a reduction in its total spin, although not as much as in the case of five electrons. On the other hand, Co possesses two extra d-electrons in comparison to the ideal case, but due to being further away from the optimum, the reduction in the total spin of its d-electrons is relatively weaker, leading to a larger overall spin. This difference is why Co exhibits stronger ferromagnetic properties when compared to Fe.
In contrast, Ni only has 2 unpaired d-electrons, which is a small number, resulting in a low total spin for its d-electrons. Consequently, Ni displays weak ferromagnetic behavior.
(Why Cu is not a ferromagnet) The copper has one additional electron in comparison to Ni, so then why is the copper not ferromagnetic?The d- orbital of Cu (3d10 4 s1) is fully filled and, therefore, Cu does not have unpaired d- electrons.
(orbital- type exchange & spin alignment) Why does the orbital- type exchange interaction align spins?The exchange interaction driven by the orbital properties exclusively takes place among electrons that share exceptional similarity. It means that all parameters of interaction electrons should be very the same. It includes the spin. The spins of all these electrons must be oriented in the same direction. Only in this case there is no Coulomb repulsion between all interacting electrons and the electron energy is lowest.
In the event that even a single electron's spin is misaligned, the requisite condition for the orbital-type exchange interaction is disrupted, leading to the reinstatement of the Coulomb repulsion between electrons among the electrons, subsequently elevating the total energy of the electron system. Therefore, the misalignment in spin orientation is energetically unfavorable due to the increase in total energy and the orbital- type exchange interaction forces all spins to align in the same direction.
Do you possess any experimental evidence substantiating the existence of the orbital-type exchange interaction??
Proves for existing the orbital-type exchange interaction:
(prove 1): Ultra- high stability of the half- filled orbitals.
The conventional spin-type exchange interaction is unable to explain the experimentally observed and well-verified ultra-high stability of half-filled orbitals. In contrast, the presence of the orbital-type exchange interaction offers a straightforward explanation for this phenomenon.
(prove 2): Absence of ferromagnetism in a material with a half- filled orbital (Mn, Cr etc)
The d- orbital of Mn and Cr is exactly half- filled. The spins of their five electrons are perfectly aligned. Even though these materials have the largest possible number of the aligned d- electrons, they are not ferromagnetic. In contrast, materials with over half-filled orbitals and a smaller count of aligned d-electrons, such as Fe, Co, and Ni, display ferromagnetic properties.
These phenomena can be explained only due to the existence of the orbital- type exchange interaction.
(prove 3): Preferential Filling of Singly-Occupied Orbitals over Doubly-Occupied Orbitals (1st Hund's Rule)
The 1st Hund's rule is perfectly explained by the orbital exchange interaction. Neither the conventional spin exchange interaction nor the spin- orbit cannot explain the experimentally- observed 1st Hund rule. Even more, both the spin exchange interaction nor the spin- orbit act against the 1st Hund rule.
(prove 4): Alignment of all spins of all singly- occupied orbital in one direction (2nd Hund's Rule)
The 2nd Hund's rule is perfectly explained by the orbital exchange interaction. Neither the conventional spin exchange interaction nor the spin- orbit cannot explain the experimentally- observed 2nd Hund rule. Even more, both the spin exchange interaction nor the spin- orbit act against the 2nd Hund rule. The spin exchange interaction forces spins to align opposite to each other. While the spin- orbital interaction forces the spins in different directions along specific orbital moments.
(prove 5): Absence of ferromagnetism in a material, whose orbital is filled less than a half. (Ti, V etc)
Even though the spins of electrons are aligned in parallel in an orbital filled below half-fill (the 2nd Hund rule), there is no ferromagnetic alignment between neighboring atoms (e.g., Ti, V). The parallel spin alignment within one orbital is due to the orbital exchange interaction.
Orbital energy is at its lowest when it is half-filled or completely filled. Therefore, an orbital filled below half-fill becomes more stable when it accepts an additional electron rather than sharing one of its own for interatomic bonding. In contrast, an element with an orbital that is more than half-filled (e.g., Fe, Co) readily shares its electrons for bonding. The lower electron count for this element brings the orbital closer to half-fill, resulting in lower energy. The spin of the bonding electron can only align opposite to the spins of the remaining half-filled electrons for each of the two neighboring atoms. This causes the spins of the half-filled orbitals of neighboring atoms to align in the same direction (ferromagnetic alignment).
The sequence of orbital filling is determined by the Aufbau principle and Hund's rule, influenced by the interplay of spin-type exchange interaction, orbital-type exchange interaction, and spin-orbit interaction. The remarkable stability of half-filled and fully-filled orbitals significantly impacts the prioritization of filling order.
There are 3 mechanisms, which influence the order of orbital filling: (1) orbital exchange interaction (strongest); (2) spin- exchange interaction (moderate); (3) spin- orbit interaction (weakest).
The
The spin-orbit interaction is just the magnetic field of a relativistic origin, which is forcing the electron spin to align along its own direction.
(origin of spin- orbit interaction) : The magnetic field of spin- orbit interaction is created by an electrical field of the nucleus due to orbiting the electron around the nucleus. When an electron moves in electrical field, it experience a magnetic field. It is a relativistic feature of the electromagnetic field. The similar relativistic effect is Lorentz force: .When an electron moves in a magnetic field, it experience an electrical field, which forces the electron to turn from a straight movement.
(fine structure): a tiny difference in electron energy due to spin-orbit interaction
The fine structure describes a tiny difference in electron energy for the opposite directions of spin with respect to the direction of the magnetic field of spin- orbit interaction.
Spin- Orbit Interaction acts against experimentally- observed Hund's rules
(alignment of spin in different directions by SO):
Direction of the magnetic field of spin- orbit interaction Hso is different for each orbital state. E.g. Hso is opposite for l=+1/2 and l=-1/2. Hso forces the spin to align along itself and, therefore, in a different direction for each orbital, which contradicts the 2nd Hund's rule
Aufbau principle |
||||
|
||||
| the pictures are copied from here |
The Aufbau principle dictates that electrons fill atomic orbitals in increasing order of energy levels. Following this principle, electrons occupy the available atomic orbitals with the lowest energy levels before those with higher energy levels.
At first the 1s orbital is fully filled, next 2s orbital is fully filled, next 2p orbital is fully filled, next 3s orbital is fully filled, next 3p orbital is fully filled, next 4s orbital is fully filled, next 3d orbital is fully filled and so on.
Breaking of the Aufbau principleWhen an orbital shell is close to being half-filled or full-filled, one electron from a lower-energy shell is moved to the next orbital shell in order to achieve a half-filled or full-filled state for the orbital.
(reason) The half-filled or full-filled orbitals possess very low energies, making it energetically favorable to create such configurations even if it involves transferring an electron from a lower-energy shell.
(Examples):
(half- filled shell) :
Cr: [Ar] 3d5 4s1; Mo: [Kr] 4d5 5s1;
(full- filled shell) :
Cu: [Ar] 3d10 4s1; Ag: [Kr 4d10 5s1;
1st Hund's rule |
 |
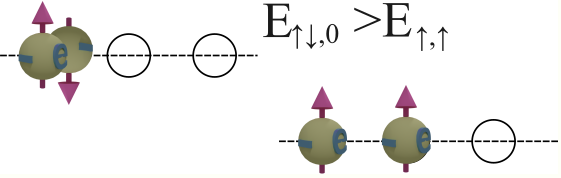Fig.67 1st Hund's rule states that the state in which one orbital is singly occupied by one electron (as shown on the right) has lower energy compared to the state where the orbital is doubly occupied by two electrons with opposite spins (as shown on the left). As a result, the state with singly occupied orbitals becomes the equilibrium state. |
| (one orbital is occupied by two electrons with opposite spins (shown at the left)): There is no Coulomb repulsion between two electrons. Therefore, the positive repulsion energy is zero. There is no spin- orbit interaction, the double occupied state does not have spin. As a result, the negative energy of spin- orbit interaction is zero. |
| (state occupied by two electrons with opposite spins (shown at the right)): There is a Coulomb repulsion between two electrons, resulting in a positive Coulomb repulsion energy that contributes to the total energy. Additionally, each electron possesses spin and experiences the spin-orbit interaction, which contributes negatively to the total energy. |
(state of Hund's rule): For the orbital filling shown on the right, the gain in negative energy from the spin-orbit interaction outweighs the negative Coulomb repulsion. As a result, the total energy decreases, making the orbital filling, which is shown on the right, the equilibrium state. |
The Hund's rules are empirical rules, which defines the order of the orbital filling and the spin alignment for the electrons filling the same atomic orbit.
The Hund's Rules are comprehensively determined by the Orbital Exchange Interaction and faithfully encompass all attributes associated with the Orbital Exchange Interaction
(1st Hund's rule): The 1st Hund's rule states that at first all orbital is singly occupied before any orbital becomes doubly occupied by two electrons of opposite spins.
(2nd Hund's rule): The 2nd Hund's rule states that spins of all singly- occupied orbital are aligned in one direction
(fact 1): Hund's Rules are determined by Orbital Exchange Interaction and embody all attributes of Orbital Exchange Interaction
(fact 2): Both the Spin- Exchange Interaction and the Spin- Orbit Interaction act against Hund's rules
( orbital exchange interaction): 
(force direction): it forces singly- occupation of a state before double- occupation (supports 1st Hund's rule)
The orbital exchange interaction compels the full occupation of at least one orbital state. For instance, in the case of p-rotation symmetry, it enforces the single occupation of states l=-1, l=0, and l=+1 in order to completely restore the broken p-rotation symmetry.
( spin exchange interaction): (force direction): it forces double - occupation of a state before single- occupation (acts against 1st Hund's rule)
The spin exchange interaction compels occupation of each state by two electrons of opposite spins in order to completely restore the broken time- inverse symmetry.
( spin- orbit interaction): (force direction): it forces singly- occupation of a state before double- occupation (supports 1st Hund's rule)
The spin-orbit interaction describes a magnetic field along which the electron spin aligns itself if no other forces act upon it. This interaction results in negative energy, making it energetically favorable for the electron to experience the spin-orbit interaction. Conversely, a double-occupied state lacks spin and, therefore, does not engage with the spin-orbit interaction. Consequently, the spin-orbit interaction promotes the single occupation of a state over double occupation from an energy perspective.
Hund's rules |
||||||||||||
Hund's Rules are determined by Orbital Exchange Interaction and embody all attributes of Orbital Exchange Interaction |
||||||||||||
|
||||||||||||
| (fact): Both the Spin- Exchange Interaction and the Spin- Orbit Interaction act against Hund's rules | ||||||||||||
| The Orbital Exchange Interaction dominates over the Spin-Exchange Interaction and the Spin-Orbit Interaction to ensure the fulfillment of Hund's rules |
( orbital exchange interaction): (force direction): It forces the parallel spin alignment.(supports 2nd Hund's rule)
The orbital exchange interaction reaches its maximum strength when identical electrons occupy all states with broken rotational symmetry. It means that it is most potent when all electrons have parallel spins. Consequently, the orbital exchange interaction enforces parallel spin alignment.
( spin exchange interaction): (force direction): It forces the opposite spin alignment. (acts against 2nd Hund's rule)
The spin exchange interaction compels occupation of each state by two electrons of opposite spins in order to completely restore the broken time- inverse symmetry. Consequently, the spin exchange interaction enforces opposite spin alignment.
( spin- orbit interaction): (force direction): It forces the spin alignment in different directions. (acts against 2nd Hund's rule)
The spin-orbit interaction describes a magnetic field Hso, whose direction aligns with the spatial asymmetry of the electron wavefunction. As a result, the direction of this magnetic field varies for each orbital state. For instance, states with l=-1 and l=+1 experience opposite Hso. Consequently, the spin-orbit interaction enforces spin alignment in different directions for each orbital state.
(note) : For a long time, the explanation of Hund's rules in physics was somewhat perplexing and not entirely comprehensible. This confusion stemmed from the robust spin exchange interaction, which significantly contradicted the Hund's rules. However, it was only after my discovery of the even more potent orbital exchange interaction in July 2023 that all the puzzles surrounding Hund's rules were finally resolved. It allowed for a clear and comprehensive understanding of the physics behind the Hund's rules, as all the properties of the orbital exchange interaction aligned seamlessly with these rules.
(a bad scientist) : For quite some time, Hund's rules remained a source of confusion, and their origin was shrouded in uncertainty. Many scientists, myself included (see my old comments in the comment session below) , initially speculated that the spin-orbit interaction might be responsible for Hund's rules. However, this belief persisted despite the fact that the spin-orbit interaction is relatively weak and thus cannot serve as the primary driving force behind the rules governing orbital filling and despite the fact that Hund's rules did not align well with the properties of the spin-orbit interaction.
The full- filled states are orbital states in which all states of rotation symmetry and time- inverse symmetry are filled by electrons. An element that possesses no additional electrons apart from those filling full- filled states is called inert gas.
Full- filled orbital |
||||||||||||||||||
|
||||||||||||||||||
| Whole full- filled orbital interacts with other electrons or with small/moderate external field as one single elementary particle |
( merging into one elementary particle): Even though the full-filled state is filled by several electrons, all electrons literally merge into one elementary particle. The full-filled state interacts with external forces, nucleus and other electrons as one single particle.
( spatial distribution): The distribution of a full-filled state is a perfect sphere.
It is because the orbital moment of the full- filled state is zero and the rotation symmetry is not broken for this state.
( high stability of full- filled state): It requires a high energy to excite an electron from a full-filled state.
Because the full- filled state is truly a single elementary particle, there is no Coulomb repulsion between the electrons filling this state. However, when one electron is excited out from the full- filled state, Coulomb repulsion between electrons is restored, adding a significant positive Coulomb repulsion energy to the energy of the excited level (refer to Fig. 71 below). This explains the high stability of the full- filled state.
& 
( spin & orbital moment): The full- filled state does not spin and orbital moment.
It is because the rotation symmetry and time-inverse symmetry are unbroken for this state
Elements with a full- filled orbital:
neon Ne: [Ar] 2s² 2p6; argon Ar: [Ne] 3s² 3p6;
zinc Zn: [Ar] 4s² 3d10; cupper Cu: [Ar] 4s¹ 3d10;
| Full-filled shells | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| The spatial distribution (wavefunction) of a full- shell is of ideally spherical shape. It has no spin and no orbital angular momentum. It is always a single elementary particle independently of how many electrons it combines. | ||||||||||||||||||||
|
||||||||||||||||||||
| click on image to enlarge it |
Why is Zinc not an inert gas? It has all its orbitals full- filled as in the case of an inert gas.It is because in the case of an inert gas the most external shell is of the p- type, but in zinc the most external shell is of the s- type. The full- filled p-type shell is more difficult to break than full- filled s-type shell. A breaking out of one electron from a full- filled p- shell restores the Coulomb repulsion between 5 electrons adding a substantial positive energy to the shell. As a consequence, it requires a larger energy to remove one electron from the inert gas shell. In contrast, a breaking out one electron from a full- filled s- shell does not restore any Coulomb repulsion.
The half- filled states are orbital states in which all states of rotation symmetry are filled by electrons. In this case, the orbital is filled with half the number of electrons compared to the orbital of an inert gas.
Half- filled orbital |
||||||||||||||||||
|
||||||||||||||||||
| Whole half- filled orbital interacts with other electrons or with small/moderate external field as one single elementary particle |
( merging into one elementary particle): Even though the half -filled state is filled by several electrons, all electrons literally merge into one elementary particle. The half-filled state interacts with external forces, nucleus and other electrons as one single particle.
( spatial distribution): The distribution of a half -filled state is a perfect sphere.
It is because the orbital moment of the half- filled state is zero and the rotation symmetry is not broken for this state.
( high stability of half- filled state): It requires a high energy to excite an electron from a half -filled state.
Because the half- filled state is truly a single elementary particle, there is no Coulomb repulsion between the electrons filling this state. However, when one electron is excited out from the half- filled state, Coulomb repulsion between electrons is restored, adding a significant positive Coulomb repulsion energy to the energy of the excited level (refer to Fig. 71 below). This explains the high stability of the half- filled state.
& ( spin & orbital moment): The half- filled state has the spin equal to 1/2 (the same as the spin of a free electron) , but does not have orbital moment.
It is because the rotation symmetry are unbroken, the time-inverse symmetry is still broken for this state. Since the half - filled is one single elementary particle, its broken time inverse symmetry is described by the spin equal to 1/2.
Elements with a half- filled orbital:
nitrogen N: [He] 2s² 2p³;
phosphorus P: [Ne] 3s² 3p³ ; arsenic As: [Ar] 3d10 3s² 3p³
cromium Cr: [Ar] 3d5 4s¹; manganese Mn: [Ar] 3d5 4s²;
| Half-filled shells | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| The spatial distribution (wavefunction) of a half- shell is of ideally spherical shape. Its spin equals 1/2. It has no orbital angular momentum. It is always a single elementary particle independently of how many electrons it combines. | |||||||||
|
|||||||||
| Full-filled orbitals do not have spin. Only a half- filled state has spin, which is shown by green ball with arrow and equals 1/2 | |||||||||
| click on image to enlarge it |
Why is the spin of the half-filled d-orbital of Mn only 1/2, even though it is filled by 5 electrons with spins, all of which are parallel, and each spin equals 1/2? = 
This is because the half-filled orbital effectively becomes a single elementary particle. Spin describes the breaking of time- inverse symmetry, and time- inverse symmetry can only be broken once for a single elementary particle. This is why the spin of the half-filled d-orbital of Mn is 1/2, rather than 5 times 1/2.
Whole half- filled orbital or full-filled orbital interacts with other electrons or with small/moderate field as one single elementary particle
| Interaction of half- filled & full - filled orbitals with an electrical field |
|---|
 |
| Interaction of electron shells of Mn with electrical field E (blue arrow). All s- and p- orbitals are full- filled (shown in green and red). d- orbital is half- filled (shown in yellow). Each orbital interacts with the electrical field as a single particle. Each orbital elongates and shifts along the direction of the electrical charge. Since the charge and screening for each elementary particle is different, the interaction strength is different for each orbital. |
| click on image to enlarge it |
Example: Difference in orbital energy between oxygen and nitrogen Fig.70. p- orbitals of nitrogen and oxygen. A large energy difference. |
 |
| Energy of electron orbitals of Nitrogen [He] 2s² 2p³ and Oxygen [He] 2s² 2p⁴. Because the p- orbital of nitrogen is half- filled, its energy is substantially lower. Electrons within nitrogen do not experience Coulomb repulsion, whereas electrons within oxygen are subject to Coulomb repulsion (shown by light balts). It is the reason for the difference between orbital energies. |
| click on image to enlarge it |
While nitrogen and oxygen are adjacent elements in the periodic table, their ionization energies significantly differ. This discrepancy arises from the fact that the nitrogen orbital is half-filled, leading to the absence of Coulomb repulsion between its three electrons. Conversely, oxygen's orbital is occupied by four electrons. Due to the broken p-rotation symmetry, Coulomb repulsion between the electrons occurs, resulting in an increase in orbital energy for oxygen.
(Nitrogen): p-orbital is half- filled, which means it is filled by 3 identical electrons of the same spin direction. Since identical electrons filled all states of the broken p- rotation symmetry. the symmetry becomes unbroken. As a result, 3 electrons behave as one elementary particle. There is no repulsion between electrons. The charge of the particle is -3e and spin is 1/2. The shape of this joint particle is perfectly spherical without any orbital moment.
(Oxygen): One state of the p- orbital is filled by two electrons of opposite spins, other two states are filled by one electron. Since the filling of the states is not identical, the p- rotation symmetry remains unbroken and there is a Coulomb repulsion between electrons. Only there is no Coulomb repulsion between two electrons of opposite spins filling the state (l=0). As a result, there is Coulomb repulsion between 5 pairs of electrons from possible 6 pairs. The positive Coulomb- repulsion energy makes orbital energy of oxygen substantially higher.
(fact) There is no Coulomb repulsion between one pair of electrons with opposite spins in oxygen. However, the Coulomb repulsion still exists for 3 of 4 possible pairs of electrons in oxygen.
Why energy of p-orbital of nitrogen is substantially deeper than that of oxygen?
(from Govind) Why does nitrogen have a higher ionization energy than oxygen?
answer is below
The energy levels of orbitals occupied by multiple electrons in an atom are not static but dynamic, undergoing significant changes when one of the electrons is excited to another level or undergoes scattering in or out. This dynamic behavior arises from the modulation of Coulomb repulsion between electrons, resulting from changes in the orbital symmetry as the number of occupied electrons changes.
| Fig.71. Changing of energy of half-filled orbital when an electron is scattered in and out |
|---|
 |
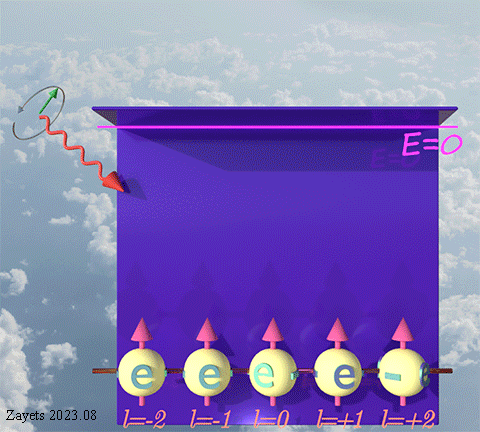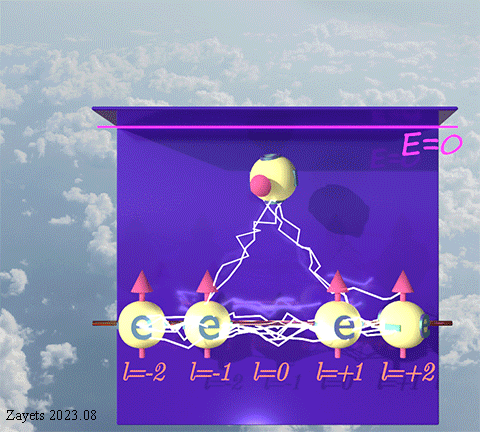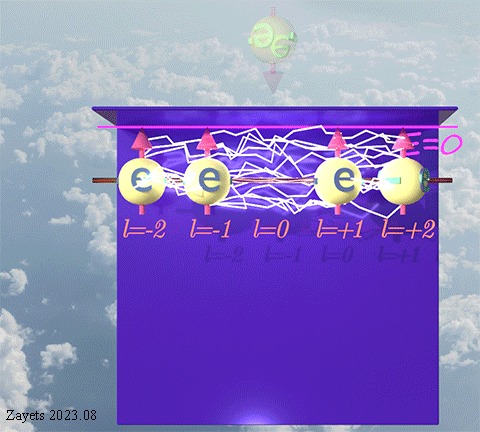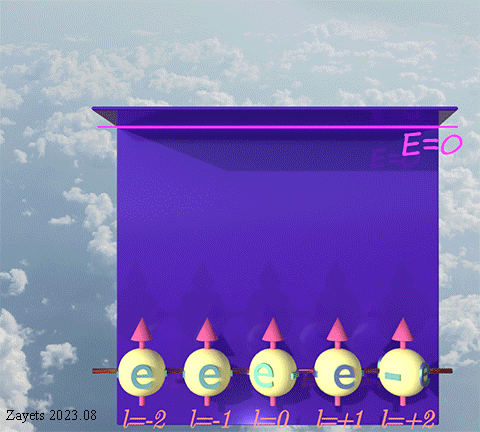| (low energy state) When the d-orbital is filled by 5 electrons (a half- filled state), there is no Coulomb repulsion between the electrons, because the d- rotation symmetry is fully unbroken. However, when a photon excites one electron out of this level, it breaks the d-rotation symmetry, leading to the restoration of Coulomb repulsion between electrons. Consequently, tthe energy of the orbital energy increases. |
| (high energy state) When the d-orbital is filled by 4 electrons, there is Coulomb repulsion between the electrons (shown by light balts) adding the positive repulsion energy to the orbital energy. When the 5th electrons is scattered into the orbital, the Coulomb repulsion is ceased and the orbital energy decreases. |
| click on image to enlarge it |
When an additional electron occupies an empty orbital state, the orbital energy can either increase or decrease. This change occurs because the addition or removal of an electron alters the positive Coulomb repulsion energy between electrons within the orbital level.
-> Energy 
The addition of an electron to an orbital level results in Coulomb repulsion between it and each electron already occupying the same orbital level. This interaction adds a positive energy to the orbital level.
-> Energy 
The addition of an electron to an orbital level may lead to the restoration of orbital rotation symmetry, consequently reducing or even eliminating Coulomb repulsion between all electrons occupying the orbital level. This, in turn, results in a decrease in the orbital energy.
Challenging problem of deep- level spectroscopy(fact) This effect makes it difficult to measure the energy of deep electron levels, because the energy level changes substantially during a probing measurement. It creates many challenging problems for deep- level spectroscopy.
It is because the Coulomb repulsion between electrons of these states is fully absent and it is switched on after an electron is scattered in or out.
Is the changing of the orbital level during its probing related to the quantum-mechanical principle that any measurement of an object's property alters that property?
No, it is related to a change of the orbital symmetry. The orbital level can be probed without changing the number of electrons occupying the specific level. Then,there is no change of the orbital energy.
(fact): The half- filled and full- filled state experience the largest change of energy when an electron scattered out or in.
vs 
(fact) Excitation of an electron from orbital level, the change of the orbital energy is larger for a full- filled state than for a half- filled state.
(reason): A full- filled state has twice as many electrons than a half- filled. Therefore, excitation of an electron from a full- filled state switches on the Coulomb interaction between a larger number of electrons
vs vs (fact) Excitation of an electron from an orbital level with higher symmetry leads to a more significant change in orbital energy. For instance,the change of energy is larger for d- orbital than for p- orbital.
(reason): The p- half-filled orbital has 3 electrons, but d-half-filled orbital has 5 electrons. Excitation of an electron from a p- half-filled level switches on the Coulomb repulsion only between 1 pair of 2 remaining electrons. In contrast, excitation of an electron from a d- half-filled level switches on the Coulomb repulsion only between 6 pairs of 4 remaining electrons.
The exchange interaction arises from a fundamental principle of nature: higher symmetry states possess lower energy, while less symmetrical states have higher energy. Consequently, the forces in nature drive quantum systems toward greater symmetry and, eventually, towards the most symmetrical state - the vacuum state or "nothingness." This force is the force of the exchange interaction
|
The higher symmetry state corresponds to a lower entropy of a quantum system. As a result, the force of the exchange interaction is lowering the entropy of the quantum system. |
(example 1): An electron and positron are forced towards each other to combine into symmetrical vacuum state.
(symmetry before): several symmetries broken representing the electron and positron; (symmetry after): none of symmetries is broken for the vacuum state;
(energy before): both energies of the electron and positron are positive. The total energy is positive; (energy after): the energy of the vacuum state is zero
(example 2): Two electrons of opposite spins are scattered to occupy one quantum state
(symmetry before): time- inverse symmetry is broken for each electron; (symmetry after): time- inverse symmetry is not broken;
(energy before): the energy is higher because of positive Coulomb repulsion energy between electrons (energy after): the energy is smaller due to absence of Coulomb repulsion energy between electrons
(example 3): Three electrons electrons of p- orbital moments l=+1/2; l=0; l=-1/2 are scattered to occupy a half- orbital state
(symmetry before): p- rotation symmetry is broken for each electron; (symmetry after): p- rotation symmetry is not broken;
(energy before): the energy is higher because of positive Coulomb repulsion energy between each of three electrons (energy after): the energy is smaller due to absence of Coulomb repulsion energy between three electrons. Because of the low energy of the half- filled orbital state, this state is ultra stable (e.g. nitrogen)
The direction of any force is determined by the direction for which the total energy of the system becomes smaller.
As a result, any quantum system is forced to a more symmetrical state. This force is the force of the exchange interaction !!!!
Inverse Trend of Entropy Change Induced by the Force of Exchange InteractionThe force of the exchange interaction drives a quantum system to transition towards a state of higher symmetry, which in turn corresponds to lower entropy within the quantum system. Consequently, the force exerted by the exchange interaction leads to a reduction in the system's entropy.
Increase of entropy for a classical system:In the classical system of the interacting particles the disorder is always increasing. As a result, the entropy is always increasing in a classical system.
Decrease of entropy for a quantum system forced by the exchange interaction:The exchange interaction forces the broken symmetries of a quantum object to be unbroken and, therefore, towards more symmetrical state. As a result, the entropy is decreasing.
Increase of entropy for a quantum system forced by the symetry breaking:The forced or spontaneous symmetry breaking makes the quantum symmetry less symmetrical and, therefore, increases the entropy of the quantum system.
(example 1-3): (1) annihilation of positron and electron (2) filling a state by two electrons of opposite spin (3) filling half- orbital state.
In all three examples, which are explained above, the entropy decreases.
(example 4): remagnetization of a ferromagnetic material when temperature decreases below the Curie temperature.
As spins are aligned in one direction, the symmetry of the quantum system increases. As a result, the entropy decreases.
(example 5): Scattering electrons in and out from deep atomic shells
The electrons of the deep atomic shells have neither the spin or orbital moment. Their distribution is perfectly spherical. When an electron scattered out from the deep atomic shell, other electrons, which fill the shell, regain the orbital moment and the spin, their distribution becomes non- spherical. It courses a substantial rise of the entropy.
For the opposite process , when the electron is scattered into an empty state of a deep atomic shell, all electrons of the deep atomic shell become very symmetric and, as a result, the entropy decreases.
In a ferromagnetic material the spins of all localized electrons are aligned in one direction.
There are 3 known single-element materials, which are ferromagnetic at room temperature:
(mateial 1): Fe iron (modest ferromagnetism)
(mateial 2): Co cobalt (strongest ferromagnetism)
(mateial 3): Ni nickel (weakest ferromagnetism)
Origin of ferromagnetism:
(spin alignment within one atom): Forced by orbital exchange interaction
The orbital exchange interaction compels a set of five identical d-electrons with parallel spins to break the rotational symmetry, resulting in the creation of a symmetric half-filled orbital (as mentioned earlier). In cases where there are six d-electrons (as in Fe), seven d-electrons (as in Co), or eight d-electrons (as in Ni), the rotational symmetry is not yet entirely broken. Nonetheless, the orbital exchange interaction still coerces the electrons towards a state that aligns their spins more closely to the symmetry-unbroken configuration.
(spin alignment between atoms): Forced by spin exchange interaction betwen elctrons of different atoms and a modulation of Coulomb atraction force between an electron and a nucleus.
Spin-dependent Coulomb repulsion between electrons in neighboring atoms causes electrons to move closer to the atomic nucleus, resulting in an increase in the negative attractive energy between the nucleus and the electron . When electron spins of neighboring electrons are parallel, the repulsion between them is stronger, leading to a stronger pushing effect and a greater increase in attractive energy. Consequently, the parallel alignment of electron spins is energetically favored.
Does the orbital exchange interaction not only promote ferromagnetic alignment among all d-electrons within the same atom but also induce ferromagnetic alignment among electrons in neighboring atoms?
As of Aug.2023, I do not know. Maybe.
Slater-Pauling curve |
|
| Average magnetic moment per an atom in a unit of Bohr magneton μ B as a function of average atomic number of a ferromagnetic compound. Note, μ B is the magnetic moment of one electron with the spin. |
| Since both magnetic moments of the spin- polarized conduction electrons and localized d-electrons contribute to the shown average magnetic moment, the moment of the localized d- electrons is smaller than shown in Fig. |
|
| click on image to enlarge it |
Iron possesses 4 unpaired d-electrons, which might lead one to expect a magnetic moment per atom of 4 μB. However, the actual magnetic moment per atom for iron is observed to be ~2.2 μB. What accounts for this difference?When considering elements like Mn or Cr, which possess one fewer d-electron, their d-orbital becomes half-filled. This configuration results in a spin of 1/2 and subsequently a magnetic moment per atom of only 1 μB. On the other hand, with an additional d-electron in the case of iron, the symmetry of the d-orbital is somewhat disrupted, leading to a larger magnetic moment. However, this moment remains in proximity to the 1 μB value characteristic of the half-filled d-orbital scenario.
Why does iron have a higher magnetic moment compared to cobalt, even though cobalt exhibits stronger ferromagnetic properties?Perhaps it's because iron is quite close to the ideally symmetrical case of a half-filled orbital, whereas cobalt is already too distant from the symmetrical case of a half-filled orbital. This is why CoFe is the most robust ferromagnetic material.
Indeed, both Fe and Co possess magnetic moments that are relatively similar, and their ferromagnetic characteristics closely align. Nevertheless, it's essential to recognize that factors beyond just magnetic moments significantly impact the strength of ferromagnetism. These additional parameters encompass lattice parameters, crystal symmetry, and the spin polarization of conduction electrons.
(fact:) Parallel spin alignment within d-orbitals and parallel spin alignment between atomic orbitals in ferromagnetic materials (e.g., Fe, Co) are distinct phenomena with fundamentally different implications.
(Parallel spin alignment within d-orbitals): Phenomenon occurs due to the orbital type exchange interaction.
(spin alignment between atomic orbitals in a ferromagnetic material): Phenomenon occurs due to the modulation of the Coulomb attraction strength between an electron and a nucleus, resulting from the spin-dependent variation in the electron-nucleus distance.
Spin Waves |
|||
|
|||
| Spin waves are waves of magnetization direction of localized electrons. They may propagate a long with only a weak absorption. The red arrows show spins of localized d-electrons. Click on image to enlarge it |
Questions & Answersabout spin dependence of the strength of the Coulomb repulsion
() Q. Now I have a special interest on coulomb repulsion energy between two electrons as function between them in your contents. Do you have a paper on this subject? If you have it, please let me know about your publication information.
The dependence of the strength of the Coulomb repulsion between two electrons on their mutual spin directions is the origin of the exchange interaction. More specifically, the dependence of the Coulomb repulsion on the degree of the breaking of the time-inverse symmetry in the system of two electrons. When electrons have opposite spins and distance between them is reduced, the degree of the broken time inverse symmetry for two electrons decreases. As a result, the strength of the coulomb repulsion decreases as well. When two electrons occupy one quantum state, the time-inverse symmetry is not broken and there is no Coulomb repulsion between two electrons. The Coulomb repulsion becomes zero.
The reason for that is that two electrons become one particle with charge -2e and no spin, when two electrons occupy one quantum state. There is nothing that could distinguish two separate particles of one quantum state in this case. There is no single property, which could be associated and make a difference between two different particles (electrons) of one state. Two electrons, which occupy one quantum state, have zero total spin and are described by a scalar wave function (not a spinor). In case if such two electrons were two particles with a zero total spin, it would be possible to distinguish whether their spin directions are up and down or left and right or front and back. However, it could not be distinguished. When two electrons occupy one quantum state, the time inverse symmetry is not broken. Therefore, there is no spin inside. It is neither up and down nor left and right nor front and back. It is one particle with zero spin, for which the time-inverse symmetry is not broken.
It means that from Quantum mechanical point of view , the one quantum state, which is occupied by two electrons, is one elementary particle without parts, but it is not a set of two interacting elementary particles. As any features (electron spin or electron special position), which could distinguish between two electrons, are fully dissolved after two electrons occupies one state, two elementary particles becomes one elementary particle (at least as Quantum mechanic sees or defines an elementary particle).
Since an elementary particle does not have internal parts, there is no repulsion or attraction inside of the elementary particle. There is nothing inside of an elementary particle, which could repel each other. That is the reason why there is no Coulomb repulsion between two electrons which occupy one quantum state. Please note that this case is very different from the case when two electrons of opposite spins occupy two different quantum states.
Even though their total spin may be zero, they are always two distinguished particles. When distance between two electrons of opposite spins is reduced, the strength of the Coulomb repulsion is reduced from its "normal" value to zero. In case of parallel spins, the strength of the Coulomb repulsion behaves normally: it increases for a shorter distance. The dependence of the Coulomb repulsion on the spin direction and distance between electrons is called the exchange interaction. Please note that the same story can be explained based on a symmetrical and antisymmetric wave function.
I have two papers on this subject:
V. Zayets "Spin rotation after a spin-independent scattering. Spin properties of an electron gas in a solid", Journal of Magnetism and Magnetic Materials 356 (2014)52–67
V. Zayets, "Spin transport of electrons and holes in a metal and in a semiconductor", Journal of Magnetism and Magnetic Materials 445, pp 53–65 (2018) .
The papers are about the spin statistics, but not the exchange interaction. However, both effects are based on the same feature of the time- inverse symmetry, so they could be helpful to understand it.
(why two electrons, which occupy one state, can be considered as one elementary particle)
Q. In the case of two electrons in an atom, they exist in the same quantum energy state (in the same orbital), and in pairs according to the Pauli principle. They do not become one particle. Why don't they become one particle forever? What is the difference ? only distance? And how long should the distance between the two electrons with opposite spin be within approximately in order for them to become one? is it predictable? And I heard that there is an electron-electron interaction between electrons with opposite spin. So when two electrons become one particle as you say, is the electron-electron correlation small enough to ignore? .
Two electrons, which occupy one quantum state, become one elementary particle. Otherwise, the Coulomb repulsion between them would be infinite. This is the origin of the Pauli principle and the reason why two particles can occupy one quantum state despite the infinite repulsion between them. This fact can be understood from the Quantum Mechanic.
Whether the two particles can be called one particle is a matter of definition. However, the definition of an elementary particle is rather fixed in the Quantum Mechanic.
It is important that the elementary subject of the Quantum Mechanic is not the elementary particle, but the symmetry or, to be more precise, the broken symmetry, which is called the Quantum Fields in the Quantum Mechanic. An elementary particle is just a stable state of several broken-symmetries. The degree, of how much the specific symmetry is broken, is fixed for an elementary particle. It is the basic principle of the Quantum Mechanic, which is called the Noether principle. This important principle was well recognized by all founders of the Quantum Mechanic
From this Quantum mechanical point of view, the two electrons, which occupy one quantum state, become one elementary particle, because the quantum state, which they occupy, has one set of several broken symmetries and it is a stable state of a fix number of broken symmetries, which means by definition it is one particle.
(about Remaining Interactions of the elementary particle, which consists of two electrons)
An elementary particle does not have any internal parts and there is no interaction inside of an elementary particle. As a consequence:
----(consequence 1: ) Two electrons of one state are fully undistinguished from each other.
---- (consequence 2: ) Coulomb repulsion: There is none between two electrons.
------(consequence 3: ) Exchange interaction: There is none.
Two electrons, which occupy one quantum state, do not experience any Exchange interaction between themselves or with a neighbor electron. The inner-shell electron does experience any exchange interaction.
------(consequence 4: ) Spin-orbit interaction: There is none.
Neither of the electrons experiences the Spin-orbit interaction. The inner-shell electron does experience any Spin-orbit interaction.
(the fine structure vs. absence of Spin-Orbit interaction)
An exception is an optical transition. The spin-orbit interaction leads to the fine structure.
At the optical transition, one electron transits into the upper energy level and another electron remains in the ground level. Therefore, two electrons are different,the two electrons are not one elementary particle anymore and each electron experiences the spin-orbit interaction individually, which leads to the fine structure in the absorption spectrum of an atom.
Additional complication is that the one-particle state is slightly influenced by the two-separate- electron state . It is a general feature of the Quantum Mechanic. For example in the case of an atom, even though there are no electrons in the excited state, still the excited state slightly influences the ground state. Similarly, even though two electrons in one state is one elementary particle, there is a small influence of its two particle virtual state.
(q1) In the case of two electrons in an atom, they exist in the same quantum energy state (in the same orbital), and in pairs according to the Pauli principle. They do not become one particle.
(a1) Two electrons, which occupy one quantum state, become one particle. It is the origin of the Pauli principle. In this case, all symmetry breaking satisfies the definition of a single particle.
(q2) Why don't they become one particle forever?
(a2) It is a fully- normal quantum state, one or two electrons can be excited to another quantum state. For example, in the electron gas of conduction electrons in a metal, the electron scatterings between the electron states, which occupied by two electrons and which occupied by one electron, occur after 10-100 picosecond after an electron scattered in (for electron energy is near the Fermi energy). For these electrons, the lifetime of the two-electron state is about 10-100 ps.
(q3) What is the difference ? only distance?
(a4) Everything. The wavefunction of two electrons should be absolutely identical. The position, width, energy, wave vector, all should be identical.
(q4) And how long should the distance between the two electrons with opposite spin be within approximately in order for them to become one? is it predictable?
(a4) The distance should be zero in order for two particles to become one elementary particle. Additionally, all other parameters should be absolutely identical (width, energy, wave vector) The Coulomb repulsion between two electrons is reduced when the distance between electrons is reduced. The reduction can be calculated using the classical method of the symmetrical and asymmetrical wavefunctions. It is specific for each quantum state.
(q5) And I heard that there is an electron-electron interaction between electrons with opposite spin. So when two electrons become one particle as you say, is the electron-electron correlation small enough to ignore?
(a5) The electron-electron correlation is for electrons of different quantum states. There is no interaction or correlation inside of an elementary particle, because the elementary particle does not have parts. There might be electron-electron correlation between electrons of different quantum states.
Questions about Order of orbital filling
(about difference of ionization energy between nitrogen and oxygen) )(from Govind) I have read that nitrogen has high ionization energy than oxygen and the reason is exchange energy. Since oxygen have two electrons in same orbital, they will add to make a new particle and there will be no force of repulsion between them so ionization energy of oxygen should be higher because it's difficult to remove a electron from atom when another electron is not repelling it but instead of this my textbook says that there is high repulsion between two electrons in nucleus.
1. Why is there high repulsion in the same orbital (2p) of oxygen?
2. Why is there an exchange interaction between 2p electrons in nitrogen when they have the same spin?
(reason: OFF/ON Coulomb interaction in a half- filled orbital) In a nitrogen atom, there is no Coulomb repulsion between the three 2p3 electrons, distinguishing it from the oxygen atom where there is Coulomb repulsion between the four 2p4 electrons. The positive energy associated with Coulomb repulsion causes the electron energy in the oxygen atom to be significantly higher than that in the nitrogen atom, explaining the observed difference in ionizing energy.
(exchange interaction due to the orbital moment) The presence or absence of Coulomb repulsion is related to the breaking or unbreaking of rotational symmetry. When two electrons of opposite spins occupy one quantum state, they merge into one elementary particle, resulting in no Coulomb repulsion between them. This effect is not a feature of the spin, but the feature of the breaking or unbreaking of symmetry. For example, two electrons of opposite spins can occupy one quantum state, because there is no Coulomb repulsion between them and they literally merge into one elementary particle. Otherwise, the Coulomb repulsion between them would be infinite. This effect is not due to the spins, but due to the breaking/ unbreaking of a symmetry. The spin describes the breaking of the time- inverse symmetry. There are two possible breaking parts. One corresponds to the forward and another part corresponds to backward time flow, , which respectively corresponds to two opposite directions of the spin. Symmetrical vacuum states with no spin can be broken into two parts resulting in two electrons (two particles) with spin-up and spin-down. When these two broken parts (two electrons with opposite spins) combine back together, they restore the state with no spin. This is why there is no Coulomb repulsion between two electrons of opposite spins occupying one state. This breaking and unbreaking of symmetry can apply to other symmetries as well, and the number of broken parts can vary for different symmetries. For rotational symmetry, which is described by the orbital moment, it can be broken into 3 parts (p-symmetry), 5 parts (d-symmetry), or 7 parts (f- symmetry). In the case of oxygen, one 2p state is filled by two electrons, but the Coulomb repulsion disappears only with absolutely identical electrons. Since one state is different, the Coulomb repulsion is restored between all electrons except between two opposite spins. This effect explains why a half-filled orbital is energetically preferred in certain elements like Cr (3d5 4s1), Mn (3d5 4s2), Mo (4d5 5s1), and Tc (4d5 5s2).
(What kind of energy is this exchange energy?)
(exchange interaction as the reason for difference of ionization energy between nitrogen and oxygen) )(from Govind) but still I have some doubts. you didn't answer that why half filled 2p subshell in nitrogen is stable? Since everywhere I have read , I found that exceptionally high stability of half filled subshells are due to exchange energy but how is that possible ? Because exchange interaction ( according to your article) between two electrons is only possible when they have opposite spin but as we know half filled subshells have all electrons with same spin so how they can interact with each other ? "I plan to provide more detailed explanations of this effect on this page." I will be grateful to you if you extend article with some examples like exchange interaction in nitrogen or any other element . Since I just passed high school , I am reading this concept first time and that's why I have some more but very strange questions so only answer them if you find them relevant otherwise just forget about them.
1. First of all What kind of energy is this exchange energy? - electrical, magnetic, nuclear, or anything else that I have not come across yet.
2. When we go across a period let's say from boron to carbon, a electron enters in carbon 2p orbital with the same spin as of another and that leads to release 'exchange' energy so from WHERE DID THAT EXCHANGE ENERGY COME TO ELECTRON?
3. This is last but most ridiculous question. As I have recently read exchange energy is associated to no of changes possible in a subshell for a electron and since highest no of changes are possible for a electron in half filled subshell , that are highly stable. Now let's consider the case when we ionize hydrogen (no exchange energy in hydrogen , since only one electron is there ) by supplying energy to it, electron use that energy to overcome the attraction between the nucleus and itself and comes out of the reach of the nucleus. But In case of nitrogen, outermost valence shell electron releases two kinds of energies when it enters in 2p orbital - (I). Electric potential energy (attraction between electron and nucleus) (II). Exchange energy ( interaction with electrons by changing its position) So when we ionize nitrogen, the electron must gain all the energy that it has released before coming out of the reach of nucleus . It gains electric potential energy by using the supplied energy through breaking the bond between the nucleus and itself but in what form and how it gains exchange energy. This means when an electron gets exchange energy does it stop exchanging its position or does anything else happens to the electron after getting back exchange energy ?
(exchange interaction & forces) The exchange interaction is not a separate field; instead, it is the modulation of already existing fields in a process where two or more electrons combine to form a single elementary particle. The exchange interaction affects all fields, which a particle possesses: the electrical field, the magnetic field and even the gravitational field. The modulation of the electric field due to the exchange interaction is the most influential The exchange interaction affects all fields that a particle possesses, including the electric field, the magnetic field, and even the gravitational field. Among these, the modulation of the electric field due to the exchange interaction is the most influential.
(simple understanding of the exchange interaction) To understand the exchange interaction, let's begin with the simplest and most well-known fact that a single quantum state can be occupied by two electrons with opposite spins. The electrical repulsion force between two particles (in this case, two electrons) with the same charge increases as 1/r^2 as the distance (r) between them decreases. However, when two electrons with opposite spins occupy exactly the same spatial position, the repulsion between them would theoretically be infinite. So, how do they manage to stay at the same point? What force holds them together against this infinite repulsion force? The answer is simple and straightforward: There is no repulsion and there is no electrical field between two electrons of opposite spins occupying one quantum state. The answer is quite straightforward: There is no repulsion and no electrical field between two electrons of opposite spins occupying one quantum state. This is only possible when the two electrons combine and form a different elementary particle. An elementary particle does not have internal parts, so there is no internal repulsion within it, and thus, no interaction between parts.
(how do particles combine into another particle) The most known example of this is the interaction of a particle and antiparticle, for example, an electron and a positron. As a result of this interaction, both the electron and the positron ceased to exist. They combined to become a new quantum state: the vacuum state or nothing. In the case of a particle and its antiparticle, all their properties, such as charge and spin, are opposite. However, there are instances where only one property of the two particles is different, like their spin or orbital moment. When these particles interact, only that specific property ceases to exist, while the other properties remain unchanged. As a result, the outcome of the interaction is not the vacuum state but an elementary particle with one less property (e.g., no spin or no orbital moment). Each property of an elementary particle, such as its charge, spin, or orbital moment, corresponds to a specific broken symmetry. When particles combine to form another elementary particle, one of these broken symmetries becomes unbroken. For example, when two electrons with opposite spins combine, the resulting electron has no spin.
(exchange interaction due to the orbital moment vs. exchange interaction due to the spin) The exchange interaction specifically takes place between electrons where only one parameter is opposite. This parameter does not necessarily have to be the spin; it could be any other property. For instance, the exchange interaction can also be attributed to the orbital moment. While the exchange interaction due to spin is more commonly known, the exchange interaction due to the orbital moment plays a crucial role in the process of atomic orbital filling, despite being less well-known.
(spin: exchange interaction between 2 electrons vs. orbital moment: exchange interaction between 3 or 5 or 7 electrons ) Each property of a particle corresponds to a specific broken symmetry. Some symmetries, such as the charge and spin, are broken into only two parts, while others are broken into more parts. For instance, the p-orbital moment has three parts, and the d-orbital moment has five parts. When these opposite parts combine together, they either annihilate each other or become the vacuum or zero state. For example: Charge "+" + Charge "-" = 0 (nothing) Spin "up" + Spin "down" = 0 (nothing) However, to obtain a zero state with the p-orbital moment, it is necessary to combine three p-orbital moments: p-orbital 1 + p-orbital 2 + p-orbital 3 = 0 (nothing) Similarly, it takes five electrons of different d-orbitals to form a zero state: d-orbital 1 + d-orbital 2 + d-orbital 3 + d-orbital 4 + d-orbital 5 = 0 (nothing) As a result, the exchange interaction occurs only between three electrons of different p-orbitals or between five electrons of different d-orbitals. This is in contrast to the case when the exchange interaction occurs only between two electrons of different spins.
( The reason why the half- filled orbitals are very stable) The energy of a state occupied by two electrons with opposite spins is low because there is no repulsion force between them, resulting in a positive repulsion energy of zero. A similar principle applies to the exchange interaction due to the orbital moment in half-filled orbitals. For example, in the case of three p-electrons occupying one quantum state in a half-filled p-orbital, there is no repulsion between them, and the energy of this state is at its lowest. Likewise, when five d-electrons occupy one quantum state in a half-filled d-orbital, there is no repulsion between them, leading to the lowest energy state.
(The reason why the exchange interaction due to the orbital moment is larger than the exchange interaction due to the spin) When one of the two electrons is removed from a quantum state filled with electrons of opposite spins, the energy increases because the repulsion between the two electrons is restored. Similarly, when one of the three electrons is removed from the half-filled p-orbital, the energy increases even more because the repulsion between the three electrons is restored. Consequently, the increase in positive energy is greater in this case, making the half-filled p-orbital more stable than the state filled with electrons of opposite spins. Likewise, when one of the five electrons is removed from the half-filled d-orbital, the energy increases significantly because the repulsion between the five electrons is restored. The hike in positive energy is substantial in this case, leading to the extreme stability of the half-filled d-orbital.
(exchange interaction between electron and nucleus on the consequence of the orbital filling) There is no exchange interaction between the electron and the nucleus, and the attraction force between them is completely spin-independent. The exchange interaction can only occur between very similar and nearly identical objects. Since the electron and the nucleus are different entities, they do not have any exchange interaction between them. However, there is an indirect exchange interaction between the electron and nucleus in a solid, which is the only known source of the ferromagnetic exchange interaction and is responsible for ferromagnetism in metals like Fe, Co, and Ni. This indirect exchange interaction occurs not because the attractive force between the electron and the nucleus is spin-dependent, but rather because the electron's position is influenced by neighboring electrons. The electron's position with respect to the nucleus is influenced by neighboring electrons, which can push it either closer or farther away from the nucleus. This, in turn, affects the strength of the attraction between the electron and the nucleus. Since this interaction with neighboring electrons is spin-dependent, the pushing effect on the electron's position becomes spin-dependent as well. Consequently, the attraction force between the electron and the nucleus becomes spin-dependent due to this spin-dependent pushing from neighboring electrons. At this moment, I do not see how such an indirect exchange interaction between the electron and nucleus is possible for the orbital filling. However, it is possible that future research may uncover some pathway for such an interaction.
(orbital exchange interaction as the reason for difference of ionization energy between nitrogen and oxygen) )(from Govind) I'm encountering some challenges in achieving a complete understanding of the intricate concepts you've outlined "When one of the two electrons is removed from a quantum state filled with electrons of opposite spins, the energy increases because the repulsion between the two electrons is restored. Similarly, when one of the three electrons is removed from the half-filled p-orbital, the energy increases even more because the repulsion between the three electrons is restored. Consequently, the increase in positive energy is greater in this case, making the half-filled p-orbital more stable than the state filled with electrons of opposite spins." You are saying that repulsion energy in p subshell filled with 3 electrons of same spin (e.g. Nitrogen) is more than a orbital filled with 2 electrons of opposite spin (e.g. Oxygen ), but it contradictory to the fact that it is more difficult to pull a electron out of 3 electrons filled p orbital ( e.g. Nitrogen ), because if (according to you ) there is more repulsion between electrons in p orbital then it will easier to get a electron out of nitrogen than oxygen. "the increase in positive energy is greater in this case, making the half-filled p-orbital more stable than the state filled with electrons of opposite spins." This statement is again confusing me because a system is stable when it has negative energy like a electron in atom is stable due to negative binding energy between nucleus and electron itself , so how can you say that increase in positive energy results in higher stability.
Convid, I am sorry. There was a typing mistake. Of course, the orbital exchange interaction between 3 p- electrons of nitrogen is larger than the spin- exchange interaction between 2 electrons of oxygen.
(strength of exchange interaction & forces) Short answer for the reason why the half- filled orbitals are very stable is because there is no Coulomb repulsion between any of the electrons in the half- filled orbital. There is no repulsion, because the rotation symmetry, which is described by the orbital moment, is unbroken. When the Coulomb repulsion is stopped for more electrons, the more stable the orbital becomes. For example, the half- filled d- orbital is more stable than the half- filled p- orbital.
Due to filling the spin, the repulsion only between two electrons is stopped. Due to filling the orbital moment, the repulsion between three or five or seven electrons is stopped. Therefore, the exchange interaction, because of the orbital moment, is always stronger than the exchange interaction due to the spin. For this reason, the energy of the nitrogen atom, in which repulsion between three electrons is stopped due to the unbroken the orbital symmetry, is lower than the energy of the oxygen atom, in which repulsion between only between two electrons is stopped due to the unbroken the spin symmetry.
Q. , after some time of pondering I remembered about Hund’s rule and stuck in confusion why it would work if the electrons with antiparallel spins don’t repel each other on short distances. At first sight, electrons would always “want" to occupy as little orbitals as possible and make total spin go to zero. So my idea is that it maybe Hund’s rule work because of the energy barrier imposed by electron interaction, because even if the spins are antiparallel they repel until some point, and then the repelling diminishes. I couldn't find approval of that, in fact all the articles about “real” explanation of Hund’s rule available involve some complicated QM which, to my bad, I am not yet acquainted with. Also, in case my intuition is close to the truth, it may be then possible to somehow “force” an additional electron to pair up instead of occupying new orbital. For example, if we send the electron with just the right speed to, say, C+ particle, it may be stuck at the paired up stated and be stable since in this case it would be attached to the nucleus more tightly. I haven’t done any calculations and understand that there may be no possibility for that in case there is no such theoretical range of energies-electron speed, but maybe it would be possible if we could do calculations with different atoms. A. The mechanism that leads each electron, as it fills a vacant orbital, to align its spin parallel to other electrons is the orbital-type exchange interaction. The orbital-type exchange interaction forces all spins within the same half- orbital to align in a parallel.
The orbital-type exchange interaction is the strongest interaction and it mainly determines the filling role for the orbitals.
( three effects governing orbital filling): Dependency of orbital occupancy on the electron spin direction is determined by three effects: (1) orbital- type exchange interaction (strongest); (2) spin- type exchange interaction (moderate) and the spin-orbit interaction.(weakest)
The orbital- type exchange interactions is forcing electron spins to align parallel each other. The spin- type exchange interactions is forcing electron spins to align anti parallel each other. The the spin-orbit interaction is forcing electron spins to align parallel each other. Reason why:The exchange
The exchange interaction is originated from the feature of our Nature that the state of a higher symmetry has a lower energy. The reason why the energy is lower is that the interaction between two particle disappears when two particle join each other to create a single particle of a higher symmetry.
An example is two electrons of opposite spins. For each electron, the time-inverse symmetry is broken and the wavefunction is a spinor. When these two electrons of opposite spins occupy one quantum state, they become one single new particle with charge of -2e and no spin. The time-inverse symmetry for this new particle is not broken and its wavefunction is a scalar.
This new particle is not a simple sum of two electrons of opposite spins. For simple sum of two electrons of opposite spins, the time- inverse symmetry is not broken!. For example, two opposite spins can be directed along the x- axis or the y-axis or the z-axis. Therefore, two electrons of opposite spins occupying one state is really a new particle. It is absolutely not a the sum of two individual particles, which are sitting in one place.
An elementary particle does not have parts. Therefore, there can not be any interaction between nonexistent parts of elementary particle. That is why the Coulomb interaction between charges of two electrons of opposite spins is switched off when two electrons approach each other.
The symmetrical and asymmetrical wavefunction, which are used to describe the exchange interaction, just describe the process how two individual particles are monotonically transformed into one particle as two electrons approach each other.
The spin-orbit interaction is just the magnetic field of a relativistic origin, which is forcing all electron spins to align along its own direction. The spin-orbit magnetic field is induced by an electrical field of the nucleus due the finite speed of the electron orbital movement.
When an electron moves in electrical field, it experience a magnetic field. It is a relativistic feature of the electromagnetic field. The similar relativistic effect is Lorentz force: .When an electron moves in a magnetic field, it experience an electrical field, which forces the electron to turn from a straight movement.
(from YWK) Why don't the electrons at the same quantum state in an atom (coulomb potential), such as a oxygen atom or a nitrogen atom, be on particle?
The examples of cases when two or more electrons behave as one particle is (1) a quantum state filled by two electrons of opposite spin, (2) orbitals of an inert gas, (3) inner orbital shells of atoms, (4) half- filled shells, like that of nitrogen.
(from YWK) Conversely, under what conditions can one particle be?
When one of particle symmetries is unbroken. For example, the spin describes the broken time- inverse symmetry. The time- inverse symmetry is not broken for a state occupied by two electrons of opposite spins. Another example is a very stable half- filled orbital (e.g. of nitrogen). For this orbital, the rotation symmetry is not broken.
(from YWK) >I think that one particle is possible in a quantum well. Under what conditions possible within the quantum well?
Yes, for example, when a state of the quantum well is filled by two electrons of opposite spins. It is the case of a semiconductor- made quantum well when the Fermi level is close to the conduction band.
about polarity of exchange integral, about the reason why the exchange interaction changes from antiferromagnetic to ferromagnetic.
(from SAROJ KUMAR MISHRA) Q. In the exchange interaction energy equation there is an exchange integral term Jex. so the question is that, if Jex is positive then why all the spins will be aligned parallel, and if Jex is negative then why all the spins will be aligned antiparallel
The exchange integral is only a mathematical trick to somehow describe the exchange interaction. The reason, for which it is introduced, is so that minimizing the total energy gives either ferromagnetic (parallel) or antiferromagnetic (antiparallel) spin alignment. Only for this reason, the exchange integral is either positive or negative. In fact, the physics of the exchange is more rich, complex and interesting. In order to understand it and, therefore, the polarity of the exchange interaction, let me explain it for a set of electrons aligned in a 1D line. The Coulomb interaction between two neighbor electrons depends on the mutual spin directions. The repulsion between electrons is largest when their spins are parallel and is smallest when their spins are anti parallel. Since the energy of the repelling is positive, the minimum of the energy corresponds to antiparallel alignment of spins, negative exchange integral and the antiferromagnetic exchange interaction. I would like to emphasize that the exchange interaction between two electrons is always antiferromagnetic and therefore the exchange integral is always negative. If in the previous example there were only electrons, in the next example, additionally there are positively-charged nucleus at the position of each electron. There is no exchange interaction between nucleus and the electrons. There are inner-shell electrons and the electron under consideration occupies the external shell, which is relatively far from the nucleus. The energy of the attractive Coulomb interaction between electron and nucleus is negative and its absolute value is larger when the distance between electron and nucleus is shorter. The repelling Coulomb force from the left and the right neighbor electrons forces to shrink the electron orbital pushing the electron closer to the nucleus and, therefore, makes smaller the energy of the Coulomb interaction between the electron and the nucleus .Therefore, the repulsion between each two neighbor electrons has two opposite contributions to the total energy. The energy increases due to an increase of the repulsion Coulomb energy between two electrons and the energy decreases due to a decrease of the attraction Coulomb energy between the electron and the nucleus. When the latter prevails, the increase of the repulsion between neighbor electrons causes a decrease of the total energy. Since the repulsion between neighboring electrons is larger when their spins are parallel, the total energy is smaller for the parallel spins, the exchange is ferromagnetic and the exchange integral (the addition to the total energy) is positive. Note: the identical result can be obtained considering the symmetrical and anti symmetrical wavefunctions.
(to conclude):
The exchange interaction between two electrons is always negative. It is because of the fundamental property of the broken time inverse symmetry. The exchange interaction occurs because the degree of the broken time- inverse symmetry for a system of two electrons decreases when the distance between them decreases. As a result, the strength of the Coulomb interaction becomes spin-dependent.
When additionally the electron interacts with a nucleus or other electrons, the exchange may become ferromagnetic. It is because the spin- dependent reduction of the repulsion between two electrons may reduce the attraction between the nucleus and the electrons or may increase repulsion between the electron and other electrons. Each process leads to the lower total energy for parallel spin alignment and the ferromagnetic exchange interaction.
The spins are aligned into the directions when the total energy of their interaction is smallest. Otherwise, there is a precession of the spin and, therefore, there is a precession of the magnetic moment, which causes an emission of a circularly- polarized photons and the reduction of the total energy until the energy minimum. See details here.
Q. Is it possible that an elementary particle without charge be a fermion? A. No. Only charged particles can be fermions. The Majorana fermion can not exist.
Only one fermion (or two fermion with opposite spins) can occupy one quantum state. In order for an elementary particle to be a fermion, there should be a force, which prevents two or more fermions to occupy one quantum state. In case of a charge particle, the Coulomb repulsion prevents two or more identical particles be at the same place at the same time (occupy the same quantum state).
There should be some force, which repels fermions from each other to prevent occupation of a quantum state by two fermions. The force should be one from known forces of the nature. There is no any "special" "quantum-mechanical" force to do this.
Relation between precession damping and exchange. Spin relaxation: individual or collective?
( from Sky) Q. I have some confusion about the pressesion damping for the localized electrons. There are two statements in this subject: (1)"All localized electrons are aligned to each other due to the strong exchange interaction. The spins of these electrons are spatially localized to the size of about one atom. As a result, the spins of neighbor electrons swing with respect to each other (similarly as balls connected by springs)." and (2) "In case of localized electrons, the spin damping is the individual process when each electron experiences the spin damping individually and independently from other localized electrons." In my opinion, the statement (1) means that the pressesion damping of localized electrons is strongly connected with each other, which seems contradict with statement (2).
The spin precession and the precession damping are a collective effect, when the directions of all spins are parallel all the time. It is because the exchange interaction between spins is very strong. Exceptions are the spin waves and domain walls. The exchange interaction between localized neighbor electrons is very strong, but is not infinitely strong. As a result, a slight misalignment between neighboring spins are possible (spin waves). Also, when some strength is accumulated over many spins (over millions or billions of spins) the parallel alignment between neighboring spins can be broken (a domain wall).
The spin damping is a collective process of the total spin. There is no individual spin damping. The spin-down to spin-up quantum transition of one electron means only change of one component of the total spin and is not related to individual spin of one localized electron.
Since the exchange interaction is not infinitely strong, a slight misalignment between two localized neighbor electrons is possible. Due to such a tiny misalignment, a spin wave exists in a ferromagnetic material. A spin wave is a mixture of an electromagnetic wave and spin precession. The magnetic component of an electromagnetic wave is slightly different at a position of each localized electron. As a result, the spin precession is slightly different between neighboring localized electrons. As you said, the spins of neighboring electrons slightly swing with respect to each other. Even though the spin misalignment between neighboring electrons is very small and the spins of neighboring electrons are still nearly parallel, the misalignment is accumulated with a distance and can be substantial for the electrons separated by a long distance.
(spin wave as a source of the spin damping)
The spin wave is a particle with a non-zero spin. It interacts with the total spin of the nanomagnet causing an electron transition from the higher- energy spin-down energy level to the lower- energy spin-up energy level. This process is called the spin damping and this quantum transition is fully equivalent to the classical precession damping. It is important that the spin wave interacts with the total spin of the whole nanomagnet, but not with individual spin of localized electrons. The interaction is the most efficient when the size of the nanomagnet or size of a magnetic domain matches the wavelength of the spin wave.
(strength of the exchange interaction)
The strength of the effective exchange magnetic field is possible to estimate from Curie temperature (see above). The magnetic field of the exchange interaction is rather high. It is about 1900 Tesla for Co and 900 Tesla for Ni. For example, a large superconducting magnet produces a magnetic field of about 20-40 Tesla. Because of the high strength of the exchange interaction, it is nearly impossible that the spin of one individual localized electron is reversed with respect to the spin direction of all neighboring electrons. Only many electrons can reverse their spins simultaneously and coherently ( a magnetic domain)
(spin dumping for an individual electron)
All individual localized electrons are so strongly glued to each other by the exchange interaction, they behave as one quantum object. Spin of a localized electron is aligned strongly to be parallel to the spins of its neighboring localized electrons. The total spin behaves as one quantum object. It precesses as one object or tilts its direction as one object and interacts with spin waves (magnons) and circularly- polarized photons as one object.
(spin of one individual electrons vs. the spin as a component of the total spin)
Even when there is a quantum transition of an electron from the spin-down to spin-up energy level (spin damping), it does not mean that one localized electron becomes spin-up in the surroundings of neighboring spin- down electrons. The spins of all neighboring electrons remain parallel (nearly) all the time. The meaning of the transition of one electron from the spin-down to spin-up energy level means that one component of the total spin is changed and, as a result, the precession angle of the total spin becomes larger. All the time the spin of all localized electrons are glued to each other. All spins precess coherently and are always parallel to each other.
(magnetic domain & spin damping)
The strong exchange interaction can be broken at a boundary between magnetic domains. Some effects can accumulate for a larger number of localized electrons. When the number of localized electrons reaches some critical number, a domain wall is formed. The behavior of two neighbor domains may be rather independent. E.g., the magnetic dipole interaction makes magnetization of neighbor domains to be antiparallel. Similarly, the spin precession of the neighbor domains can be at slightly different frequency and the precession angle.
I will try to answer your questions as soon as possible
