() (interface roughness & SO ): Why does interface roughness influence the strength of spin-orbit interaction?

() (interface roughness & demagnetization ): Why does interface roughness influence the strength of demagnetization field?

() (smoother interface & demagnetization): Why is the demagnetization field larger for a smoother interface?

() Questions about oscillations of the strength of spin- orbit interaction

() about oscillations of the strength of spin- orbit interaction

() (origin of SO oscillations) : What causes the oscillations in the strength of spin-orbit interaction with an increasing external magnetic field?

() Hso vs. Hext -> linear dependence or oscillations?

() about measurements of SO oscillations

() Questions about Variation of Magnetic Anisotropy and Strength of Spin-Orbit Interaction on Magnetization Reversal

() about possible influence of hysteresis, remaining domains

() about possible mechanism of SO dependence on magnetization reversal

.........

my publications on measurements of strength of spin- orbit interaction:

Basic: Zayets "Peculiarities of spin-orbit interaction systematically measured in FeCoB nanomagnets" (2024)

under gate voltage: Zayets "Features and Peculiarities of Gate-Voltage Modulation of Spin-Orbit Interaction in FeCoB Nanomagnets: Insights into the Physical Origins of the VCMA Effect" (2024)

(video): Measurement of coefficient of spin- orbit interaction in a nanomagnet.
(Part 1a): Spin-Orbit (SO) interaction. Perpendicular Magnetic Anisotropy (PMA)   (Part 1c): Internal magnetic field in a nanomagnet   (Part 2): Measurement method of Spin-orbit interaction (SO)  & Perpendicular Magnetic Anisotropy (PMA)   (Part 5a): Analyze of anisotropy field Hani. Measurement of coefficient of spin-orbit interaction kSO       (short content 1:)  the properties of spin-orbit interaction   (short content 1:)  the difference between Global, Local & Average Magnetic Fields.   (short content 1:)  how it is possible to measure  the strength of SO and strength of PMA.    (short content 1:) analyze the measurement of the anisotropy field (short content 2:)   linear relation between the external magnetic field and Hso and about the symmetry and physics arguments, which are behind this linear relation   (short content 2:)  how to measure experimentally the internal magnetic field Hint   (short content 2:)    what holds  the magnetization along the easy magnetic axis and how to measure the strength of the holding force.   (short content 2:)  the measured oscillations of Hani and why this oscillation is an important characteristic of a nanomagnet (short content 3:)   how the deformation of the orbital at the interface creates the perpendicular magnetic anisotropy (PMA)   (short content 3:) experimental measurements of Hint in FeB nanomagnets.   (short content 3:)   the experimental setup and main idea behind the proposed measurement   (short content 3:)   why the spin-orbit interaction depends on the polarity of the magnetic field and how to measure it.
Other parts of this video set is here
click on image to play it

Measurement of strength of spin-orbit interaction in FeCoB nanomagnet

Coefficient of spin-orbit interaction kSO is a measure of strength of the spin- orbit interaction
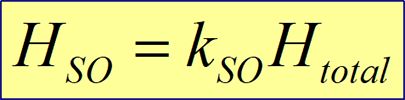Only parameter, which describes the strength of spin- orbit interaction, is the magnetic field Hso of spin- orbit interaction. The strength of Hso is proportional to the total applied magnetic field Htotal. The proportionality coefficient is called the coefficient of spin- orbit interaction and which gives the strength of the spin- orbit interaction.
The total applied magnetic field is the sum of intrinsic and external magnetic field.

Which parameter defines the strength of the spin- orbit interaction?

The coefficient of spin-orbit interaction k_SO, which gives the strength of the spin- orbit interaction. k_SO is the proportionality coefficient between the magnetic field Hso of spin- orbit interaction and the total applied magnetic field Htotal (internal plus external magnetic fields).

(note): Only parameter, which describes the strength of spin- orbit interaction, is the magnetic field Hso of spin- orbit interaction.

Measurement Method of the strength of spin- orbit interaction. In short.

Measurement of strength of spin-orbit interaction
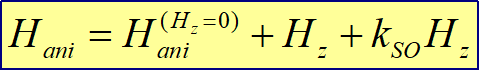Eq. 45. Anisotropy field Hani is linearly increases when an external magnetic field Hz is applied along the magnetic easy axis. The proportionality coefficient between Hani and Hz is the coefficient of the spin orbit interaction kSO.
(measurement method) The anisotropy field Hani is measured as a function of an external magnetic field Hz applied along the magnetic easy axis. The proportionality coefficient gives kSO
(math) The detailed math of how to obtain this equation is here

The measurement of the strength of the spin- orbit interaction is relatively simple and straightforward.

The magnetic field of spin-orbit interaction Hso holds the magnetization along the magnetic easy axis. A measurement of how strongly the magnetization is held along its easy axis evaluates the strength of the spin- orbit interaction.

For this purpose, an external magnetic field is applied along the hard axis and, therefore, perpendicular to the easy axis forcing the magnetization to tilt out from the easy axis. The stronger the spin- orbit interaction is, the harder it is to tilt the magnetization.

The anisotropy field is a magnetic field, at which the magnetization is fully tilted along the hard axis, and is a good measure of the spin-orbit interaction.

If additionally an external magnetic field is applied along the easy axis, the spin- orbit interaction becomes stronger and, correspondingly, the anisotropy field becomes larger. As you can see, the anisotropy field is linearly proportional to the strength of the spin-orbit interaction. Therefore, a measurement of anisotropy field versus the external field,gives the strength of the spin- orbit interaction.

Measurement of strength of spin-orbit interaction
Two magnetic fields are independently controlled in this measurement. The in-plane magnetic field Hx is applied in-plane and, therefore, perpendicularly to the easy axis. Hz is applied along the easy axis.
(measurement method) For each fixed Hz, Hx is scanned and the magnetization tilting angle is measured. From this dependence, the value of Hani is evaluated for each Hz. From linear dependence Hani vs. Hz, kSO is evaluated

(key feature of the measurement): Two magnetic fields (along Hz and perpendicular Hx to the easy axis) are applied and independently controlled

(measurement method)

(step 1): For each fixed Hz, Hx is scanned and the magnetization tilting angle is measured.

(step 2): From the dependence of H_ani vs. Hx, the value of H_ani is evaluated for each Hz.

(step 3):From linear dependence H_ani vs. Hz, k_SO is evaluated

Fig.41. Examples of experimental measurements of strength spin-orbit interaction
Nanomagnet with a single ferromagnetic layer   Nanomagnet with a single ferromagnetic layer   Slope is small and negative and, therefore, kSO is negative and small.   Slope is large and positive and, therefore, kSO is positive and large. There are only 2 interfaces: FeB/Ta & FeB/MgO. The positive contribution to SO strength of interface is not sufficient to overcome the negative contribution from the bulk. As a result, kSO is negative and small   There are a total of 10 interfaces: FeB/W, FeB/Ta, and FeB/MgO. Each of these interfaces contributes to the enhancement of the spin-orbit interaction strength. Consequently, the value of kSO becomes significantly large and positive.
(interface & bulk contributions): The strongest and positive contribution to the strength of spin- orbit interaction is from interfaces. The bulk contribution is small and negative. As a consequence, kSO is small in a single- ferromagnetic- layer nanomagnet, which has only two interfaces and in which the interface contribution is comparable to the bulk contribution, and is large in a multi- layer nanomagnet, which has many interfaces and in which the interface contribution dominates.
(oscillations): There are clear oscillations on top of the linear dependence. The oscillation is due to a periodic dependence of spin- orbit interaction on the magnetic field. The oscillation is a feature of an interface and is stronger when interface contribution is larger and the bulk contribution is weaker (See below)
(two measured parameters): A linear fitting of this dependence gives two parameters: (parameter 1) slope of the line, which gives coefficient of spin- orbit interaction kSO. (parameter 2): offset of the line, which gives the anisotropy field in absence of an external field or simply the anisotropy field Hani.
click on image to enlarge it

Relation between anisotropy field H_ani, strength of spin- orbit interaction k_SO & demagnetization field H_demag

Relation between spin-orbit interaction and anisotropy field
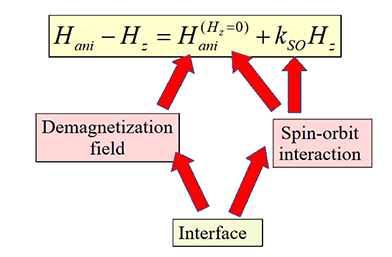When some conditions at a nanomagnet interface are changing, it affects both the strength of spin orbit interaction kSO and demagnetization field Hdemag. Since the anisotropy field Hani depends on both kSO and Hdemag, the anisotropy field changes as well. However, the polarity change of Hani may be different according to whether the kSO or Hdemag contribution to anisotropy field is dominated for the specific nanomagnet.
When polarity of change of Hani is the same as that of kSO, the spin- orbit contribution dominates.
When polarity of change of Hani is opposite to that of kSO, the demagnetization contribution dominates.
click on image to enlarge it

There are two parameters, which are evaluated from the measured linear dependence of Fig.41: (parameter 1): coefficient k_SO of spin orbit interaction (the slope of the line) and (parameter 2): anisotropy field in absence of external field or simply the anisotropy field H_ani ( the offset of the line)

Both k_SO and H_ani depend on a variety of nanomagnet parameters such as interface roughness, nanomagnet thickness, current, gate voltage etc.

It is important, the dependencies of k_SO and H_ani are not independent.

(reason):

The anisotropy field is proportional to the strength of the spin- orbit interaction and the internal magnetic field Hint:

The internal magnetic field is the field along the magnetization M minus the demagnetization field H_demag and plus the magnetic field of spin- orbit interaction H_SO:

Therefore, the anisotropy field is proportional to the coefficient of spin-orbit interaction and the demagnetization field:

(note) Usually k_SO and H_demag increase or decrease simultaneously. As a consequence, the anisotropy field H_ani can either increase or decrease depending which contribution k_SO or H_demag to H_ani is larger

Factors, which affect k_SO and H_demag:

(factor 1): interface roughness (see below)

(rougher interface) → (k_SO is smaller) & (H_demag is smaller) ⇒ (H_ani is either smaller or larger)

The dependence of on the interface roughness is different for a nanomagnet containing one or several ferromagnetic layers.

a single-layer nanomagnet: (rougher interface) →(H_ani is smaller)

a multi-layer nanomagnet: (rougher interface) →(H_ani is larger)

(factor 2): nanomagnet thickness (see below)

when k_SO contribution is positive for interface and negative for the bulk

(thicker nanomagnet) → (k_SO is smaller) & (H_demag is the same) ⇒ (H_ani is smaller )

(factor 3): polarity of applied magnetic field (see below)

only in the case of asymmetrical nanomagnet

(larger change with reversal of H) → ( Δk_SO is larger) & (ΔH_demag is the same) ⇒ (ΔH_ani is larger )

(factor 4): Electrical current. SOT effect (see below)

(a larger current) → (k_SO is ) & (H_demag is ) ⇒ (H_ani is )

(factor 5): Gate voltage. VCMA effect (see below)

(a larger positive gate voltage) → (k_SO is larger) & (H_demag is smaller) ⇒ (H_ani is smaller)

Internal magnetic field H_int

Measurement of internal magnetic field
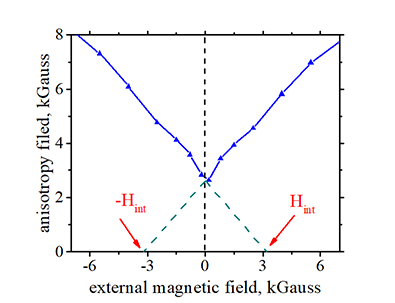Extending measured linear dependence of anisotropy Hani vs. external magnetic field Hz till value Hani=0, gives the value of the internal magnetic field Hint
The case Hani=0 corresponds to the case when there is no magnetic anisotropy and, therefore, when the anisotropy field equals zero and when there is no internal field.
click on image to enlarge it

The magnetic field, which holds the magnetization along its easy axis, is called the internal magnetic field.

(fact) The measured internal magnetic field in a FeCoB nanomagnet is in range between 2.5-5 kG. However it can be as large as 15 kG in a single- layer FeCoB nanomagnet and can be less than 1 kG in a multilayer nanomagnet.

(how to measure the internal magnetic field)

Extending measured linear dependence of anisotropy H_ani vs. external magnetic field H_z till value H_ani =0, gives the value of the internal magnetic field H_int

The anisotropy filed depends linearly on the external magnetic field H_z, which is applied along easy axis

In absence of external magnetic field H_z, only the internal magnetic field H_int holds the magnetization along the magnetic easy axis and the anisotropy field is linearly proportional to the internal magnetic field Hint. Since both the external and internal magnetic field are just the magnetic field and, therefore, should have the similar force on the spin, Eq. (41.1) can be written as

Similar to the external magnetic field H_z, the internal magnetic field H_int also has the bulk contribution, which should be considered. Then, correct form of Eq. (41.2) would be

Comparison of Eqs (41.1) and (41.2) gives the internal magnetic field H_int as

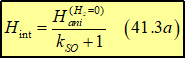
In the case when there is no external magnetic field H_z =0 and no internal magnetic field H_int=0, the anisotropy field eqauls zero (See Eq. 41.2a) and there is no magnetic anisotropy

(fact) In vacuum, there is no magnetic anisotropy. Therefore, the anisotropy field equals zero and there is no internal field.

Measured internal magnetic field in FeCoB nanomagnets	Samples. Thickness in nm shown in blankets
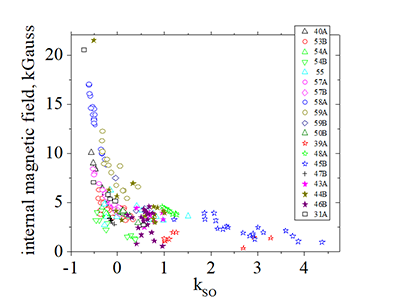Fig 44 The internal magnetic field vs. coefficient kSO of spin- orbit interaction systematically measured in FeCoB nanomagnets of different thickness, size, structure, composition.	Dots of the same color and shape correspond to nanomagnet fabricated at different places of the same wafer. Stars show multilayer nanomagnets, which contain several ferromagnetic layers.
The internal magnetic field is stronger for single- layer nanomagnets and weaker for multi-layer nanomagnets (shown by stars).	The nanomagnet of a different width and length in range from 50 x 50 nm to 3000 nm x 3000 nm are shown.

Three contributions to the internal magnetic field H_int:

(contribution 1) : Magnetic field along magnetization M

(contribution 2) : Demagnetization field

(contribution 3) : Magnetic field H_SO of the spin-orbit interaction

(fact) The electrons in the bulk of a nanomagnet and at the interface experience a very different internal magnetic field H_int, because they experience a very different magnetic field H_SO of the spin-orbit interaction

Factors, which affects the strength the internal magnetic field H_int:

(factor 1) : Magnetization M

A nanomagnet, which has a larger magnetization, often has a larger H_int, because of larger contribution 1. However, other factors can reverse this tendency.

(factor 2) : Magnetic anisotropy. Anisotropy field H_ani

A harder nanomagnet has a larger H_int. The anisotropy field H_ani is linearly proportional to the internal magnetic field H_int

(factor 3) : Roughness and sharpness of an interface

Both the demagnetization field and the magnetic field of Spin-orbit interaction substantially depend on the perfection of the interface.

(factor 4) : Thickness of a nanomagnet

The strength of spin- orbit interaction is substantially different for the electrons in the bulk of a nanomagnet and at the interface. The bulk contribution is stronger for a thicker nanomagnet and the interface contribution is stronger for a thinner nanomagnet

(factor 5) : Structure of a nanomagnet

The demagnetization field is substantially in a multilayer nanomagnet than in a single layer nanomagnet. As a consequence, the internal magnetic field in a multilayer nanomagnet is smaller than in a single layer nanomagnet. This is because the effect of interfacial imperfections, which reduces the demagnetization field, is less prominent in a multilayer nanomagnet.

Why is the internal magnetic field in a multilayer nanomagnet substantially smaller than in a multi- layer nanomagnet?

It is because of a larger demagnetization field. The larger the number of interfaces is, the more efficiently the demagnetization field is created. In an ideal non- existed case of 100% efficiency of creation of the demagnetization (e.g. ideally- smooth ideally- planar ideally- sharp interface), the demagnetization field exactly equals the magnetization field and, as a consequence, the internal magnetic field becomes zero.

Excluding the free-space contribution

free-space contribution to Hani
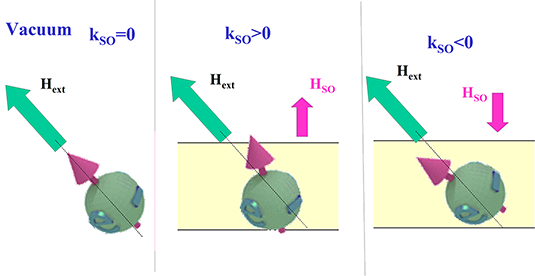(left) In vacuum, the spin is always aligned precisely along the external magnetic field. In a nanomagnet, the magnetic field HSO of spin- orbit interaction tilts the spin out of the direction of the external magnetic field Hext
(center) When the coefficient kSO of spin-orbit interaction is positive, the spin is tilted towards the surface normal. (right) When the coefficient kSO of spin-orbit interaction is positive, the spin is tilted towards the in-plane direction.
click on image to enlarge it

The origin of the free-space contribution to H_ani is the simple and obvious fact that in vacuum the spins always align perfectly along the magnetic field.

(fact): Because of the free-space contribution, the dependence of H_ani -H_z vs. H_z is more informative than the dependence of H_ani vs. Hz

In vacuum, the spin is always aligned exactly along the external magnetic field.

In a nanomagnet, the external field also creates the SO magnetic field.

When this field is directed along an external field, k_SO is positive.

When SO field is directed opposite to external field, k_SO is negative

Excluding free-space contribution
with free- space contribution
sample 1   sample 2   wafer VOLT 58A Ta(5 nm)/ (FeCoB 1 nm, x=0.3) (see here) nanomagnet L43C SOT   wafer Volt46B W(3):[FeB(0.68)/W(0.25)]x4/ FeB(0.68) nanomagnet free18.
The presence of non-informative free-space contribution masks crucial properties embedded within this measured dependence. These properties include the slope of the line, which directly relates to the strength of the spin-orbit interaction, as well as the oscillations and disparities observed during magnetization reversal.
without free space contribution
sample 1   sample 2   wafer VOLT 58A Ta(5 nm)/ (FeCoB 1 nm, x=0.3) (see here) nanomagnet L43C SOT   wafer Volt46B W(3):[FeB(0.68)/W(0.25)]x4/ FeB(0.68) nanomagnet free18.
Upon eliminating the non-informative free-space contribution, the polarity and strength of the spin-orbit interaction (reflected by line slopes), the amplitude and period of oscillation, and the distinctions arising from magnetization reversal become distinctly visible and unequivocally clear.
click on image to enlarge it

Oscillations of the strength of spin- orbit interaction under an external magnetic field

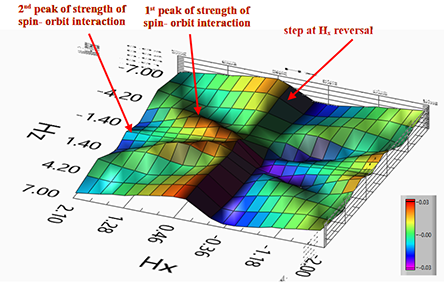
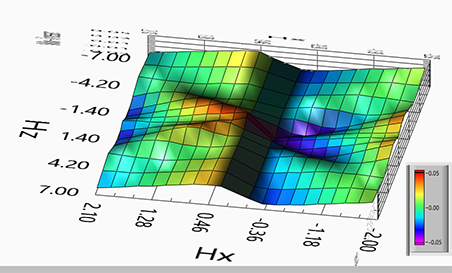
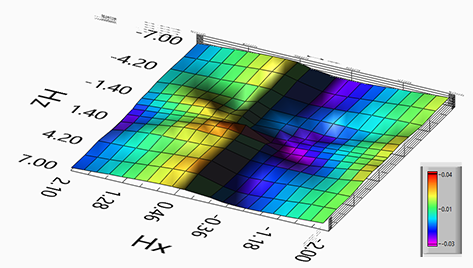
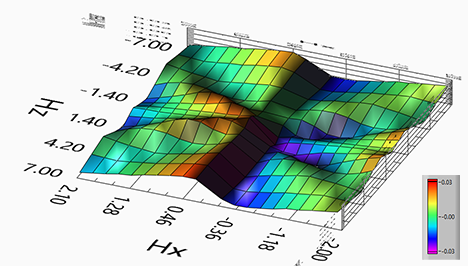
The strength of the spin-orbit interaction exhibits oscillations as the external magnetic field increases. The oscillation is due to a periodic dependence of spin- orbit interaction on the magnetic field.

The oscillations of the strength of spin- orbit interaction are very clear in experimental measurements and are observed for any nanomagnet, which I have measured.

Oscillations of the strength of spin- orbit interaction
Nanomagnet with a single ferromagnetic layer   Nanomagnet with a single ferromagnetic layer   Slope is small and negative and, therefore, kSO is negative and small. Measured data (blue line) are oscillating on top of linear dependence. (red line)   Slope is large and positive and, therefore, kSO is positive and large.
(oscillations): There are clear oscillations on top of the linear dependence. The oscillation is due to a periodic dependence of spin- orbit interaction on the magnetic field. The oscillation is a feature of an interface and is stronger when interface contribution is larger and the bulk contribution is weaker
click on image to enlarge it

(How to measure?)

Measured dependence of anisotropy field H_ani vs. external magnetic field H_z has two components: (component 1): linear increase; (component 2) oscillating component

Two components of dependence H_ani vs. H_z

(component 1 of H_ani vs H_z) (general (main) dependency): linear dependency

The strength of spin-orbit interaction is linearly proportional to the external magnetic field H_z. As a result, the anisotropy field H_ani can be expressed as

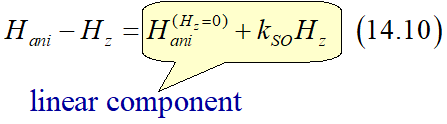
where H_z are external magnetic field, H_ani (H_z =0) is the anisotropy field in absence of the external magnetic field and k_SO is the coefficient of spin- orbit interaction.

(component 2 of H_ani vs H_z) (minor dependency): oscillating dependency

The strength of the spin-orbit interaction exhibits oscillations as the external magnetic field increases. These oscillations serve as a minor contribution to the primary linear dependence of H_ani vs. H_z, which slope is determined by the strength of the spin-orbit interactions.

where A_osc is amplitude of oscillation, H_period is the period of oscillations (the magnetic field, after which the oscillations repeats itself), H_phase is the phase of oscillations, H_decay is field for the decay of oscillations.

In total, the measured dependence Hani vs. Hz is fitted by formula:

(fact) This formula give a a perfect fitting of measured data for all nanomagnets I have measured so far.

The observed oscillations correspond to variations in the strength of the spin-orbit interaction as the external magnetic field increases.

There are clear oscillations on top of the linear dependence. The oscillation is due to a periodic dependence of spin- orbit interaction on the magnetic field. The oscillation is a feature of an interface and is stronger when interface contribution is larger and the bulk contribution is weaker

(interfacial origin of oscillations): The oscillations are weaker for a thicker nanomagnet, where the bulk contribution dominates, and stronger for a thinner nanomagnet, in which the interfacial contribution dominates. It clearly indicates the interfacial origin of the oscillations.

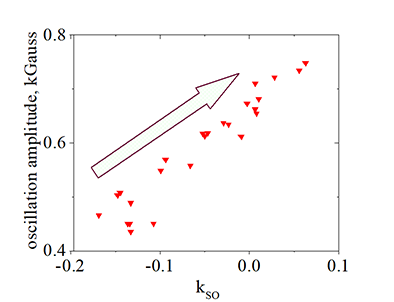
(linear proportionality of oscillation amplitude to the strength of spin- orbit interaction): The measured amplitude A_osc of oscillation is linear proportional to the strength of the spin-orbit interaction or , the same, to the coefficient of SO (kso). It is true for nanomagnets fabricated on a single wafer (See Fig.19) and for the nanomagnets of a different size, material, composition, thickness, structure fabricated on different wafer (See Figs. 22b,22c below). The slope of dependence A_osc vs. k_SO is positive. Since the positive contribution to k_SO is from the interface, the positive means again the interfacial origin of the oscillations.

Distribution of oscillation amplitude vs. strength of spin orbit interaction	Raw data
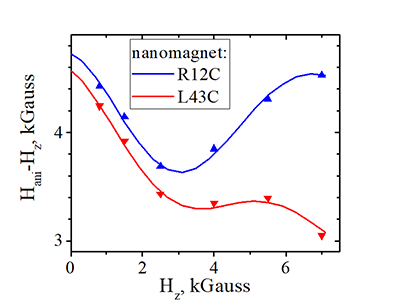Fig. 19 Measured amplitude of oscillation of the strength of spin- orbit interaction vs. measured coefficient kso of spin-orbit interaction. Each dot corresponds to a measurement of one individual nanomagnet fabricated at a different place of one wafer. The variations of amplitude and kso are due to variations of roughness and thickness over the wafer. Arrow shows the tendency.	Fig.19a. Measured anisotropy field Hani vs. external magnetic field Hz for two nanomagnets (R12C & L43C) fabricated on the same wafer Volt57B. Dots are measured data, lines are fitting. The fitting is perfect in both cases. Nanomagnet R12C has a stronger spin-orbit (kso= + 0.06) and a larger oscillation amplitude of 0.75 kG. Nanomagnet L43C has a weaker spin-orbit (kso= - 0.17)(slope is negative) and a smaller oscillation amplitude of 0.46 kG.
The dependence is clearly linear and the slope is positive!!	There is a clear correspondence between slope and oscillation amplitude!!!
wafer Volt57B :Ta(5 nm)/ FeCoB( x=0.5 1.1 nm) (click here fore more details)	click on image to enlarge it

(period of oscillation): The period H_period of oscillation is nearly identical for all nanomagnets and equals approximately 8 kGauss (See Fig. 21c below).

(note) When amplitude of oscillation becomes, there is some ambiguities of oscillation fitting. This is the reason why some nanomagnets show the period smaller than 8 kGauss

(phase of oscillations): The non-zero measured phase H_phase of oscillation means that the 1st maximum of oscillation is not at Hz=0, but is slightly shifted. For all measured nanomagnets, the phase H_phase is in range 0.1-0.2 kGauss.

(note) As 2023.06, I have not analyzed systematically the measured data of H_phase or its dependence or correlation with other measured parameters. The data of measured H_phase can be found in this origin file: AllSampleHani.opj

(decay of oscillations): The amplitude of oscillation decreases when the external magnetic field increases. Typically, at a half period of oscillation the oscillation amplitude decreases for about 40%. Some nanomagnets do not show any decrease of the oscillation amplitude and some nanomagnets show even an increase of the oscillation amplitude. The decrease or increase of the oscillation amplitude substantially depends on size, material, composition, thickness, and structure of the nanomagnet.

(note) The usage of the decrease or increase of the oscillation amplitude substantially improves the fitting of the experimental data. In this case, the fit data and the measured data are nearly undistinguished.

(note) As 2023.06, I have not analyzed systematically the measured data of H_decay or its dependence or correlation with other measured parameters. The data of measured oscillation amplitude at H_z=0 and at H_z= H_period/2 can be found in this origin file: AllSampleHani.opj

The data of measured H_ani, k_SO , H_period, , H_phase, H_decay for all nanomagnets, which I have measured so far, can be found in this origin file: AllSampleHani.opj

(systematic error due to oscillations): The amplitude of oscillation in a nanomagnet with a strong spin- orbit interaction (kso>0.2) becomes very large of about 1 kGauss and larger. It creates ambiguity of the fitting of the experimental data. The oscillating contribution may become dominating and there may be an ambiguity to distinguish the linear contribution. This can create some systematic error in measurement of k_SO and H_ani. See, for example, Fig. 19a above.

(fact) The oscillations of the strength of the spin- orbit interaction are large!!!

Especially, the oscillations are large in nanomagnets with a strong interfacial anisotropy and with a large spin-orbit interaction

Systematic measurements in FeCoB nanomagnets
Comparison of data of many different nanomagnets of a different size, material, composition, thickness, structure.
amplitude of oscillations vs. kso (full scale)   amplitude of oscillations vs. kso (small scale)   period of oscillations vs. kso   Samples. Thickness in nm shown in blankets       Fig.22b The amplitude of oscillations linearly depends on the strength of the spin- orbit interaction for both the single- layer and multi-layer nanomagnets. The linear dependence indicates the interfacial origin of the oscillations.   Fig.22c It is same figure as the left figure (Fig.22b) but in a different scale. For all single- layer nanomagnets, the dependence is linear with the same positive slope.   Fig.21c. The period is about 8 kGauss   The nanomagnet of a different width and length in range from 50 x 50 nm to 3000 nm x 3000 nm are shown.
Dots of the same color and shape correspond to nanomagnet fabricated at different places of the same wafer. Stars show multilayer nanomagnets, which contain several ferromagnetic layers.
click on image to enlarge it

Strength of spin- orbit interaction vs. interface roughness.

Strength of spin- orbit interaction vs. nanomagnet thickness.

There are small variations of thickness and interface roughness from a point to a point at the same wafer. Parameters of nanomagnets, which are fabricated at different places( e.g. at center or at edge of wafer or just at two close neighbor points), vary due to a variation of the interface roughness and due to a variation of the nanomagnet thickness.

The strength of spin orbit interaction and the demagnetization field are two parameters, which are directly affected by variations of thickness and roughness. Because of the variations of these two parameters, the anisotropy field H_ani and the intrinsic magnetic field are affected by variations of thickness and roughness as well.

(effect of interface roughness):

(k_SO & H_demag): A rougher interface reduces both the strength of the spin- orbit interaction k_SO and the demagnetization field H_demag.

(anisotropy field H_ani): A rougher interface may either decrease or increase the anisotropy field.

When the contribution of k_SO to H_ani dominates, a rougher interface causes a decrease of H_ani. H_ani is flowing the change of k_SO. E.g. it is a case of a single- layer nanomagnet.

When the contribution of H_demag to H_ani dominates, a rougher interface causes an increase of H_ani. H_ani is flowing the change of H_demag. E.g. it is a case of a multi- layer nanomagnet.

(intrinsic magnetic field H_int): H_int is affected strongly by the roughness. The internal magnetic field H_int is just a difference between the magnetic field along magnetization and the demagnetization field. For an ideally- flat surface (a non-existed subject), the demagnetization field exactly equal to the magnetization and, therefore, the becomes zero. A rougher interface reduces the demagnetization field and, therefore, increases the internal magnetic filed.

(effect of nanomagnet thickness):

(SO strength k_SO): There are different contributions to the total strength of SO from the bulk and the interface. As a nanomagnet become thinner .

(anisotropy field H_ani): A rougher interface may either decrease or increase the anisotropy field.

(intrinsic magnetic field H_int): H_int is not affected strongly by the nanomagnet thickness when the interface roughness and other parameters remains the same.

(Why there is a thickness variation): In MRAM applications, the FeCoB nanomagnet typically has a thickness of 1 nm. Considering that the interatomic distance in FeCoB is approximately 0.1 nm, this implies that there are merely around 10-15 atomic layers spanning the thickness. Consequently, the absence of even a single atom can lead to a significant variation of 5-10% in the thickness of the nanomagnet.

Distribution of the strength of spin-orbit interaction, anisotropy field and intrinsic magnetic field due to variations of thickness and roughness over one wafer.

Distribution of strength of spin- orbit interaction kSO and anisotropy field Hani due to variations of thickness and roughness is not random, but linear.
fact for nanomagnets fabricated at different places of one wafer
click on image to enlarge it

Two independent parameters, which are affect by variations of the nanomagnet thickness and the interface roughness: strength of spin-orbit interaction and demagnetization field.

(fact for nanomagnets fabricated at different places of one wafer) Distribution of strength of spin- orbit interaction k_SO, anisotropy field H_ani, intrinsic magnetic field and demagnetization field due to variations of thickness and roughness is not random, but linear.

(reason why:)Tendencies of how the strength of spin- orbit interaction and the demagnetization field are similar. A rougher interface makes the spin- orbit interaction weaker and the demagnetization field smaller. In a thicker nanomagnet, the bulk contribution is larger and, as consequence, the average spin- orbit interaction becomes smaller. The demagnetization field is not affected by a variation of the nanomagnet thickness.

(fact about distribution of H_ani and k_SO due to roughness/ thickness variation) The slope of distribution of H_ani vs. k_SO can be either positive (more common) or negative (less common). The slope is negative when the dogmatization field is larger and when the contribution due to the variation of the demagnetization field is dominated.

(slope polarity for distribution of H_int vs. k_SO) The slope is positive for single- layer nanomagnets which have a small coefficient k_SO of spin- orbit interaction and large internal magnetic field Hint. The slope is negative for multi- layer nanomagnets , which have a large k_SO and small Hint.

(slope polarity for distribution of H_int vs. k_SO) The slope is always negative for distribution of the internal magnetic field H_int vs. k_SO for both single- layer and multi- layer nanomagnets. (See Fig.44 above). It means that a smother interface always results in a larger coefficient k_SO of spin- orbit interaction and a smaller the internal magnetic field H_int. The Hint is smaller because the demagnetization field becomes larger for a smoother interface.

Measured anisotropy field vs. measured strength of spin-orbit interaction. Systematic study.
Comparison of data of many different nanomagnets of a different size, material, composition, thickness, structure.
Full scale Small scale Samples. Thickness in nm shown in blankets Measured anisotropy field vs. measured coefficient of spin-orbit interaction for nanomagnets of a different size, composition, structure. Arrows show the tendency for single-layer nanomagnets (blue arrow) and multi-layer- nanomagnets (brown arrow) It is the same graph as the left one, but in a different scale Dots of the same color and shape correspond to nanomagnet fabricated at different places of the same wafer. Stars show multilayer nanomagnets, which contain several ferromagnetic layers. The slope is positive for single- layer nanomagnets having a small kSO. The slope is negative for multi- layer nanomagnets (shown by stars) having a large kSO.   The nanomagnet of a different width and length in range from 50 x 50 nm to 3000 nm x 3000 nm are shown.
click on image to enlarge it

Why is the distribution of H_ani and k_SO measured for nanomagnets fabricated on one wafer important?

It is because in one wafer there are not so many variations of parameters. There is only a weak variation of interface roughness and a weak variation of the nanomagnet thickness. Other parameters remain the same. Therefore, it is easier to trace the effect of the roughness and thickness variations on parameters of a nanomagnet.

Different slope polarities in distribution of H_ani vs. k_SO in a single-layer and a multi-layer nanomagnet.

A single-layer nanomagnet means that there is only one ferromagnetic layer. For example, the FeB is only one ferromagnetic layer in the Ta:FeB:MgO nanomagnet. A multi-layer nanomagnet means that there are several ferromagnetic layers (e.g. Ta:FeB:W:FeB:W:FeB:MgO). Since the spin- orbit interaction is strongest at an interface, the number of interfaces affects greatly the magnetic properties of a nanomagnet

.

slope of Hani vs kSO. Single-layer vs. multi-layer nanomagnets.
single- layer nanomagnet vs. multi- layer nanomagnet multi-layer nanomagnets with different number of layers Anisotropy field Hani vs. coefficient kSO of SO interaction. Comparison of a single- ferromagnetic -layer and a multilayer- ferromagnetic -layer nanomagnet. Anisotropy field Hani vs. coefficient kSO of SO interaction for a multilayer- ferromagnetic -layer nanomagnet. Dependence on number of layers. The slope is positive for a single- ferromagnetic- layer nanomagnet. The slope is negative for a multi- ferromagnetic- layer nanomagnet. When number of layer is small (3 layer) the slope is still positive, but it becomes negative and its absolute value increases, when the number of ferromagnetic layers increases. However, when the number of layers reaches some critical value (6 layers in this case), the absolute value of the slope starts decreasing. single-layer nanomagnets: 53B Ta(2.5)FeBCo0.3(1); 55 Ta(5)FeB(0.9); 57ATa(5)FeBCo0.5(1.1); multi-layer nanomagnets: 45B W(3):[FeB(0.55) W(0.5)]5 FeB(0.55); 48A W(3): [FeB(0.45)/W(0.2)]7 FeB(0.45) (3 layers) 44B Ta(2):FeB(0.8):W(0.5):FeB(0.8):W(0.8):FeB(0.8); (5 layers) 46B W(3):[FeB(0.68)/W(0.25)]x4/ FeB(0.68); (6 layers) 45B W(3):[FeB(0.55) W(0.5)]5 FeB(0.55); (8 layers) 48A W(3): [FeB(0.45)/W(0.2)]7 FeB(0.45)
click on image to enlarge it

( vs. ) Why is the slope of dependence H_ani vs. k_SO positive for a single- ferromagnetic- layer nanomagnet, but negative for a a multi- ferromagnetic- layer nanomagnet?

Both the demagnetization field H_demag and the magnetic field H_SO of spin- orbit interaction are originated at an interface and, therefore, become larger when the number of interfaces increases. In a multilayer nanomagnet, the number of interfaces is larger. For this reason, both k_SO and H_demag are larger in a multilayer nanomagnet

The internal magnetic field H_int is smaller when H_demag is larger. For a smoother interface, k_SO becomes larger but Hint becomes smaller. Therefore, a positive change Δk_SO corresponds to a negative change ΔH_int.

H_int is small and k_SO is large in a multilayer nanomagnet. As a result, ΔH_int contribution to ΔH_ani is large, Δk_SO contribution is small and the slope is negative (See Eq. 42.3)

H_int is large and k_SO is small in a single- layer nanomagnet. As a result, ΔH_int contribution to ΔH_ani is small, Δk_SO contribution is large and the slope is positive (See Eq. 42.3)

( vs. vs. ) Why is the absolute value of slope of dependence H_ani vs. k_SO increases at first, when number of layers increases, but starts to decreases when the number of layer exceeds some critical number?

When the number of ferromagnetic layers increases, the interface roughness often increases as well. As a consequence, an increase of k_SO and H_demag due to the increase of the number of interface is overturned by the decrease of k_SO and H_demag due to the increase of the interface roughness.

Effect of increase of nanomagnet thickness or interface roughness on strength of spin-orbit interaction (kSO), demagnetization field (Hdemag) , anisotropy field (Hani) and internal magnetic field (Hint)
increase of interface roughness   increase of nanomagnet thickness   A rougher surface makes the strength of spin- orbit interaction weaker and the demagnetization field smaller. The internal magnetic field is a difference between magnetic field M along magnetization and demagnetization field. As the demagnetization decreases and, therefore, becomes more different from M, the internal magnetic field increases. The anisotropy field is linearly proportional to kSO and Hint. Therefore, Hani decreases due to the decrease of kSO, but increases due to the increase of Hint.   In a thicker nanomagnet, the negative bulk contribution to the strength of spin- orbit interaction becomes larger and the positive interface contribution becomes smaller. As a result, kSO decreases. The demagnetization field originates at the interface and is affected by the nanomagnet thickness. The anisotropy field is linearly proportional to kSO and , therefore, decreases with the decrease of kso.
click on image to enlarge it

Perfection of fabrication technology

Perfection of fabrication technology
(good fabrication technology: wafer 54A): all data points cluster tightly within a small circle with a small radius.     (bad fabrication technology: wafer 55): the measured data points are noticeably sparse, dispersed over a larger area.
click on image to enlarge it

In any technological application, it is crucial to ensure uniformity among the parameters of all devices fabricated on a single wafer. This holds particularly true for nanomagnets employed in memory or sensor applications, where consistency in magnetic parameters is of utmost importance. Among these parameters, the anisotropy field and the strength of the spin-orbit interaction stand out as key factors. By measuring the distribution of the anisotropy field against the coefficient of the spin-orbit interaction, one can obtain a clear indication of the quality and precision of the underlying technology being utilized.

The measured distribution of the anisotropy field (H_ani) against the coefficient (k_SO) of the spin-orbit interaction serves as an indicator of the fabrication technology's quality and precision:

(perfect fabrication technology): all data points cluster tightly within a small circle with a minimal radius.

(moderate fabrication technology): although there may be some slight scattering of data points, they still align along a straight line.

(bad fabrication technology): the measured data points are noticeably sparse, dispersed over a larger area.

Evaluation of a nanomagnet fabrication technology.
A measured distribution of Hani vs. kso is a good evaluation of the fabrication technology. The case, when all data points cluster tightly within a small circle with a minimal radius, is a clear indication of perfection of the fabrication technology.

How can I determine whether the variation in roughness or the variation in thickness is responsible for the changes in magnetic properties observed in nanomagnets fabricated on a single wafer?

The demagnetization field does not depend on the nanomagnet thickness. As a consequence, a variation of thickness does not affect the internal magnetic field H_int, but does affect the strength of spin-orbit interaction. The distribution H_int vs. k_SO along a straight horizontal line is a good indication that the variation of thickness is minimal.

It should be noted that the slope of distribution H_int vs. k_SO is increases for a smaller H_int and larger k_SO (See Fig 44 above)

Is the distribution of the coercive field H_c for nanomagnets fabricated on the same wafer related to the distribution H_ani vs. k_SO?

Yes. The coercive field H_c is related to H_ani and k_SO. A sparse distribution of H_ani vs. k_SO usually corresponds to a sparse distribution of H_c. However, there is one parameter, which may make the H_c distribution even more sparse. It is the size of the nucleation domain (see here).

The size of the nucleation domain depends very much on the smoothness, perfections and sharpness of the nanomagnet boundary, which may be very different from a nanomagnet to nanomagnet. As a consequence, a variation of size of the nucleation domain may be substantial even in the case of a reasonably good nanofabrication technology.

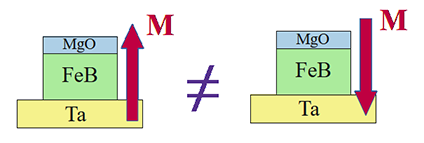
Dependence of strength of spin- orbit interaction on polarity of magnetic field

Dependence of strength of spin- orbit interaction on polarity of magnetic field
symmetrical nanomagnet   asymmetrical nanomagnet   In a symmetrical nanomagnet, the strength of spin- orbit interaction and the anisotropy field are the same for opposite magnetization directions.   In a asymmetrical nanomagnet, the strength of spin- orbit interaction and the anisotropy field are deferent for opposite magnetization directions. magnetization up = magnetization down   magnetization up ≠ magnetization down magnetization up: Ta/FeB+ FeB/Ta   magnetization up: Ta/FeB+ FeB/MgO magnetization down: FeB/Ta + Ta/FeB   magnetization down: FeB/Ta + MgO/FeB
click on image to enlarge it

There are two stable opposite magnetization directions along the nanomagnet easy axis. Both the strength of the spin- orbit interaction and the anisotropy field are different for those opposite magnetization directions.

The reason for the observed disparity is the correlation between the strength of the spin-orbit interaction and the orientation of the magnetic field relative to the orbital deformation taking place at the interface.

(demagnetization field vs. spin- orbit interaction): The demagnetization field remains unaffected by the magnetization polarity as it is solely a geometric phenomenon independent of polarity. On the other hand, the strength of the spin-orbit interaction does depend on magnetization polarity due to its reliance on the polarity of the orbital deformation with respect to the interface. Specifically, it is influenced by the direction of the orbital center's shift in relation to the nuclear position. The strength of the spin-orbit interaction varies depending on whether the magnetic field is applied in the same direction as the shift or in the opposite direction.

(how to measure) There is a substantial difference in measured dependence of anisotropy field vs. an external magnetic field H_z, which is applied along the easy axis, for two opposite directions of H_z. Both the offset of the dependence (H_ani) and the slope (k_SO) are different for opposite directions of the magnetic field.

Measured dependences of Hani and kSO on polarity of magnetic field & magnetization
There is a difference of offset (Hani) and slope (kSO) of the lines between measurements when the magnetization direction is up (shown in blue) and the magnetization is down (shown in red) The same graph as shown in the left, but versus absolute value of Hz. It allows to compare the difference for opposite direction of the magnetic field Measurement of 0 deg corresponds to a scan of in-plane magnetic field along current. Measurement of 90 deg corresponds to a scan of in-plane magnetic field perpendicularly to the electrical current. Independent measurements give the same difference of the offset (Hani) and slope (kSO)
Anisotropy field Hani vs. external magnetic field. Dots are measured data. Lines are fit.
wafer VOLT 58A Ta(5 nm)/ (FeCoB 1 nm, x=0.3) (see here) nanomagnet L43C SOT
click on image to enlarge it

(fact): The variation in the strength of the spin-orbit interaction in relation to magnetization reversal is a characteristic commonly found in nearly all interfaces.

What is the reason behind the lack of variation in the strength of the spin-orbit interaction during magnetization reversal for a symmetrical nanomagnet?

For a symmetrical nanomagnet, the absence of variation in the strength of the spin-orbit interaction with respect to magnetization reversal can be attributed to its balanced and uniform structure. There are two equal but opposite interfaces in a symmetrical nanomagnet. For example, in Ta/FeB/Ta nanomagnet there are two opposite interfaces: Ta/FeB and FeB\Ta. A variation in the strength of spin- orbit is the same, but opposite at each interface. In total, there is no variation for the symmetrical nanomagnet.

When the magnetization direction is up, the magnetic field penetrates from Ta to Fe at the lower interface and from Fe to Ta at the upper interface. When the magnetic field is reversed, there is still one interface (the upper one), where the magnetic field penetrates from Ta to Fe, there is one interface (the lower one), where the magnetic field penetrates from Fe to Ta. Even though the strength of the spin-orbit interaction is different between cases when the magnetic field penetrates from Ta to Fe and from Fe to Ta, there is no difference for the whole nanomagnet.

Symmetrical vs. Asymmetrical nanomagnets
Symmetrical Symmetrical Asymmetrical wafer VOLT 58A Ta(5 nm)/ (FeCoB 1 nm, x=0.3) (see here) nanomagnet L43C SOT wafer Volt 59A Ta(8 nm)/ FeB(0.9 nm) (see here) nanomagnet L75C SOT wafer Volt 46B W(3):[FeB(0.68)/W(0.25)]x4/ FeB(0.68) nanomagnet free18.
Anisotropy field Hani vs. external magnetic field. Dots are measured data. Lines are fit.
wafer VOLT 58A Ta(5 nm)/ (FeCoB 1 nm, x=0.3) (see here) nanomagnet L43C SOT
click on image to enlarge it

Origin for dependence of the strength of spin-orbit interaction on the polarity of magnetization

Why does the strength of the spin- orbit interaction depend on the magnetization polarity?

(reason why the strength of the spin-orbit interaction increases under an external magnetic field):

The increase in the strength of the spin-orbit interaction with an increase in the external magnetic field can be attributed to the difference of orbital modifications under the influence of the Lorentz force.

The part of the orbital that rotates clockwise around the magnetic field contracts due to the Lorentz force, bringing it closer to the nucleus, where the electric field is stronger. Consequently, this portion of the orbital experiences a greater spin-orbit magnetic field.

Conversely, the counterclockwise rotating portion of the orbital expands and moves away from the nucleus, resulting in a smaller spin-orbit magnetic field.

Since the electric field diminishes with increasing distance from the nucleus following a 1/r decay, the gain from the clockwise rotating component surpasses the loss from the counterclockwise rotating component. As a result, the electron experiences an overall amplified magnetic field due to the spin-orbit interaction.

(reason why the the strength of the spin-orbit interaction depends on the polarity of an external magnetic field):

When the magnetic field is reversed, the clockwise component expands and the counterclockwise component contracts. However, due to the asymmetric nature of the orbital at the interface, the gain and loss of the spin-orbit interaction differ from the previous case. Consequently, the total gain in the magnetic field from the spin-orbit interaction varies for opposite polarities of the external magnetic field.

(orbital quenching) Given that the orbital moment of localized electrons is completely quenched (see here) , resulting in a net orbital moment of zero, it raises the question of why an asymmetry exists between the clockwise and counterclockwise components of the orbital. Furthermore, what causes the interaction between the clockwise component and the up-magnetic field to differ from the interaction between the counterclockwise component and the down-magnetic field?

Indeed, you are correct. The orbital moment of localized electrons is effectively quenched, resulting in no net orbital moment. This is achieved by the compensating contributions from the orbital components associated with electrons rotating in clockwise and counterclockwise directions. However, it is important to note that this compensation occurs for the overall orbital as a whole.

On a local scale, there can still be subtle differences. For instance, the clockwise component may be slightly shifted to the left, while the counterclockwise component may be shifted to the right due to variations in the surrounding atoms on the left and right sides of the orbital. As a result, there can be localized differences in the interaction of the clockwise and counterclockwise rotating components with an external magnetic field.

(bulk vs. interface) What is the underlying reason for the significant dependence of the strength of the spin-orbit interaction on the magnetization polarity specifically at the interface, while such dependence is absent in the bulk of a ferromagnet?

For the spin-orbit interaction to exhibit a dependence on magnetization polarity, a distinct spatial symmetry of the electron orbital must be disrupted. Typically, this symmetry is broken at the interface but remains intact in the bulk of a ferromagnetic material. While local symmetry breaking can occur, on average, the symmetry is maintained within the bulk.

The bulk of the ferromagnetic material resembles a multilayer nanomagnet, where each interface breaks the symmetry, but subsequent interfaces exhibit equal and opposite symmetry breaking. As a result, the overall symmetry remains unbroken.

(neighboring orbitals) Does the contraction or expansion of an electron's orbital under the influence of the Lorentz force take into account the neighboring orbitals of other localized electrons surrounding it?

Indeed, the orbital of a localized electron forms strong bonds with the orbitals of neighboring atoms. Because of the strong bonding, the strength of these bonds remains unaltered under the influence of an external magnetic field. However, within the context of unchanged overall bonding strength, there is a redistribution of the clockwise and counterclockwise rotation components of the orbital, which helps to break the required spatial symmetry.

The presence of neighboring orbitals plays a significant role in breaking the required spatial symmetry. For instance, when different atoms are situated on each side of the orbital, the center of the orbital becomes shifted away from the nucleus position. Furthermore, such neighboring orbitals make the clockwise and counterclockwise rotation components of the orbital experience shifts in different directions, thereby breaking the symmetry between them. As a result, the interaction of the clockwise and counterclockwise rotating components with an external magnetic field becomes different.

Distribution of a change of Hani vs. a change of kso under magnetization reversal

The anisotropy field (H_ani) and the coefficient of spin-orbit interaction (k_SO) both exhibit a dependence on the magnetization polarity. These dependencies are not independent but are correlated with each other. Specifically, a larger change in k_SO corresponds to a smaller change in H_ani when the magnetization is reversed.

Change of anisotropy field and strength of spin- orbit interaction under magnetization reversal.
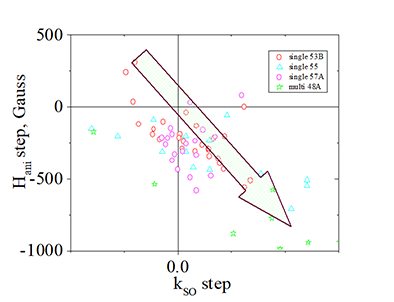Each dots corresponds to a measurement of one nanomagnet. Dots of the same shape and color correspond to nanomagnets fabricated on the same wafer.
A negative slope is very clear. A nanomagnet, which have a larger step of kso, has a smaller step of Hani.
click on image to enlarge it

What is the explanation for the negative slope observed in the distribution of the change in anisotropy field versus the change in the strength of the spin-orbit interaction under a reversal of magnetization?
The distinction in the strength of the spin-orbit interaction during magnetization reversal is evident, but it is expected that the demagnetization field remains unaffected as it is purely a geometrical phenomenon. Consequently, one would anticipate a positive slope in the distribution. However, experimental observations reveal a negative slope. The question then arises: why is this the case?
As 2023.06, the reason for the experimentally- observed negative slope of distribution ΔHani vs. ΔkSO is not understood.

This correlation becomes evident when comparing measurement data from nanomagnets fabricated on the same wafer. Within a single wafer, there are slight variations in thickness and interface roughness from point to point. Consequently, nanomagnets fabricated at different locations, such as the center or edge of the wafer, or even neighboring points, will exhibit variations in their parameters due to differences in interface roughness and nanomagnet thickness.

(fact) The strength of spin-orbit interaction and, therefore, k_SO does depend on the magnetization polarity

It is because the position of the center of the electron orbital with respect to the nucleus position is shifted towards (outwards) the interface. The magnetic field opposite or along that shift induces a different strength of spin- orbit interaction.

(fact) The demagnetization field does not depend on the magnetization polarity

It is The demagnetization is a geometrical effect. There is any reason why the demagnetization filed should depend on the magnetization polarity.

(unexplained experimental fact): negative slope between a change of k_SO vs change of H_ani under magnetization reversal

H_ani is proportional to k_SO and the internal magnetic field H_int:

Since the demagnetization field remains unaffected by changes in magnetization polarity, the internal magnetic field Hint: should be independent of the magnetization polarity as well. Therefore, one would expect the change in anisotropy field with magnetization reversal to have the same polarity as the change in kso. However, contrary to these expectations, the observed polarity in experiments is opposite.

(A possible reason): dependence of demagnetization field on the magnetization polarity

But why and how? What is the mechanism?

The negative slope is a systematic feature, which is observed in all studied wafer

Change of anisotropy field and strength of spin- orbit interaction under magnetization reversal. Systematic study.
Comparison of data of many different nanomagnets of a different size, material, composition, thickness, structure.
Full scale small scale Samples. Thickness in nm shown in blankets Measured step of anisotropy field vs. measured step of coefficient of spin-orbit interaction as magnetization is reversed to opposite direction measured for nanomagnets of a different size, composition, structure. Arrows show the tendency. It is the same graph as the left one, but in a different scale Dots of the same color and shape correspond to nanomagnet fabricated at different places of the same wafer. Stars show multilayer nanomagnets, which contain several ferromagnetic layers. The slope is negative for both single-layer and multi- layer nanomagnets.   The nanomagnet of a different width and length in range from 50 x 50 nm to 3000 nm x 3000 nm are shown.
click on image to enlarge it

Examples. Measured dependences of H_ani and k_SO on polarity of magnetic field & magnetization

Measured dependences of Hani and kSO on polarity of magnetic field & magnetization
large Hani~9 kG, kSO>0 small Hani~3 kG, kSO<0 moderate Hani~7 kG , kSO<0 wafer Volt48A nanomagnet L74C g wafer Volt54A nanomagnet R65C wafer VOLT 58A Ta(5 nm)/ (FeCoB 1 nm, x=0.3) (see here) nanomagnet L43C
Anisotropy field Hani vs. external magnetic field. Dots are measured data. Lines are fit.
Measurement of 0 deg corresponds to a scan of in-plane magnetic field along current. Measurement of 90 deg corresponds to a scan of in-plane magnetic field perpendicularly to the electrical current. Independent measurements give the same difference of the offset (Hani) and slope (kSO)
(note) In all shown nanomagnets, the split due to magnetization reversal is identical for the 0-deg and 90-deg scans. It is not always the case.
click on image to enlarge it

Dependence of strength of spin- orbit interaction on direction of magnetic field

The strength of spin-orbit interaction relies on the relative angle between the magnetization and the magnetic easy axis or the surface normal for a nanomagnet with PMA. At particular angles, there exists a peak or a trough in the strength of the spin-orbit interaction. This specific angle corresponds to characteristics related to the distortion of electron orbitals resulting from bonding at the nanomagnet's interface. Across all nanomagnets examined, a consistent and systematic correlation was observed between the magnetization angle and the spin-orbit interaction.

Considering that the standard method for measuring the strength of spin-orbit interaction involves tilting the magnetization under an external magnetic field, how can one effectively determine the relationship between the spin-orbit interaction strength and the angle of magnetization tilt?

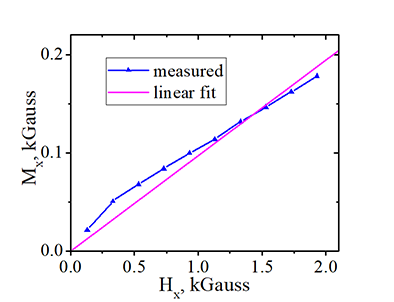
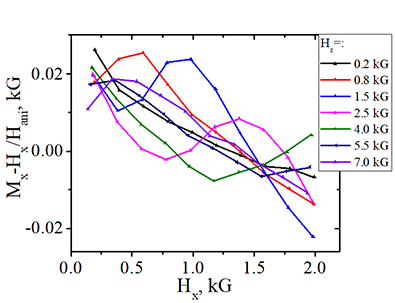
In addition to the prominent linear relationship between M_x and H_x, which serves as the basis for assessing the strength of spin-orbit interaction , there exists a secondary weak oscillatory dependence on the tilting angle. This weak oscillating pattern allows for the evaluation of the angle dependency of the spin-orbit interaction.

Major prominent linear relationship between M_x and H_x, from which the strength of the spin orbit interaction is evaluated,:

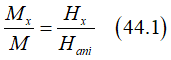
where M_x is in-plane component of the magnetization, H_x is in-plane external magnetic field and H_ani is the anisotropy field , which is evaluated from the linear fitting of measured data of M_x vs. H_x.

Real measured dependency between M_x and H_x,

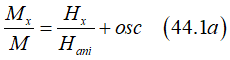
where osc is a very weak oscillations.

measured dependency Mx vs. Hx, & its linear fit	Deviation of measured Mx vs. Hx from linear Relationships Mx-Hx/Hani
		wafer Volt40A nanomagnet L43C

wafer Volt54A nanomagnet R65C	wafer Volt58A nanomagnet L23C	wafer Volt40A nanomagnet L43C

Dependence of strength of spin- orbit interaction on current and temperature. SOT effect.

Dependence of strength of spin- orbit interaction on gate voltage. VCMA effect.

more details about VCMA effect is here

 

 

voltage-controlled magnetic anisotropy. VCMA effect.

The VCMA effect describes the modulation of the magnetic properties of ferromagnetic metal by a gate voltage

Under a gate voltage, magnetic properties of ferromagnetic metal (Fe) are changed. For example, the magnetization direction changes. Gate voltage is not applied to bulk to Fe, but only to Fe/oxide. Still the gate voltage greatly affects magnetic properties of Fe

The gate voltage modulates the coercive field, anisotropy field, spin polarization, the absolute value of the magnetization and magnetization switching time

click on image to enlarge it

There is a screening of the gate voltage in the bulk of the nanomagnet. Even though the gate voltage is applied to the nanomagnet, in fact, due to the screening the gate voltage is only applied to the interface and, therefore, modulation of magnetic properties of the interface by the gate voltage is the key effect here.

Change of strength of spin- orbit interaction and anisotropy field under a gate voltage
Anisotropy field     Measured Hani vs perpendicular- to- plane external magnetic field Hz. Lines of different color correspond to a measurement under a different gate voltage. Measured anisotropy filed Hani and coefficient of spin- orbit interaction kSO as a function of the gate voltage. Measured change of anisotropy filed ΔHani and the coefficient of spin- orbit interaction ΔkSO as the gate voltage changes from 0 V to 1 V. Each dots corresponds to a measurement of a different nanomagnet fabricated at a different part of the same wafer. The dependence on the gate voltage is substantial. Both the offset (Hani) and the slope (kSO) of the line depend on the gate voltage. The dependencies are opposite. Hani is largest at a negative gate voltage. kSO is largest at a positive gate voltage. Even though the change is slightly different from a nanomagnet to a nanomagnet, ΔHani is always positive and ΔkSO is always negative Even in the absence of an external magnetic field the Hani depends on gate voltage. It decreases as the gate voltage increases. Additionally, the slope of lines depends on the gate voltage. Due to a different slope, the gap between lines decreases at a larger field.
wafer Volt 54a (see here), nanomagnet L25C
click on image to enlarge it

Possible reason why an increase of anisotropy field sometimes does lead to an increase of anisotropy field

The magnetic anisotropy itself is originated by the spin-orbit interaction. In absence of the spin- orbit interaction there is no magnetic anisotropy and the anisotropy field H_ani equals zero. It is plausible to assume that an increase of the strength of the spin- orbit interaction always leads to an increase of the anisotropy field. Often it is true. However, sometimes the dependency is opposite, an increase of the strength of the spin- orbit interaction is accompanied by an decrease of the anisotropy field, when some of nanomagnet parameters changes. It is because additionally there are changes of the demagnetization field and the internal magnetic field, which can be opposite to the change of the spin-orbit interaction and which can reverse the change of H_ani.

.

Sum of symptomatic measurement in many samples: download origin file:AllSampleHani.opj

Systematic measurements in FeCoB nanomagnets of a different structure and composition
dependence on anisotropy field Hani
strength of spin-orbit interaction kSO   amplitude of oscillations of strength of spin-orbit interaction vs external magnetic field   period of oscillations of strength of spin-orbit interaction vs external magnetic field   Samples. Thickness in nm shown in blankets       Fig.21a. Strength of spin-orbit interaction is largest in multilayer nanomagnets, which are shown by stars and which contain several ferromagnetic layers. There is a linear dependence between kSO vs. Hani. In case of a single- layer nanomagnet, the slope of the linear dependence is positive. In case of a multi- layer nanomagnet, the slope is negative.   Fig.21b. The dependency is sparse, because it is indirect.. In case of a single- layer nanomagnet, the slope is approximately positive. In case of a multi- layer nanomagnet, the slope is approximately negative. Oscillation amplitude depends directly on kSO (see graph below) and kSO depends on Hani (see left graph).   Fig.21c. The period is about 8 kGauss and becomes smaller for nanomagnets with small oscillation amplitude.
dependence on strength of spin-orbit interaction kSO
internal magnetic field, Hint   amplitude of oscillations of strength of spin-orbit interaction vs external magnetic field   amplitude of oscillations of strength of spin-orbit interaction vs external magnetic field   Samples. Thickness in nm shown in blankets       Fig.22a. It is the internal magnetic field, which holds the magnetization of the nanomagnet along its easy magnetic axis. The internal magnetic field is stronger for single- layer nanomagnets and weaker for multi-layer nanomagnets (shown by stars).   Fig.22b The amplitude of oscillations linearly depends on the strength of the spin- orbit interaction for both the single- layer and multi-layer nanomagnets. The linear dependence indicates the interfacial origin of the oscillations.   Fig.22c It is same figure as the left figure (Fig.22b) but in a different scale. For all single- layer nanomagnets, the dependence is linear with the same positive slope.
Dots of the same color and shape correspond to nanomagnet fabricated at different places of the same wafer. Stars show multilayer nanomagnets, which contain several ferromagnetic layers.
click on image to enlarge it

Strength of spin-orbit interaction is largest in multilayer nanomagnets, which are shown by stars and which contain several ferromagnetic layers. There is a linear dependence between k_SO vs. H_ani. In case of a single- layer nanomagnet, the slope of the linear dependence is positive. In case of a multi- layer nanomagnet, the slope is negative.

Questions about measurement of strength of spin- orbit interaction

(SO from bulk and interface) Is it possible to separately quantify the contributions to the strength of spin-orbit interaction from the bulk of the nanomagnet and from the interface?

A. (2024.03) Quantifying individual contributions to the strength of spin-orbit interaction from the bulk and the interface of the nanomagnet is a challenging task, albeit potentially feasible. The measured data (See Fig. above) presents a qualitative assessment, derived from the clear observation that the strength of spin-orbit interaction increases with the number of interfaces, along with the negative kso systematically measured for thick single-layer nanomagnets with predominant bulk contribution.

As demonstrated above (see here) , a negative value of kso indicates that while all elements of the tensor of spin-orbit interaction remain positive, the spin-orbit interaction is greater in the in-plane direction than in the perpendicular-to-plane direction.

The challenge of separating bulk and interface contributions arises from the significant influence of interface roughness on spin-orbit interaction, compounded by difficulties in maintaining uniformity of interface roughness across nanomagnets of varying thicknesses.

(orbital deformation at interface)Why do the orbitals of Fe and Co undergo significant deformation at an interface, and how does it influence the spin-orbit interaction?

A. (2024.03) The atomic environment surrounding Fe and Co atoms differs significantly at the interface compared to the bulk. In the bulk, Fe atoms are surrounded only by other Fe atoms, resulting in nearly isotropic spin-orbit interaction. However, at the interface, the surrounding atoms differ above and below the Fe atoms, leading to asymmetric forces experienced by the atom from different directions, which leads to an orbital deformation in comparison with a bulk Fe atom.

As depicted in Fig. (see above), the measured value of kso for single-layer nanomagnets with a larger bulk contribution is close to 0, indicating that the strength of spin-orbit interaction is nearly equal in all directions. In contrast, kso approaches a value of 9 for multilayer nanomagnets, where the interface contribution is predominant. This suggests that at the interface, where Fe atoms are subject to deformation, the spin-orbit interaction is significantly stronger in the perpendicular-to-plane direction than in the in-plane direction.

(SO under external magnetic field )It is not clear how the external magnetic field would induce the SOC. Indeed, the linearity of relation between Hso and Hext would imply that SOC breaks time-reversal symmetry, which is not true for "pure" SOC, but certainly for the external magnetic field.

A. (2024.03) Due to its relativistic nature, the spin-orbit interaction manifests itself only when the time-reversal symmetry (T-symmetry) of an electron orbital is broken. However, the spin-orbit interaction itself cannot break the T-symmetry—it necessitates an external T-symmetry-breaking factor. This only occurs when the electron is subjected to conditions where T-symmetry is already broken. There are a limited number of scenarios where this occurs: (1) in the presence of an electrical current, (2) when the electron possesses a nonzero orbital moment due to its non-quenched state, and (3) when an external magnetic field is applied. It's noteworthy that the intrinsic magnetic field within a ferromagnetic or antiferromagnetic material is regarded as an external field. Consequently, the necessity of a broken T-symmetry for the spin-orbit interaction's existence already clarifies why its strength is proportional to the external magnetic field.

While slightly oversimplified, the following provides a very illustrative explanation: Consider a fully quenched electron orbital under an external field. This scenario closely resembles the behavior of a localized d- electron in materials such as Fe or Co, which are nearly fully quenched, as indicated by FMR (Ferromagnetic Resonance). Full quenching implies that the orbital moment is zero, and the electron wavefunction can be divided into two components corresponding to clockwise and counterclockwise movements. In the absence of the orbital moment and external magnetic field, these two components experience equal but opposite magnetic fields of spin-orbit interaction due to the electrical field of the nucleus. Consequently, these contributions balance each other, resulting in the electron experiencing no net spin-orbit interaction. This is the case when T-symmetry is unbroken for the orbital movement. Reversing the flow direction of time implies an exchange between clockwise and counterclockwise movement paths, which, in this case, doesn't alter anything. For spin-orbit interaction to exist, there must be a distinction between clockwise and counterclockwise rotations, indicating the breaking of T-symmetry. This symmetry can be externally broken by applying a magnetic field, which creates the Lorentz force. The Lorentz force affects the electron differently along its clockwise and counterclockwise paths. The force pushes the clockwise-rotating part of the electron wavefunction away from the nucleus while drawing the counterclockwise-rotating part closer to it. This creates a disparity in the electric field of nucleus experienced by the electron for these two opposite rotations. As a result, the equilibrium between opposing magnetic fields of spin-orbit interaction is disrupted, leading to a significant magnetic field of spin- orbit interaction experienced by the electron.

(2024) (about linear relationship between SO and external field) You assumed a linear relationship between Hso and Hext was assumed: Hso = kso · Hext ,where kso is the coefficient of spin- orbit interaction. There is no theory or reference to support this assumption.

The linear relationship between the strength of the spin-orbit interaction and the external magnetic field is rooted in the relativistic nature of spin-orbit interaction and, importantly, in the fundamental features of broken time-reversal symmetry (T-symmetry). Due to its relativistic origin, the spin-orbit interaction occurs only when T-symmetry is externally broken. It's crucial to note that spin-orbit interaction cannot break T-symmetry by itself.

Depending on the source of the T-symmetry breaking, there are three distinct types of spin-orbit interaction. For the first type, T-symmetry is broken by an electrical current, as seen in phenomena like the Spin Hall effect. For the second type, occurring in unquenched electrons, T-symmetry is broken due to the orbital moment (e.g., alignment of spin and orbital moments in an atomic gas). For the third type, which is responsible for magnetic anisotropy, T-symmetry is broken by a magnetic field.

Since there is no spin-orbit interaction in the absence of a magnetic field H, and the polarity of Hso follows the polarity of H, Hso should be an odd function of H, meaning it should be proportional to the 1st, 3rd, 5th orders of H. Experimental evidence clearly indicates that the linear component is the largest, while other components are negligible, at least in the case of classical ferromagnetic metals like Fe and Co.

(other methods to measure SO) How does the measurement of the strength of spin-orbit interaction by your method compare to other measurement methods? For instance, by spin transport [Kawahala et. al. AIP Advances 10, 065232 (2020)], anisotropic spin-orbit interaction by in-plane magnetoresistance [R. Gunnarsson. PRB 85, 235409 (2012)], quasiparticle interference imaging [Sun et. al. Nat. Comm. vol. 14, 3771 (2023)], time-resolved charge detection [Hofmann et. al. Phys. Rev. Lett. 119, 176807 (2017)], theoretical proposal of anisotropic Kondo screening, as tool to measure the ratio of Rashba and Dresselhaus SOC strengths in the wire [Vernek et. al. Phys. Rev. B 102, 155114 (2020)],

A. (2024.03) The spin-orbit interaction exists only when the time-inverse symmetry (T-symmetry) is broken. There are three very different types of spin-orbit interaction, each corresponding to a distinct method of breaking T-symmetry. The features and properties of each type of spin-orbit interaction are drastically different, necessitating the assignment of a unique designation to each type to avoid possible confusion.

The interaction between the magnetic field of spin-orbit interaction and electron spins results in different energies for light-hole, heavy-hole, and split-off bands for valence electrons in a semiconductor. The second way to break T-symmetry is due to the flow of an electrical current. This type of spin-orbit interaction is responsible for the existence of the whole family of magneto-transport effects (the Spin Hall effect, AHE, AMR/PHE effect and so on). These effects arise from spin-dependent scatterings. The scatterings become spin- dependent because of spin-orbit interaction, resulting in the breaking of T-symmetry by the electrical current. The third way to break T-symmetry is by applying an external magnetic field. This type of spin-orbit interaction is responsible for magnetization alignment in a magnet and for magnetic anisotropy. Only the measurement of the last type of spin- orbit interaction is described above.

All references you mentioned pertain to magneto-transport effects, which are associated with the second type of spin-orbit interaction.

(2024) ( removing bulk contribution) You use the following plot Hanis-Hz=Haniz,0 -k z Hz. Why do not present simply Hanis=Haniz,0 -(k z-1) Hz? It is cleaner and, in my opinion do not introduce an artificial trend.

The term H_anis=H_z in the equation corresponds to the bulk contribution, representing the alignment of magnetization along the total magnetic field in vacuum, which doesn't provide informative insights. Consequently, when conducting data analysis, it is more advantageous to utilize the relationship between H_anis-H_z , and H_z. This approach ensures that the significant bulk contribution does not obscure a potentially weaker dependence on k_so.

Please see this figure here

(2024) (about edge domains) You simplified your analysis by ignoring possible edge-domain formation in your sample. Give experimental proof on the domain configurations of the sample.

The experiment is performed at a high magnetic field higher than 1 kGauss, at which magnetic domains do not exist. Additionally, nanomagnets are specifically utilized due to their lack of magnetic domains, simplifying data analysis. However, this measurement method allows for its application to larger samples without significant issues.

The presence and impact of magnetic domains under a weak magnetic field can be easily identified in this measurements, and their influence can be removed by a slight increase in the magnetic field.

(2024) (about positive and negative polarity of kso) The Kso for bilayer and multilayer are negative and positive, whether this phenomenon is universal or only correct for some special materials?

This trend is highly systematic. For all studied nanomagnets, kso consistently exhibits a large and positive value in multilayer nanomagnets. In contrast, for single-layer nanomagnets, kso is always small and can be either positive or negative.

A negative value of kso indicates that the strength of the spin-orbit interaction in the in-plane direction is greater than in the perpendicular-plane direction . Generally, the interface kso contribution is positive, while the bulk kso contribution is often negative.

In FeB and FeCoB amorphous nanomagnets, the major contribution to kso originates from interfaces, which is positive and accumulates with an increasing number of interfaces. This is why kso is large in multilayer nanomagnets. However, the strength of the spin-orbit interaction strongly depends on interface imperfections, such as roughness and sharpness. An increase in the number of interfaces leads to an increase in interface imperfections, which eventually causes a decrease in kso after a certain number of interfaces. Therefore, precise fabrication is key to achieving a large positive kso.

(2024) (about positive and negative polarity of kso 2) From your measurement data, I found the Kso varied from negative to positive FeB/Ta and FeCoB/Ta bilayer samples, whether this phenomenon is mainly related to the interface roughness or other factors? The experimental data looks a bit confusing.

(variation of kso between positive and negative values) The interface kso contribution is positive, while the bulk kso contribution is often negative. The sign of kso is determined by the balance between these contributions. In thicker nanomagnets, the bulk contribution predominates, resulting in a negative kso. Conversely, in thinner nanomagnets, the interface contribution is dominant, leading to a positive kso

(variation of kso for a different nanomagnets fabricated on the same wafer): A variation in kso was observed among the data points of nanomagnets fabricated at different locations on the same wafer. It was noted that the closer two nanomagnets are to each other, the smaller the differences in kso tend to be. A more homogeneous and smoother wafer corresponds to reduced kso variation. This spread in data serves as an indicator of the precision of the fabrication technology. Both variations in thickness and surface roughness contribute to data dispersion on a wafer. Given that nanomagnet thickness is around 1 nm, even a variance within the range of a single atomic layer can markedly impact kso. Moreover, it was experimentally observed in this work that the surface roughness and the surface sharpness play an even more substantial role, exerting a notable influence on kso.

(2024) (about the large measured value of kso) Moreover, the experimental value of kso=2.15 seems to be very big.

The large value of kso is common in multilayer nanomagnets. In FeB and FeCoB amorphous nanomagnets, the major contribution to kso originates from interfaces, and this contribution accumulates with an increasing number of interfaces. This is why kso is large in multilayer nanomagnets. However, the strength of the spin-orbit interaction strongly depends on interface imperfections, such as roughness and sharpness. An increase in the number of interfaces leads to an increase in interface imperfections, which eventually causes a decrease in kso after a certain number of interfaces. Therefore, precise fabrication is key to achieving a large kso.

My current fabrication technology is good and I am able to fabricate nanomagnets with a large kso, but I believe that using more advanced fabrication technologies could yield even higher values of kso.

(2024) (about possible error when the scanning field Hx is close to the anisotropy field Hani)) My concern is about the measure of the anisotropy field. Assuming a perpendicular anisotropy K, the energy reads E = µ0 ( -Hx Mx -Hz Mz) +(µ0M²/2-K) Mz²/M². Replacing Mz by sqrt(M² -Mx²) when Hz > 0, we obtain E = µ0 ( -Hx Mx -Hz sqrt(M² -Mx²) ) +(µ0M²/2-K) (M² -Mx²)/M² At equilibrium, ∂E/∂Mx = 0 thus µ0 (Hz Mx/sqrt(M² -Mx²) ) +(2K-µ0M²) Mx/M² = µ0 Hx This relation is approximated by µ0 (Hz Mx/M ) +(2K-µ0M²) Mx/M² = µ0 Hx. This approximation yields a linear relation between Mx and Hx. The anisotropy field is then defined as Hani = Hz + 2K/M -µ0M. Unfortunately, when Mx gets close to M, the approximation, which leads to the linear relation between Mx and Hx, is very bad.

I completely agree with you. When the scanning field is close to the anisotropy field, the approximation (Mx/M) ^2<<1 (Eq.A11 of AIP Advances (2024)) is no longer valid, and the relationship between Mx and Hx becomes non-linear. However, this limitation does not pose any issues in my measurements for the following reasons:

(reason 1) : Direct Calculation:

It is entirely feasible to calculate the anisotropy field Hani directly from the non-linear relationship between Mx and Hx without relying on any approximations, including Eq. A11 of AIP Advances (2024). Therefore, Hani can be evaluated from experimental data by a non-linear fitting without risking any error.

(reason 2) : Validity of Approximation:

For realistic parameters of FeCoB nanomagnets and the maximum magnetic field provided by my magneto-transport probe, the condition (Mx/M) ^2<<1 (Eq.A11) strictly holds for all the nanomagnets I have studied.

These factors ensure that the validity of the approximation does not introduce any complications in the interpretation or accuracy of the results.

(reason 1) (Calculation of explicit equation for relation between Hx and Mx):

The implicit non-linear relation between Mx and Hx was calculated in Appendix A of AIP Advances (2024) as

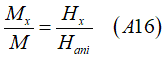
where

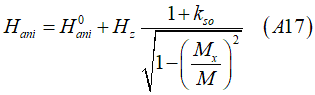
From Eq. (A17), the explicit non-linear equation for relation between Hx vs Mx is calculated as

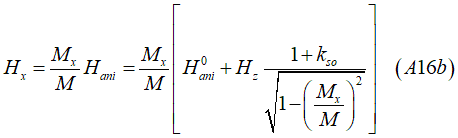
A non-linear fitting of the experimentally measured Mx vs.Hx data using Eq. A16b is employed to determine Hani. Prior to this, a linear fitting is performed to estimate an initial approximation of Hani and kso. These calculations are integrated into a program, which I specifically designed for analyzing the experimental data.

(reason 2) (Validity of Approximation (Mx/M) ^2<<1 (Eq.A11 of AIP Advances (2024)) for my samples + my probe limitations):

Although I have the option to perform a non-linear data analysis without relying on any approximations, I generally prefer linear data analysis. This preference arises because the difference between the results of the two methods is negligibly small, and linear analysis is more robust in the presence of additional oscillations in the data.

It is also worth noting that the maximum in-plane magnetic field generated by my probe is 2.2 kGauss, whereas the measured anisotropy fields of FeCoB nanomagnets under Hz are substantially larger, ranging from 5 to 30 kGauss. This ensures that the measurements are conducted well within the relevant field range for these nanomagnets.

Below graphs compare non- linear calculation (solid line, no approximations) with linear calculation (dot line) for most extreme possible  cases of measurements. You can see that in all cases the difference is negligible. A tiny difference appears only in the unrealistic case of a very small Hani=2.5 kGauss. It is worth notice that coercive field of a nanomagnet with  Hani=2.5 kGauss (Hz=0)  is extremely small (Hc<10 Gauss)  and which magnetization experiences the spontaneous  telegraphic switches

Correctness of linear approximation of relation Mx vs.Hx
dot line: linear approximation, solid line: no approximations
Mx: the component of magnetization perpendicular to the easy axis; Hx: magnetic field applied perpendicular to the easy axis

Questions about interface roughness

(interface roughness & SO )Why does interface roughness influence the strength of spin-orbit interaction?

A. (2024.03) As a result of interface roughness, the positions of neighboring atoms undergo slight variations, causing subtle changes in orbital deformation. Consequently, this variance leads to fluctuations in the strength of the spin-orbit interaction across different local nanomagnets fabricated at different local positions.

Figure (see above) provides a distinct experimental validation of this phenomenon. Keeping other nanomagnet properties constant, a higher kso value signifies a smoother and sharper interface.

(interface roughness & demagnetization ) Why does interface roughness influence the strength of demagnetization field?

A. (2024.03) The impact of surface roughness on demagnetization and, consequently, on magnetic anisotropy is an established experimental observation. In addition to the evidence provided in Fig. 2, there are two more experimental validations. The specifics of the measured modulation of the strength of spin-orbit interaction by a gate voltage (VCMA effect) and by an electrical current (SOT effect) distinctly indicate the significance of influence of surface roughness on demagnetization and the important role of this influence on observed features of those two effects. Detailed data from these measurements will be published in another manuscript and were presented and discussed at the last Intermag conference.

The reason behind the reduction in demagnetization field with increasing surface roughness is straightforward. It is a known fact that the demagnetization field is larger for a smooth plane than for a sphere. A rough surface can be conceptualized as a plane surface covered by spheres. Since each sphere reduces the demagnetization field, the overall demagnetization field of such a rough surface is smaller compared to that of a perfectly smooth surface. Moreover, as the surface becomes rougher, the spheres protrude further from the surface, further reducing the demagnetization field.

(smoother interface & demagnetization) Why is the demagnetization field larger for a smoother interface?

A. (2024.03) The demagnetization field represents the magnetic field of a sequence of the magnetic dipoles, interrupted by the interface. In the scenario of a perfectly smooth surface, this magnetic field aligns precisely along the surface normal at every point. However, in the presence of surface roughness, deviations from the surface normal occur, and these deviations vary slightly across the surface. When averaged, the direction of the demagnetization field remains aligned with the surface normal, but its magnitude reduces. Consequently, the demagnetization field is larger for a smoother surface.

() Questions about oscillations of the strength of spin- orbit interaction

(2024) (about oscillations of the strength of spin- orbit interaction) You observe minor oscillations of the strength of spin- orbit interaction. What is the origin? Does the frequency depend on the material?

The observed oscillations represent unique and unexpected features of the spin-orbit interaction. I am confident that in the future, detailed theoretical and experimental studies will be conducted to explore these intriguing oscillations further. For these forthcoming investigations, the primary linear background can be subtracted to highlight and analyze the oscillatory behavior. However, for the current study, it is imperative to emphasize the main linear dependence as the key finding.

The origin of the observed oscillations in the strength of the spin-orbit interaction remains unknown. One plausible explanation is that the changing distribution of electron orbitals under an external magnetic field is influenced by the different energy levels of neighboring atoms making a slight oscillating variation in the strength of the spin- orbit interaction.

Furthermore, the strength of the spin-orbit interaction is significantly affected by the roughness and sharpness of the interface, as evidenced by clear experimental observations. This implies that the strength of the spin-orbit interaction is highly dependent on the precise positions of atoms at the interface. As the roughness varies slightly from one nanomagnet to another, so does the distribution of atoms at the interface. Therefore, if the oscillations are indeed caused by the influence of neighboring atoms, their amplitude should also vary from one nanomagnet to another.

(origin of SO oscillations) What causes the oscillations in the strength of spin-orbit interaction with an increasing external magnetic field?

A. (2024.03) At present, the origin of the oscillations remains unknown. It is clear that this intriguing phenomenon lacks a simple explanation and deserves further investigation through both theoretical and experimental studies.

One plausible explanation is that the changing distribution of electron orbitals under an external magnetic field is influenced by the different energy levels of neighboring atoms making a slight oscillating variation in the strength of the spin- orbit interaction.

Furthermore, the strength of the spin-orbit interaction is significantly affected by the roughness and sharpness of the interface, as evidenced by clear experimental observations. This implies that the strength of the spin-orbit interaction is highly dependent on the precise positions of atoms at the interface. As the roughness varies slightly from one nanomagnet to another, so does the distribution of atoms at the interface. Therefore, if the oscillations are indeed caused by the influence of neighboring atoms, their amplitude should also vary from one nanomagnet to another. That tendency aligns precisely with experimental data depicted in Figure (See above).

(2024) (about measurements of SO oscillations) You claimed to find the oscillations in the strength of spin-orbit interaction. As this oscillation is not clear, whether it is from the data fluctuations? How did you define the oscillation amplitude?

The observed oscillations exhibit consistent and systematic behavior across all studied nanomagnets. The oscillation amplitude, period, and phase were obtained by fitting the experimental data to a linear function with superimposed oscillations. The evaluated oscillation period and phase were nearly the same for all samples, varying within a narrow range.

The oscillations are clearly an interfacial feature of the spin-orbit interaction, as their amplitude is largest in thinner nanomagnets, where the interfacial contribution dominates, and smallest in thicker nanomagnets, where the bulk contribution predominates.

(2024) (Hso vs. Hext -> linear dependence or  oscillations?) In most equations, the kso is assumed to be the coefffcient of spin- orbit interaction, which does not depend on the external magnetic field. However, oscillation amplitude of the strength of the spin-orbit interaction under an increasing external magnetic field vs. the coefffcient of spin-orbit interaction is hard to explained.

Conservation of T-symmetry requires that the magnetic field of spin- orbit interaction Hso be an odd function with respect to the external magnetic field Hext. Experimental measurements show that the dependence of Hso on Hext exhibits an approximately linear trend with minor oscillations superimposed. While there should be components proportional to H^3 and H^5, these are small and difficult to detect compared to the dominant linear component. The oscillations are clearly an interfacial feature of the spin-orbit interaction, as their amplitude is largest in thinner nanomagnets, where the interfacial contribution dominates, and smallest in thicker nanomagnets, where the bulk contribution dominates.

(possible origin of oscillations) The spin-orbit interaction depends on the shape of the orbital because it determines the degree and specifics of how the external magnetic field breaks the T-symmetry of the orbital. At the interface, the orbital shape is complex and influenced by atoms of two different materials on both sides of the interface. Although the exact origin of the oscillations is still unknown, it can be inferred that such a complex interaction may exhibit some oscillatory behavior.

about Variation of Magnetic Anisotropy and Strength of Spin-Orbit Interaction on Magnetization Reversal

(2024) (about possible influence of hysteresis, remaining domains) The source of the perpendicular magnetic field may be hysteretic. This may explain the difference in strengths of spin-orbit interaction kso and anisotropy field Hani between positive and negative Hz.

The observed effect cannot be attributed to coercivity or hysteresis for several reasons. First, all measurements were conducted under a bias magnetic field Hz ranging from 0.8 kG to 7 kG, which is substantially larger than the coercive fields of the studied FeCoB nanomagnets (20 G to 450 G). Prior to each measurement, the magnetization was fully reversed under a magnetic field of 7 kG, ensuring that the system was well beyond any coercive effects. Second, nearly all the nanomagnets studied are of the single-domain type. These structures lack subdomains even under small magnetic fields or in the absence of a magnetic field, eliminating any contribution from domain-related hysteretic behavior. Thus, the difference in kso and Hani between positive and negative Hz cannot be explained by coercivity or hysteresis but must arise from other intrinsic factors of the system.

(2024) (about possible mechanism of SO dependence on magnetization reversal) Your  measurements highlight that the strength of spin-orbit interaction varies based on the direction of the magnetic field penetration. However, you did not provide a detailed mechanism or theoretical framework to explain why this directional dependence occurs.

The dependency of strength of the spin- orbit interaction on the magnetization direction is not surprising, common and important for the existence of many magnetostatic effects. For example, this dependency is a critical factor for the existence of magnetic anisotropy. Without such a directional dependence, perpendicular magnetic anisotropy (PMA) would not be observed in amorphous nanomagnets. Another key factor influencing magnetic anisotropy is the demagnetization field, which is maximal for perpendicular-to-plane magnetization and nearly absent for in-plane magnetization. In the case of an isotropic spin-orbit interaction, the easy axis and equilibrium magnetization of any nanomagnets is always in-plane. Only when the spin-orbit interaction is stronger in the perpendicular-to-plane direction, the direction of easy axis and equilibrium magnetization can become perpendicular to the plane.

The PMA in FeCoB nanomagnets is known to have an interfacial origin. The directional dependence of spin-orbit interaction for Fe atoms located either in the bulk or at interface has been measured independently (see my AIP2024 paper here). For Fe atoms at the interface, the spin-orbit interaction is significantly stronger in the perpendicular-to-plane direction, while for bulk Fe atoms, it is nearly isotropic, with a slight preference for in-plane directions. Detailed theoretical explanations and calculations of how and why this directional dependence influences magnetic anisotropy are provided in Appendix A of my AIP2024 paper

This directional dependence can also be understood qualitatively. In the bulk of an amorphous nanomagnet, Fe atoms have symmetrical surroundings, resulting in symmetric orbitals and nearly isotropic spin-orbit interaction. At the interface, however, the d-electron orbitals of Fe atoms experience asymmetrical interactions due to the different atomic environments above and below the interface. For example, in Fe/MgO, the Fe orbitals are more strongly influenced by oxygen atoms above than by Fe atoms in the bulk below, leading to a directional asymmetry in spin-orbit interaction strength. This asymmetry explains why the interaction strength differs for in-plane and perpendicular-to-plane magnetization directions.

Similarly, the difference in spin-orbit interaction strength for opposite magnetization directions can also be qualitatively attributed to this orbital asymmetry at the interface. At the Fe/MgO interface, the attractive force exerted by the oxygen atoms above is stronger than the force from the bulk Fe atoms below. Consequently, the Fe orbitals shift asymmetrically toward the oxygen atoms at the interface, resulting in orbital asymmetry with respect to the reversal of the axis perpendicular to the interface.This asymmetry provides a clear origin for the observed effect, although the precise quantitative mechanisms will require further theoretical refinement.

Video of Conference presentations.

67th Annual Conference on Magnetism and Magnetic Materials (MMM 2022)		Intermag 2023. Sendai, Japan
click on image to see YouTube Video		click on image to see YouTube Video
(title): Measurement of strength of spin-orbit interaction		(title): Systematic study of the strength of VCMA effect in nanomagnets of small and large strength of spin-orbit interaction.

Explanation Video

(video): Measurement of coefficient of spin- orbit interaction in a nanomagnet.
(Part 1a): Spin-Orbit (SO) interaction. Perpendicular Magnetic Anisotropy (PMA)   (Part 1c): Internal magnetic field in a nanomagnet   (Part 2): Measurement method of Spin-orbit interaction (SO)  & Perpendicular Magnetic Anisotropy (PMA)   (Part 5a): Analyze of anisotropy field Hani. Measurement of coefficient of spin-orbit interaction kSO       (short content 1:)  the properties of spin-orbit interaction   (short content 1:)  the difference between Global, Local & Average Magnetic Fields.   (short content 1:)  how it is possible to measure  the strength of SO and strength of PMA.    (short content 1:) analyze the measurement of the anisotropy field (short content 2:)   linear relation between the external magnetic field and Hso and about the symmetry and physics arguments, which are behind this linear relation   (short content 2:)  how to measure experimentally the internal magnetic field Hint   (short content 2:)    what holds  the magnetization along the easy magnetic axis and how to measure the strength of the holding force.   (short content 2:)  the measured oscillations of Hani and why this oscillation is an important characteristic of a nanomagnet (short content 3:)   how the deformation of the orbital at the interface creates the perpendicular magnetic anisotropy (PMA)   (short content 3:) experimental measurements of Hint in FeB nanomagnets.   (short content 3:)   the experimental setup and main idea behind the proposed measurement   (short content 3:)   why the spin-orbit interaction depends on the polarity of the magnetic field and how to measure it.
Other parts of this video set is here
click on image to play it