Dr. Vadym Zayets
v.zayets(at)gmail.com
My Research and Inventions
click here to see all content |

Dr. Vadym Zayetsv.zayets(at)gmail.com |
|
 |
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
|
sp-d exchange interaction
Spin and Charge TransportAbstract:The sp-d exchange interaction is the spins of localized d-electrons and conduction delocalized sp-electrons. Due to the sp-d exchange interaction, the conduction sp- electrons and localized d-electrons align their spins in the same direction (common case) or antiparallel directions (rare case). main contribution to the sp-d exchange interaction is the scatterings between conduction and localized electrons. Also, there is a direct exchange interaction between conduction and localized electrons due to the overlap of their wave functions. This type of the exchange interaction is significantly disturbed due to movement of the conduction electrons in space. For this reason, such exchange interction is stronger for the standing-wave conduction electrons.
Exchange interaction between localized and delocalized electronsThe sp-d Exchangre interactionExchange interaction between localized and delocalized electrons is very important because:(1) In a ferromagnetic metal it makes an electron gas to be spin-polarized In a ferromagnetic metal, spin directions of all localized electrons (d- and f- electrons) are in one direction. Because of the exchange interaction some of delocalized (conduction) electrons become spin- polarized in the same direction. (2) It is the origin of the spin torque. The spin polarization of electron gas can be transferred from a point to a point in a metal by (1) A drift current. It is not effective method in a bulk of the metal. It becomes more effective in the vicinity of an interface (2) The Hall effect. It is a very efficient method for the spin transfer. The spin transfer occurs due to the ordinary hall effect, the spin Hall effect or Anomalous Hall effect When the spin direction of delocalized (conduction) electrons or their amount (the spin polarization) are different from an equilibrium, the exchange interaction induces the spin torque. Origin of the the sp-d Exchangre interactionSeveral are several different origin : 1) the scatterings between conduction and localized electrons; 2)direct exchange interaction between conduction and localized electrons due to the overlap of their wave functions due to the overlap of their wave functions 3) dipole interaction due to the magnetic field induced by the spins
Direct exchange interaction between conduction and localized electronsdue to the overlap of their wave functions
This exchange interaction is similar to the exchange interaction between the localized electrons. Similary it has 3 contributions: 1)
The exchange interaction between localized and delocalized electrons significantly depends on sizes of localized and delocalized electrons. therefore, it is different from material to material. The size of localized electrons equals to the shortest distance between atoms in the metal The size of localized and delocalized electrons equals to the mean-free path.
The exchange interaction with localized electrons is significantly different for standing-wave and running-wave electrons.
1.Direct exchange interaction between delocalized and localized electrons.. This type of the exchange interaction is major exchange mechanism between localized electrons (See above) Since significant difference between special distributions of the localized and delocalized electrons, the antiferromagnetic exchange interaction due to vanishing of the Coulomb repulsion for identical electrons of opposite spins is small for them. The Exchange between running-wave electron and localized electrons Since position of localized electrons does not change in time, but the position of running-wave electrons changes, the polarity of exchange interaction changes in time as a running-wave electron passes near by a localized electron (See Fig.7). It makes weak the exchange between running-wave electron and localized electrons. The Exchange between standing-wave electron and localized electrons In this case both electrons does not move and the exchange interaction may be substantial. this exchange mechanism is the major mechanism of the inter layer exchange coupling. The standing-wave electrons forms in the vicinity of an interface and multi layer structures. For example, in Co/Ru/Co there is a substantial antiferromagnetic exchange interaction between Co layers at Ru thickness of 0.9 nm. The distance of 0.9 nm is too long for a direct exchange interaction between localized electrons of Co of different Co layers. Because of the electron reflection at each Ru/Co layer, there is a significant amount of the standing-wave electrons in the Ru layer. The Coulomb repulsion of between localized d-electrons of Co and standing-wave electrons of Ru is smallest when magnetization of Co layers are opposite (spins of d-electrons of Co are opposite for Co of different layers) Q. Is it possible to explain this effect by the direct interaction between localized electrons of Co and Ru and between different localized electrons of Ru. A. This effect is called the magnetic proximity effect (See here) and it may contribute, but the contribution is not large. It can be concluded from the experimentally-measured thickness dependence. It changes its signs with thickness. It could be possible only when the exchange between localized electrons of Ru is antiferromagnetic (it is very unlikely, because of small size of localized electrons in Ru). Importantly, the sign of exchange interaction should be opposite with addition of one mono layer of Ru (as in the case of Cr), but it is not the case.
2. The exchange interaction between delocalized and localized electrons due to scatterings
Because of this exchange interaction the electron gas in a ferromagnetic metal is spin-polarized.
3. Aligning of spins along internal magnetic field (antiparalel to the magnetization). Dipole interaction.
|
 |
Fig 4. Animated figure. Precession of spins of the local d-electrons (red arrow) and conduction electrons (blue arrows) due to exchange exchange interaction. Black line shows the rotation axis. The angle between spin directions is 70 deg. Angle of spin direction to rotation axis is 20 deg for d-electrons and 50 deg for sp-electrons. |
It should be noted that the Hamiltonian (30a) describing the exchange interaction is similar to the Hamiltonian describing the interaction of the conduction electrons with a magnetic field H
![]()
Therefore, the results obtained in the previous section for the interaction of electron with the magnetic field can be applied for the description of the exchange interaction.
Similarly to previous section, the conduction electrons can be described by two representations. In the first representation the electron wavefunction is described as a combination of two wave functions corresponding to different energies
![]()
which are energies in the cases when the spin direction of a conduction electron is parallel and anti parallel to the spin direction of the d-electrons. In the second representation, the single energy of the conductive electrons equals to E_0 and there is a precession of the spin of the conduction electron around the axis, which is along the spin direction of d-electrons. Similar to Eq. (28) the precession frequency can be expressed as
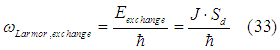
Figure 3 shows precession of spin of a conduction electron about the axis, which is along the magnetization direction of the d-electrons.
Precession shown in Fig. 3 corresponds the case when the total spin of d-electrons is significantly larger than spin of conduction electrons. In the case when spins are comparable, there is a precession of both the conductive electrons and d-electrons about the axis, direction of which is between the spin directions of the d-electrons and the spin direction of the conduction electron. (See Fig. 4)
The d-electrons might experience the exchange force from several conduction electrons simultaneously. Therefore, the precession frequency will be
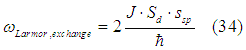
where 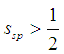
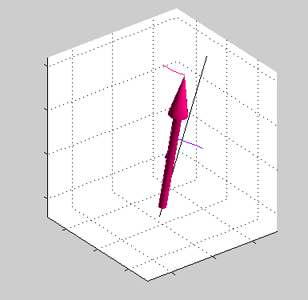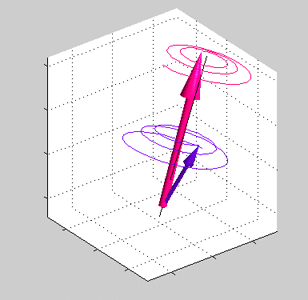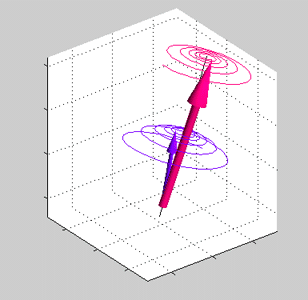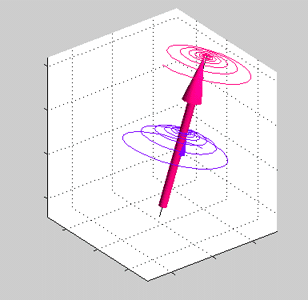 |
Fig 5. Animated figure. Damping of the precession of spins of the local d-electrons (red arrow) and conduction electrons (blue arrows) in an exchange field. J>0. Both precessions of spin of the local d-electrons and spin of the conduction sp-electrons are damping towards a common axis of the precession (black line) |
Comparing Hamiltonians of Eqs. (30a) and (31), the exchange interaction can be described by the effective magnetic field (historically it is called the molecular field of Weiss)
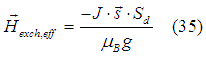
Similar to the case of spin in an external magnetic field, in the exchange field the spin precession is damped. The damping is described by the Landau-Lifshiz equation
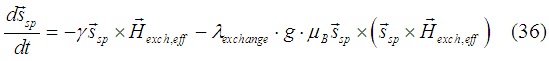
Because of the precession damping, the spins of the conduction sp-electrons and the local d-electrons are aligned with each other.
![]()
![]() I am strongly against a fake and "highlight" research
I am strongly against a fake and "highlight" research ![]()
![]()
![]()
![]()
![]()
![]()
I will try to answer your questions as soon as possible