Measurement of Magnetic and Magneto- transport properties of FeCoB nanomagnets

Spin and Charge Transport

Abstract:

Detailed measurement data (including all raw data ) of magnetic and magneto- transport properties of FeCoB nanomagnets are described. 3 new high- precision, high- reproducibility, high- repeatability measurements have been used. I have developed these methods in 2018-2020. The 1st method measures the dependence of the Hall angle on external magnetic field, which is applied along the magnetization of the nanomagnet. It allows a high- precision measurement of the Inverse Spin Hall effect (ISHE) and Anomalous Hall effect (AHE). Additionally it allows to evaluate different spin properties of the electron gas (e.g. the spin polarization). The 2nd method is the modified measurement of the anisotropy field H_ani, where the in-plane component of magnetization is measured by scanning both in-plane and perpendicular- to- plane external magnetic field. Additionally the method measures the strength and features of perpendicular magnetic anisotropy (PMA) and current induced in-plane magnetic field, which is called "damp- like torque" and "field-like" torque. The 3nd method is a high- precision measurement of parameters of thermo- activated magnetization switching such as coercive field, retention time, size of nucleation domain and parameter delta.

Exploring a very high precision of the developed measurement methods, the dependence of the magnetic parameters on gate voltage (the voltage- controlled magnetic anisotropy (VCMA) effect) and the current (spin- orbit torque (SOT) effect) was precisely measured and studied.

Single-layer nanomagnet. Optical lithography only.

nanomagnet size 3um x 3 um

wafer	Volt40	Volt54A	Volt57A	Volt57B	Volt58A	Volt59A	Volt 47B
nanomagnet, nm	FeB(1.3)	FeB(1.1)	FeCoB(1.1) x=0.5	FeCoB(1.1) x=0.5	FeCoB(1) x=0.3	FeB(0.9)	FeB(1.2)
nanowire, nm	Ta(2)	Ta(2.5)	Ta(5)	Ta(5)	Ta(5)	Ta(8)	W(3)
Anisotropy field H_ani, kG	4.0~4.3	2.6~2.8	4.3~4.6	4.4~4.6	6.4~7.2	6.5~9.5	2.5 ~2.75
spin-orbit interaction k_SO	-0.5 ~ -0.1	-0.24 ~ -0.18	-0.4 ~ -0.1	-0.2 ~+0.05	-0.55 ~ -0.3	-0.5~+0.4	-0.15 ~ -0.06
Coercive field H_c, Oe	170 ~220	30	200~325	620~740	275~325	280~550	80 ~ 90
Conductivity S/m2	0.028-0.033	0.055-0.06	0.044-0.055	0.02-0.027	0.048-0.051	0.048-0.052	0.06 ~0.068
Size of nucleation domain, nm	37~48	small	48~60	34~45	48~58	46~62
log(retention time/1s)	6~21	small	38~45	24~36	28~42	28~34
delta	100~140	small	160~260	90~140	300~325	190~380

click on wafer name to see more detailed data

Single-layer nanomagnet. Electron lithography.

width of nanomagnet is 100 nm or 200 nm or 400 nm or 1000 nm or 2000 nm

length of nanomagnet is 50 nm or 100 nm or 200 nm or 400 nm or 1000 nm or 2000 nm

wafer	Volt50B	Volt53B	Volt54B	Volt55	Volt59B
nanomagnet, nm	FeB(1.1)	FeCoB(1) x=0.3	FeB(1.1)	FeB(0.9)	FeB(0.9)
nanowire, nm	Ta(3)	Ta(2.5)	Ta(2.5)	Ta(5)	Ta(8)
Anisotropy field H_ani, kG	4.45~ 4.75	3.0~ 5.0	1.75 ~ 2.2	3.0~ 8.0
spin-orbit interaction k_SO	+0.05~+0.3	-0.4~+0.25	-0.4~+0.3	-0.3~ +1.5
Coercive field H_c, Oe	145~220	200~325	5~50	100~ 400
Conductivity S/m2	0.039-0.062	0.039-0.047	0.037-0.06	0.028-0.038
Size of nucleation domain, nm	30-55	40~65	small	22~85
log(retention time/1s)	6~16	10~25	small	5~ 28
delta	80~200	100~250	small	40~ 800

Multi-layer nanomagnet. .

nanomagnet size 3um x 3 um

wafer	Volt39A	Volt45B	Volt48A	Volt43A (EB)	Volt44B (EB)
nanomagnet, nm	FeB(0.8):Ta(0.5):FeB(0.8)	[FeB(0.55) W(0.5)]5 FeB(0.55)	[FeB(0.45)/W(0.2)]7 FeB(0.45)	FeB(0.8): W(1.5): FeB(0.8)	FeB(0.8):W(0.5): FeB(0.8):W(0.8):FeB(0.8)
nanowire, nm	Ta(2)	W(3)	W(3)	Ta(2)	Ta(2)
Anisotropy field H_ani, kG	2.6~3.7	7 ~8	7.9 ~8.3	5.5 ~8.2	6.0~9.0
spin-orbit interaction k_SO	+0.9 ~ +2.6	+2 ~ +2.5	+0.9 ~ +1.2	+0.45 ~ +0.8	+0.42 ~ +0.85
Coercive field H_c, Oe	10	150 ~ 250	40	250	250
Conductivity S/m2	0.035~0.037	0.043 ~0.047	0.047~0.049	0.04 ~0.07	0.005 ~0.008
Size of nucleation domain, nm
log(retention time/1s)
delta

click on wafer name to see more detailed data

Content

click on the chapter for the shortcut

Measurement method: Hall effect

Using Hall measurements, it is possible to measure very small nanomagnet without any external disturbance. Magnetic and magneto transport properties can be measured for nanomagnet as small as 30 nm x 30 nm.

Modulation methods: gate voltage or bias current

in order to avoid a systematical error magnetic properties of a nanomagnet should be modulated and change of properties should be detected

Modulation by gate voltage

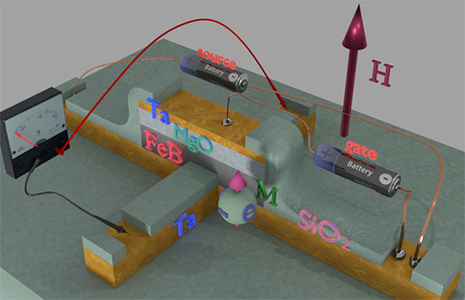Magnetic properties of nanomagnet (FeB, shown in grey) are changed when a gate voltage is applied at a metal- isolator interface at the top of the nanomagnet. The source battery provides the bias current through the metallic nanowire and the nanomagnet. The voltmeter measured the Hall voltage, which is created perpendicularly to the bias current. The gate voltage is applied between the top of nanomagnet and the nanowire. Because of thick (~ 10 nm) gate isolator (MgO), the gate voltage does not induce any electrical current. The gate modulation does not change the temperature of the nanomagnet. It is the main merit of the modulation of the magnetic properties of nanomagnet by a gate voltage. The effect, which describes the dependence of the magnetic properties on the gate voltage, is called the Voltage- Controlled Magnetic Anisotropy (VCMA). See details here.

Modulation by bias current

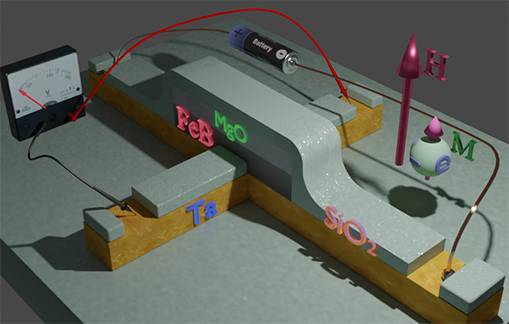Magnetic properties of nanomagnet are changed when the value of bias is changed. The source battery provides the bias current through the metallic nanowire and the nanomagnet. The voltmeter measured the Hall voltage, which is created perpendicularly to the bias current. Since the used current density is relatively large ~ 50 mA/um2 (otherwise the Hall voltage is to small to detect), the temperature of the nanomagnet is changed when the magnitude of the current change. Additionally, the magnetic properties of the nanomagnet depend on the polarity of the current. This effect is called Spin- Orbit Torque (SOT). (See details here)

Ferromagnetic metal (FeB) is shown in grey. Non- magnetic metal (Ta) is shown in yellow color. Non-conductive isolator (SiO2) is shown in green. The used width of nanowire is between 50 nm and 3000 nm. The used length of nanomagnet is between 30 nm and 3000 nm. Due to the nano size of the FeB, its magnetization is always in single- domain state (parallel over whole volume). Therefore, the nano- sized FeB is called a nanomagnet. The magnetization of nanomagnet (FeB) is perpendicular to plane and is shown as green ball with red arrow. External magnetic field (red arrow) is applied either perpendicularly- to- plane (as shown) or in- plane.

Images made by Scanning Electron microscope SEM) of fabricated devices

On Ta nanowire (width 500 nm) (f

Top

click on image to enlarge it

(1) Raw Measurement Data of all nanomagnets

() Measurement methods

(method 1): Measurement of Anomalous Hall effect (AHE) and Inverse Spin Hall effect (ISHE)

(method 2): Measurement of anisotropy field, strength of perpendicular magnetic anisotropy (PMA), " field- like torque" and "damp- like torque"

(method 3): measurement of coercive field, retention time, size of nucleation domain and parameter delta.

(2) Measurement of Voltage- Controlled Magnetic Anisotropy (VCMA effect)

(3) Temperature dependence of magnetic parameters

(4) Measurement of Spin- orbit torque (SOT effect)

(5) Measurement in gate and gap regions.

(b) VCMA

(11) Volt59B: Ta(8 nm)/ FeB(0.9 nm) H_anis=6 -9 kG H_c=220 Oe-290 Oe

(a) SOT

(b) VCMA

(12) Volt 39A Ta(2):FeB(0.8):Ta(0.5):FeB(0.8):MgO(5): Ta(1): Ru(5)

(13) Volt 48A [FeB(0.45)/W(0.2)]7 FeB(0.45) MgO(6.5)/W(1)/Ru(5)

(11) Questions & Answers

.........

Measurement Data of all nanomagnets

newest:

June 2022 nanomagnet2022.06.12.zip

old

January 2022 nanomagnet2022.01.10.zip

July 2021 2021.07.01.zip

April 2021 data nanomagnet 2021.03.zip

Data of All nanomagnets

PMA & strength of the spin-orbit interaction

click on image to enlarge it

Coefficient of spin-orbit interaction k_SO vs. anisotropy field H_ani	Internal magnetic field vs. coefficient of spin-orbit interaction k_SO

For a single-layer or double-layer nanomagnets, the slope is positive. For a multilayer nanomagnets (green and blue stars), the slope is negative.	The effective magnetic field decrease with the increase of k_SO. It is because the interface smoothness, which leads to a larger H_SO and k_SO, also leads to a larger demagnetization field.

Amplitude of oscillation of H_ani vs. anisotropy field H_ani	Amplitude of oscillation of H_anivs. coefficient of spin-orbit interaction k_SO	Amplitude of oscillation of Hani. vs. coefficient of spin-orbit interaction k_SO

	Oscillation amplitude and k_SO simultaneously become larger. It is because they both are originated by the interface. When the contribution of the interface becomes larger and the contribution of the bulk becomes smaller, both the oscillation amplitude and k_SO become larger.	the same as the left figure, but with a different scale.

Measurement methods

All measurement method have been developed by me in 2018-2020. The features of all methods are a high- repeatability, high-reproducibility and very high measurement precision. I do my best to avoid and eliminate any possible systematical error.

3 measurement methods to characterize magnetic and magneto- transport properties of a nanomagnet

Measurement methods 1 & 3

Measurement method 2

A hysteresis loop is measured as a scan of perpendicular magnetic field H_z . (method 1) From dependence of measured Hall angle on , magnitudes of Anomalous Hall effect (AHE) and Inverse Spin Hall effect (ISHE) are measured. Spin properties of conduction electrons are evaluated. (method 3) From

(method 2) An external magnetic field (in- plane field H_||) i applied perpendicularly to the stable magnetization (easy axis) of the nanomagnet (perpendicular- to plane). Even though the magnetization is turning towards and away from its the equilibrium direction (easy axis), it resists against the turning. Method 3 measures the strength of this resistance and therefore the magnetic energy, which contains in the nanomagnet. An. additional magnetic field H_z is applied to enhance the resistance against the turning and therefore it more clarifies the magnetic features of the nanomagnet.

All three measurements were developed and optimized in 2019-2020. The features of all methods are a high- repeatability, high-reproducibility and very high measurement precision.

Click on image to enlarge it

(high repeatability, high reproducibility)I have checked re measured some random samples after ~one year after their first measurement. All measurements gave exactly same results with the measurement precision.

(high measurement precision)I have achieved a very high measurement precision for all my methods. E.g. I can measure the coercive field with precision of 0.1 Oe (See here) , which is very hard to achieve by any other known measurement methods. I am constantly improving my measurement setup in order to reduce measurement noise and therefore to improve the measurement precision.

(free of a systematic error)To avoid a systematical error is the major challenge for any high- precision measurement method. In order to avoid a systematical error, I time- to time verify a measurement by several independent measurement method. Achievement of the same value of the parameter measured by independent methods is a good indication that there is no systematical error.

(measurement method 1): Fit

Hall angle α_Hall vs. external perpendicular magnetic field	1st derivative	2nd derivative

Simultaneous fit for 0, 1st and 2nd derivatives are perfect.

There are always some oscillations for 2nd derivative. As 2020.04, their origin is unknown.

Sample Volt 54B free 28

Click on image to enlarge it

The method 1 is very difficult to use (or even impossible to use) for a larger- size nanomagnet or a continuous film due to their domain structure.

Is it possible to detect the existence of the static domains from this measurements?

A. Yes.

(indication 1 for existence of static domains): there are sharp peaks for 1st and 2nd derivatives

(indication 2 for existence of static domains): the fitting is impossible

(indication 3 for existence of static domains): red,green, blue and light- blue lines of Fig.11 do not coincide

(measurement method 1): Measurement of AHE and ISHE contributions. Sample- to- sample dependence

Hall angle α_Hall vs. external perpendicular magnetic field	1st derivative	2nd derivative

Device- to- device difference is substantial due to a large difference of α_AHE	Device- to- device difference is small due to a small difference of α_ISHE	Device- to- device difference is similar (corresponded) as for 1st derivative

The measurement clearly indicate that AHE change substantially and ISHE nearly does not change from a device to device

Note: some samples show a substantial device- to- device difference of both α_AHE and α_ISHE. . See below detailed measurements for each sample

Sample Volt 54B

Click on image to enlarge it

(note) There is an ambiguity of the fitting α_Hall and its 1st and 2nd derivatives (See here), when exactly the same fitting can be obtained at different sets ( α_AHE, α_ISHE , sp), where α_AHE is the magnitude of Anomalous Hall effect (AHE), α_ISHE is the magnitude of Inverse Spin Hall effect (ISHE) and sp is the spin polarization of the electron gas.

(note) Often the difference of the α_Hall between different nanomagnets of the same sample is a constant offset of α_Hall without a change (or with a very small change) of its 1st and 2nd derivatives (E.g. sample Volt54). It indicates that there is a difference of magnitude of AHE between samples, but the variation of the ISHE and spin polarization sp of the electron gas is weak from a nanomagnet to nanomagnet .

(note 2): There are sample where it is not the case (See details of each sample)

(measurement method 1): Measurement of AHE and ISHE contributions. Current dependence

Hall angle α_Hall vs. external perpendicular magnetic field	1st derivative	2nd derivative

difference is substantial due to a large current- dependence of α_AHE	difference is small (negligible) due to a tiny current- dependence (nearly independence) of α_ISHE	Device- to- device difference is similar (corresponded) as for 1st derivative

The measurement clearly indicate that the current change substantially AHE, but it nearly does not influence ISHE

Note: some samples show a substantial- current dependence of both α_AHE and α_ISHE. See below detailed measurements for each sample

Sample Volt 54B free 28

Click on image to enlarge it

(note) There is an ambiguity of the fitting α_Hall and its 1st and 2nd derivatives (See here), when exactly the same fitting can be obtained at different sets ( α_AHE, α_ISHE , sp), where α_AHE is the magnitude of Anomalous Hall effect (AHE), α_ISHE is the magnitude of Inverse Spin Hall effect (ISHE) and sp is the spin polarization of the electron gas.

(note): For the most of sample (E.g. Sample Volt 54B free 28), a different gate voltage or bias current makes a constant change of α_Hall without a change (or with a very small change) of 1st and 2nd derivatives. It indicates that the gate voltage or bias current mainly influence the AHE and only weakly influence the ISHE and spin polarization sp of the electron gas.

(note 2): There are sample where it is not the case (See details of each sample)

(measurement method 1): Separation and calculation of AHE and ISHE contributions. Current dependence

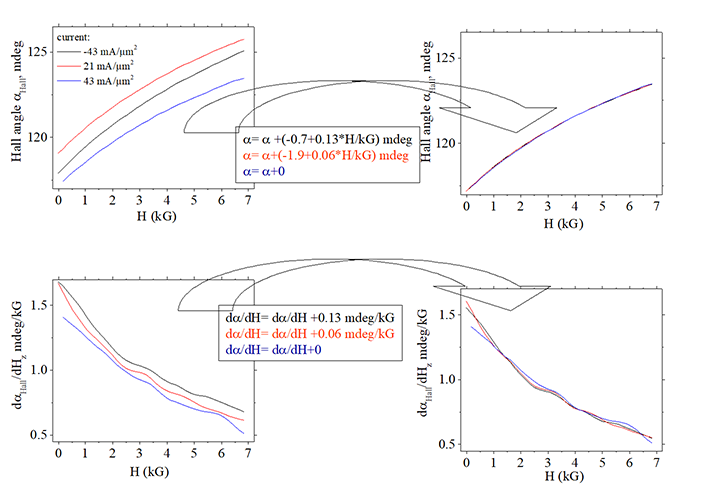(left side: Measured data) : Both α_Hall and dα_Hall /dH_z depend on the current

(right side: data fitted to each other) : (step 1) (right- bottom graph): fitting of 1st derivative dα_Hall /dH_z measured at different currents into one single line (step 2) (right- top graph):. Fitting of measured α_Hall at different currents into one single line. After two steps all lines fit perfectly in one single line._.

Note: 2nd derivative behaves similar to 1st derivative

Note: Lines for different current perfectly coincides to each other for 0 and 1st derivatives

When current j is change from 43 to 23 mA/ μm², AHE change is Δα_AHE =-1.9 mdeg and change of derivative ISHE Δ(dα_ISHE/dH)= 0.06 mdeg/kG

When current j is change from +43 to -43 mA/ μm², AHE change is Δα_AHE = -0.7 mdeg and change of derivative ISHE Δ(dα_ISHE/dH)= 0.13 mdeg/kG

Sample: Volt57B L20

Fig.31. Click on image to enlarge it

Due to the an ambiguity of the fitting α_Hall (See here), it is difficult to calculate the absolute values of the magnitude α_AHE of Anomalous Hall effect (AHE), the magnitude α_ISHE of Inverse Spin Hall effect (ISHE) and the spin polarization sp of the electron gas. However, it is possible to measure their relative changes under a different gate voltage or bias current or a changes from sample to sample

Figure 31 shows measured data of sample, in which both α_Hall and its 1st derivative change for a different bias current. The measured data are shown at right side of figure. It is clear that current dependences for α_Hall and its 1st derivative are different and independent.

(note) the current dependence of the 2nd derivative (not shown) is similar to the current dependence of the 1st derivative

It can be assumed that the bias current only affects α_AHE and α_ISHE other parameters, which may influence α_Hall , remain unchanged.

(step 1). Since α_AHE is a constant vs H, the 1st derivative (and 2nd derivative) is proportional to α_ISHE and is not influenced by α_AHE. Lines of left- bottom graph are clearly parallel and their difference is a constant. Adding a constant to 1st derivative, it is possible to fit all lines, which corresponds to 1st derivative at a different current, to one single line (See bottom right graph). It gives the difference of magnitude Δα_ISHE of ISHE at a different currents

(step 2) After correction of α_Hall for , the lines in top- left graphs becomes parallel and and their difference becomes a constant. Adding corresponded constant to each line, it is possible to fit all lines to one single line (See top- right graph). It gives the difference of magnitude Δα_AHE of AHE at different currents

(method 2): Measurement of anisotropy field, strength of perpendicular magnetic anisotropy (PMA), " field- like torque" and "damp- like torque"

Method 2: Measurement of PMA strength

(*measurement the strength of PMA) FeB nanomagnet is fabricated on top of Ta nanowire. A pair of Hall probes is aligned to the nanomagnet. When an electrical current through the nanomagnet, there is a Hall voltage, which is linearly proportional to to perpendicular component of the magnetization. The nanomagnet magnetization is shown as the green ball with arrow. The equilibrium magnetization direction is perpendicularly to plane. When an external in-plane magnetic field H_\|\|* is applied, the magnetization turns towards H_\|\|. The field, at which the magnetization turns fully in-plane, is called the anisotropy field H_ani and it is linearly proportional to the PMA energy. The *left figure* shows measured in-plane component of magnetization M_\|\| vs H_\|\|. The dependence is linear. From its slope the H_ani is evaluated. To evaluate features of the PMA, an additional external perpendicular magnetic field H_z is applied during a scan of H_\|\|. The right figure shows H_ani vs H_z . The H_ani increases under H_z.
( H_ani *as a measure of PMA* energy) Due to the PMA, the lowest - energy states (easy axis) is when the magnetization is perpendicularly to the plane, and the highest - energy states (hard axis) when the magnetization is in- plane. The in- plane magnetic field reduces the in-plane energy. When the in-plane energy becomes smaller than perpendicularly -to plane energy, the magnetization turns fully in-plane.
(*additional measurement: measurement of SOT effect) The line of measured dependence M_\|\|* vs H_\|\| (left figure) does not through axis origin. It indicates that additionally to the external in-plane magnetic field *_\|\|, there is an intrinsic in-plane magnetic field H_off. The H_off* is proportional to electrical current. The H_off originates by the effect of Spin- Orbit Torque (SOT). (See details here).
Note. I have developed this measurement method in 2019-2020
click on image to enlarge it

(measurement method 2): Measurement of H_anis, PMA strength, " field- like torque" and "damp- like torque

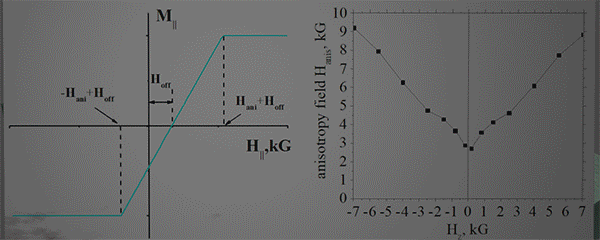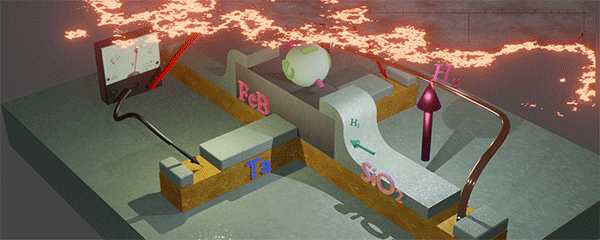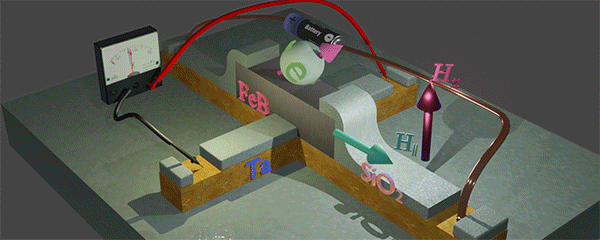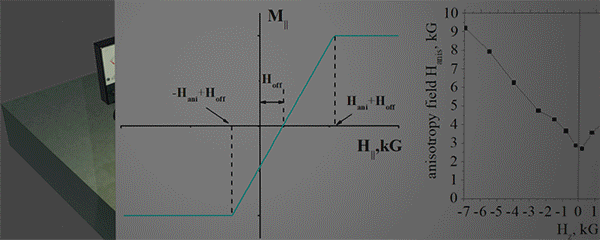
External magnetic field H_|| is applied in-plane and perpendicularly to the magnetization (along the hard axis). As a result, the magnetization turns towards the magnetic field. The magnetic field, at which the magnetization turns completely in-plane, is called the anisotropy field H_anis . The H_anis is a measure of the strength of the perpendicular magnetic anisotropy (PMA). In order to characterize the features of the PMA, an additional field H_z is applied perpendicularly to the film

(what is measured)

(parameter 1) The anisotropy field H_anis. which characterized the strength of perpendicular magnetic anisotropy (PMA); (parameter 2) In- plane magnetic field, which might be induced by an electrical current or PMA. The in-plane magnetic field is measured as the offset magnetic field H_off for the H_|| scan.

(which parameters are evaluated)

Anisotropy field, the strength of spin- orbit interaction, which induces PMA, demagnetization field and parameters of the spin- orbit torque (SOT) such as the current- induced in- plane magnetic field, "damp- like" torque and "field-like" torque.

Note. I have developed this measurement method in 2019-2020

Click on image to enlarge it

(main idea): In-plane component of magnetization M_|| is measured under an in-plane external magnetic field H_||. In absence of the magnetization M is perpendicular to the plane. Under H_|| the M turns towards H_|| until its direction is fully in-plane. The stronger the PMA is, the large H_|| is required to turn M fully in- plane.

(How does it work)An external magnetic field (in- plane field H_||) i applied perpendicularly to the stable magnetization (easy axis) of the nanomagnet (perpendicular- to plane). Even though the magnetization is turning towards and away from its the equilibrium direction (easy axis), it resists against the turning. Method 3 measures the strength of this resistance and therefore the magnetic energy, which contains in the nanomagnet. An. additional magnetic field H_z is applied to enhance the resistance against the turning and therefore it more clarifies the magnetic features of the nanomagnet.

(Which parameters are measured) Two parameters are measured: (parameter 1) Angle of line M_|| vs H_||, which gives the anisotropy field H_ani The H_aniis the field at which the line crosses the x-axis and therefore the magnetization is aligned fully in- plane. (parameter 2). The offset magnetic field H_off, . The H_off is the magnetic field, for which the line is shifted from the axis origin.

(measurement method 2): Measurement of H_anis, PMA strength, " field- like torque" and "damp- like torque

scan at different perpendicular magnetic field H_z	scan at one fixed H_z	scans at two fixed H_z

Click on image to enlarge it

(What is new in the proposed measuremengt method) Two

(old measurement method): in-plane magnetization M_|| is measured under scan of H_|| without any perpendicular field H_z

(new proposed measurement method): in-plane magnetization M_|| is measured under scan of H_|| at a different perpendicular field H_z

(measurement method 2): Offset magnetic field H_off vs perpendicular magnetic field H_z

Offset magnetic field H_off vs perpendicular magnetic field H_z. Scan of H_\|\| is along current	Offset magnetic field H_off vs perpendicular magnetic field H_z. Scan of H_\|\| is perpendicular to current

Sample Volt40 R73	Sample: Vot54A L20B
It measure a component of offset magnetic field, which direction is along nanowire	It measure a component of offset magnetic field, which direction is perpendicular to nanowire

Click on image to enlarge it

(fact 1) There is in- plane magnetic field in ferromagnetic nanomagnet, which induced by PMA effect at boundaries of the nanomagnet.

(fact 2) The magnitude and direction in- plane magnetic field H_offincreases and changes direction when an external magnetic field H_z is applied perpendicularly- to- plane of the nanomagnet

fact 3) The magnitude and direction of in- plane magnetic field H_off are different for opposite polarities of the external magnetic field H_z It indicates

Can the offset magnetic field H_off be created due to a possible misalignment of the measured sample with respect to the magnet? Misalignment of perpendicular magnetic field H_z of only 0.5 deg from the film normal will induce in- plane field H_|| of 10 G at H_z=7 kG?

A. I have calibrated magnet with precision about 0.1 Oe by measuring the Hall effect in non-magnetic metal Ru (See below).

(measurement method 2): Offset magnetic field H_off vs perpendicular magnetic field H_z

Offset magnetic field H_off vs perpendicular magnetic field H_z. Scan of H_\|\| is along current	Offset magnetic field H_off vs perpendicular magnetic field H_z. Scan of H_\|\| is perpendicular to current

Sample Volt40 R73	Sample: Vot54A L20B

Click on image to enlarge it

Destinguishing the type of magnetic field

A magnetic field creates a torque on magnetic torque

(type 1 of magnetic field) "Field - like torque"

Measurement of anisotropy field H_ani

Soft sample (Volt54A R42C)	Hard sample (Volt58A R41C)	From many different samples

H_ani = 2.5 kG	H_ani = 7 kG	Each nanomagnet has a different H_ani and different slope. However, for nanomagnets, which fabricated on the same waver, H_ani and slopes are about the same (with exceptions, See data below for each wafer)

Anisotropy field H_ani for a nanomagnet is defined as the minimal point at H_z =0.

The dependence diverse from a linear and contains some oscillation of an unknown origin in region |H_z|< 2kG

anisotropy field is calculated from the slope of dependence M_|| vs H_||(See above)

Click on image to enlarge it

Measurement of anisotropy field H_ani on gate voltage (VCMA effect)

Soft sample (Volt54A R42C)	Hard sample (Volt58A R41C)

Click on image to enlarge it

verification of required measurement precision. Click here to expand.

Verification of required measurement precision

(Verification experiment for magnetic alignment)):

Hall angle α_OHE of Ordinary Hall effect in non- magnetic ruthenium (Ru) for different values of in-plane magnetic field H_\|\| applied along current	Hall angle α_OHE in non- magnetic Ru for different values of in-plane magnetic field H_\|\| applied is perpendicularly to current

Sample: Ref30 (Ru 25 nm). Rotation angle (dα_OHE/dH_z=-3.7 mdeg/kG)

Click on image to enlarge it

Content

(method 3): measurement of coercive field, retention time, size of nucleation domain and parameter delta

Measurement method 3:measurement of parameters of thermally- activated switching

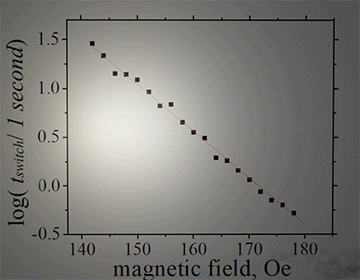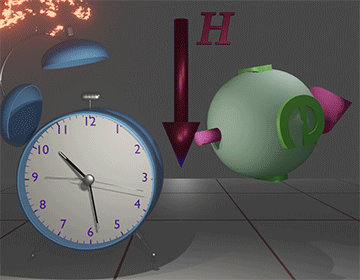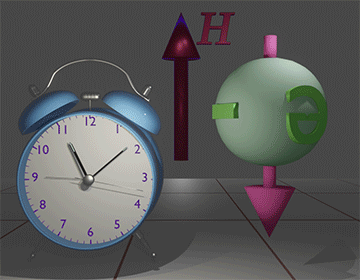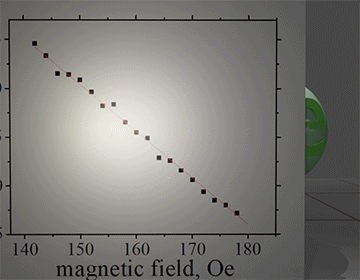(measurement method): A magnetic field is applied opposite to the magnetization and the time until the magnetization switching is measured. The switching time is exponentially depends on the intensity of the external magnetic field. From this dependence all parameters of the thermally activated switching are measured, which include coercive field, retention time, parameter delta, size of a nucleation domain
(thermally-activated switching): There is an energy barrier between two stable states for magnetization of a nanomagnet. The magnetization switches between the states only by assistance of a thermal fluctuation of an energy higher the barrier height. The probability of the thermal fluctuation is exponentially proportional to its energy. The magnetic field reduces the energy barrier. This is the reason why the switching time exponentially proportional to the magnetic field.
(features of the method): high precision; high repeatability, high reliability
Note. I have developed this measurement method in 2017-2018
click on image to enlarge it

(main idea): All parameters of for thermo- activated switching such as coercive field, retention time, size of nucleation domain and parameter delta are measured by measuring an average switching time between two magnetization directions

(measurement method 3): Measurement of coercive field H_c, retention time, size of nucleation domain and parameter delta

	thermo- activated magnetization switching	measurement of switching time

(what is measured) The magnetization switching time vs magnetic field, which is applied opposite to the magnetization	Due to thermo fluctuations, the magnetization is switched periodically between its two stable directions (e.g. up and down). The average time of the magnetization switching is called the retention time τ_ret.	measurement method: All parameters: H_c, τ_ret, size of nucleation domain and parameter Δ are evaluated from a measurement of magnetization switching time as the function of an external magnetic field.

(which parameters are evaluated)

Coercive field H_c, retention time τ_ret, size of nucleation domain and parameter Δ

I have developed this method in 2018-2020

click on image to enlarge it

Why this method has the highest repeatability, reproducibility and precision for the measurement of the magnetization switching parameters? What are the problems of the alternative methods?

There are two reasons why other measurement methods a suffer from systematical errors.. The reason one is that the main parameter of the magnetization switching is the time interval, after which the magnetization is switched. Therefore, it is very important the time of any measurement should not influence the magnetization switching. E.g. the measurement time should substantially shorter than the the magnetization switching time. The second reason of a systematical error is the statistical nature of the magnetization switching. The

How it is possible to measure the retention time of several billion years?

The retention time is the magnetization switching time without any external magnetic field and it can be very long. However, under external magnetic field the switching time exponentially decreases with magnitude of the field. The measurements are done under external magnetic field, at which the measurement of the magnetization switching time is convenient.

(measurement method 3): Switching time

Sample: Volt54A Ta(2.5 nm):FeB(1.1 nm)	Sample: Volt59A Ta(8 nm):FeB(0.9 nm)	Sample: Volt40 Ta(2 nm):FeB(1.3 nm)

H_c=31.6 G; domain size=68.5; retention time 7.4 hours	H_c=324 G; domain size=44.4; retention time 1,000,000 billion years
device: L68	device: L35	device: R71

click on image to enlarge it

Calculation Example 1 (left graph) Volt54A Ta(2.5 nm):FeB(1.1 nm)

Linear fit: 4.43-0.14·H

coercive field H_c=4.43/0.14=31.6 G

size of nucleation domain=sqrt(51717·0.14/1.4/1.1)=68.5 nm

retention time τ_ret=10^4.43sec=7.4 hours

parameter Δ =0.5· 0.14·2.5·1000=174

M=1.4 T; H_ani=2.5 kG; FeB thickness=1.1 nm;

nanomagnet size: 3 μm x 3 μm

Calculation Example 2 (center graph) Volt59A L68 Ta(8 nm):FeB(0.9 nm) (device:L35)

Linear fit: 26.224-0.07·H

coercive field H_c=26.224/0.07=367.8 G

size of nucleation domain=sqrt(51717·0.07/1.4/0.9)=54.1 nm

retention time τ_ret=10^26.2sec=3 10⁹ billion years

parameter Δ =0.5· 0.07·7.5·1000=267

M=1.4 T; H_ani=7.5 kG; FeB thickness=0.9 nm;

nanomagnet size: 3 μm x 3 μm

Calculation Example 3 (right graph) Volt40 Ta(2 nm):FeB(1.3 nm) (device:R71)

Linear fit: 22.5-0.07·H

coercive field H_c=22.5/0.07=324 G

size of nucleation domain=sqrt(51717·0.07/1.4/1.3)=44.4 nm

retention time τ_ret=10^22.5sec=10¹⁵ years=1,000,000 billion years

parameter Δ =0.5·0.07·4.4·1000=152

M=1.4 T; H_ani=4.4 kG; FeB thickness=1.3 nm;

nanomagnet size: 3 μm x 3 μm

(interesting fact) A slight change of nanomagnet structure or nanomagnet fabrication conditions can change the retention time from a hour to many many billions years (compare Volt54A with Volt40 and Volt59A)

Samples Volt59A, Volt40 and Volt54A are very similar. Why their magnetic properties are very different?

Reason 1 (minor): thickness of FeB FeB of Volt59A is slightly thicker than FeB of Volt54A . As a result, the contribution of the bulk of FeB becomes larger and the film becomes softer.

(note) the bulk of FeB forces the magnetization M into in- plane direction, the interface of FeB forces M into the perpendicular- to- plane direction. As a result, the PMA energy is large in thinner FeB film than in a thicker film.

Reason 2 (major): roughness of FeB interface The Ta layer is substantially thicker in Volt59A than in Volt54A . The thicker Ta layer makes smoother the FeB interface and therefore enhances the PMA

(note) PMA in FeB is induced by its interface. The PMA is larger when the FeB interface is smoother. The PMA is weaker when the FeB interface is rougher.

Reason 1 ;+ Reason 2 leads to the difference in PMA energy between samples. The PMA energy of Volt59A (H_ani=7.5 kG) is 1.7 times large than that of Volt40 (H_ani=4.4 kG) and 3 times larger that of Volt54A (H_ani=2.5 kG)

Reason 3 (major): unknown origin ?????

The huge difference in retention time between Volt54A ( τ_ret=7.4 hours) and Volt40 (τ_ret=10¹⁵ years), Volt59A (τ_ret=3 10¹⁸ years) cannot be explained by 1.8/3 times difference in the PMA energy.

Mechanism which makes such a huge difference in τ_ret between Volt54A and Volt40 is still a puzzle

Measurement of Voltage- Controlled Magnetic Anisotropy (VCMA effect)

Voltage- Controlled Magnetic Anisotropy (VCMA) effect
Dependence of magnetic properties on gate voltage

Magnetic properties of nanomagnet (FeB, shown in grey) are changed when a gate voltage is applied at a metal- isolator interface at the top of the nanomagnet. The source battery provides the bias current through the metallic nanowire and the nanomagnet. The voltmeter measured the Hall voltage, which is created perpendicularly to the bias current. The gate voltage is applied between the top of nanomagnet and the nanowire. Because of thick (~ 10 nm) gate isolator (MgO), the gate voltage does not induce any electrical current. The gate modulation does not change the temperature of the nanomagnet. It is the main merit of the modulation of the magnetic properties of nanomagnet by a gate voltage. The effect, which describes the dependence of the magnetic properties on the gate voltage, is called the Voltage- Controlled Magnetic Anisotropy (VCMA). See details here.
Ferromagnetic metal (FeB) is shown in grey. Non- magnetic metal (Ta) is shown in yellow color. Non-conductive isolator (SiO2) is shown in green. The used width of nanowire is between 50 nm and 3000 nm. The used length of nanomagnet is between 30 nm and 3000 nm. Due to the nano size of the FeB, its magnetization is always in single- domain state (parallel over whole volume). Therefore, the nano- sized FeB is called a nanomagnet. The magnetization of nanomagnet (FeB) is perpendicular to plane and is shown as green ball with red arrow. External magnetic field (red arrow) is applied either perpendicularly- to- plane (as shown) or in- plane.
click on image to enlarge it

(main idea): Dependence of magnetic parameters of a nanomagnet on magnitude of current j is measured. Since the gate voltage does not cause any electrical current, there is no influence of heating for this measurement.

All samples show the same dependence on the gate voltage. All magnetic parameters increased

Temperature dependence of magnetic parameters

(main idea): Dependence of magnetic parameters of a nanomagnet on magnitude of current j is measured. The heating and therefore the sample temperature is proportional to current square j².

dependence of magnetic parameters on temperature (~j²)

Relative change of Hall angle vs current	Dependence of anisotropy field H_anis on current	Dependence of coercive field H_c on current j

Sample Volt40 R21	Sample Volt40 R73	Sample Volt50 ud10

All magnetic parameters depends on current j as A · j² +B · j, where parameter A describes temperature dependence and parameter B describes dependence on polarity of j (SOT effect)

note: heating and therefore the sample temperature is proportional to j².

click on image to enlarge it

Measurement of Spin- orbit torque (SOT effect)

Spin-orbit torque (SOT) effect
dependence of magnetic properties on polarity of bias current

Magnetic properties of nanomagnet are changed when the value of bias is changed. The source battery provides the bias current through the metallic nanowire and the nanomagnet. The voltmeter measured the Hall voltage, which is created perpendicularly to the bias current. Since the used current density is relatively large ~ 50 mA/um2 (otherwise the Hall voltage is to small to detect), the temperature of the nanomagnet is changed when the magnitude of the current change. Additionally, the magnetic properties of the nanomagnet depend on the polarity of the current. This effect is called Spin- Orbit Torque (SOT). (See details here)
Ferromagnetic metal (FeB) is shown in grey. Non- magnetic metal (Ta) is shown in yellow color. Non-conductive isolator (SiO2) is shown in green. The used width of nanowire is between 50 nm and 3000 nm. The used length of nanomagnet is between 30 nm and 3000 nm. Due to the nano size of the FeB, its magnetization is always in single- domain state (parallel over whole volume). Therefore, the nano- sized FeB is called a nanomagnet. The magnetization of nanomagnet (FeB) is perpendicular to plane and is shown as green ball with red arrow. External magnetic field (red arrow) is applied either perpendicularly- to- plane (as shown) or in- plane.
click on image to enlarge it

(main idea): Dependence of magnetic parameters of a nanomagnet on polarity of current j is measured. In order to avoid the influence of heating due to the current, the same magnetic parameters is measured for two opposite currents. The difference of measured parameters ids due to the SOT effect.

Measurement in gate and gap regions

Measurement method: in gate and gap regions


a nanowire with two pairs of Hall probes. The Hall voltage is measured in region of nanomagnet ( unetched region at back of the nanowire), which is called the gate region. Simultaneously, the Hall voltage is measured in etched region, which is called the gap region.	SEM image (top view) of nanowire with two Hall probes.

(note): distance between gate and gap probes is 15 μm in all samples (EB or stepper- made)

click on image to enlarge it

(note) Thickness of ferromagnetic FeB layer is only 1 nm. It is hard to stop at a precise designed etched thickness.

(note) Etched materials were monitored during etching. Sensitivity of monitoring of Mg is high. Sensitivity of monitoring of Si,Fe,B,O2 is very low, because of chamber contamination by these elements. Sensitivity of monitoring of Ta is moderate/ low.

(note) It is critically important to monitor that Ta layer is not etched out.

Your pictures show that you are making electrical contact to Ta layer. Is it important?

It is much better to make the contact to FeB layer rather than to Ta layer. However, sometimes it is difficult (but possible) to stop inside FeB layer.

The reason why it is better to stop etching inside FeB is following. After the etching the hole for the contact and before the deposition of top Au contact the sample are exposed to air. As a result, its top surface is slightly oxidized making unwanted tunnel barrier for contact significantly increasing the contact resistance. If this unwanted tunnel barrier is thin and it is broken during measurement (e.g. under 1 V). On FeB the oxide is very thin and it has almost no influence on the contact resistance. The oxide on Ta is strong, hard to break and it has a substantial resistance. The worse case is the oxide on tungsten (W). It is very strong and highly resistant.

In all most- recent samples I can reliably stop etching for the contact inside FeB layer

Etching depth & coercive loop

Full etch


FeB layer is fully etched out. However, a weak hysteresis loop still can be observed in the gap region due to Fe diffusion into Ta layer during film growth and nano fabrication.	Sample: R21B Volt 40. There is a weak loop for the gap region

Half etched


FeB layer is only partially etched out. Thickness of FeB is different in the gate and gate regions.	Sample: Volt55 ud10. The hysteresis loop in gate region is higher than in gap region. The width (coercive field) in the gap region can be smaller ( often case) or large (rare case) than in gate region. Anisotropy field in gap region is smaller than in gate region.

Unetched


Only MgO layer is etched out. The etching is stopped at MgO/FeB interface. Thickness of FeB is the same in the gate and gate regions.	Sample: Volt50 free56. The height of the hysteresis loop is the same in the gate and gap regions. The coercive field is in gate and gap regions due to different size of the nucleation domain.

two nanomagnet on one naowire

design	Coercive loop

Samples, which name is ended with "C" (e.g. L24C), has two nanomagnet on one wire. Distance between nanomagnets is 10 um. The 1st nanomagnet nickname is "gate" and the 2nd nanomagnet nickname is "gap".	Sometime two identical nanomagnets, which are fabricated only 10 um from each other on the same nanowire, may show a differrent coercive loop.Sample: Volt40A L24C. Often the loops are the same.

Click on image to enlarge it

Samples

Volt 40A (Ret14) (Ta(2):FeB(1.3):MgO(5.1)/Ta(1)/Ru(5) )

All data is here

Magneto- static properties

Coercive field H_C	Anisotropy field H_anis	measured Hall angle α_{Hall, measured}

substantial difference of H_C from sample to sample (H_C= 100 Oe- 380 Oe)	H_anis is about 4.2 kG	For intrinsic Hall angle , the measured Hall angle α_{Hall, measured} should be multiplied per k_double=2.5385

Click on image to enlarge it

Conductivity: 0.023-0.029 S/m2

Anisotropy field H_anis=4.2 kGauss

Coercive field = 170 Oe-220 Oe;

Hall angle measured=290- 390 deg

Intrinsic Hall angle of FeB= 736- 990 mdeg;

Gap region etched: FeB is fully etched, stopped at FeB/ Ta interface

ample:( R21 gate) α_ISHE,0.5= 222 mdeg; α_AHE,0.5= 753 mdeg; α_OHE=0.2 mdeg/kG; H_p=13.6 kG;

range of H_p: 9.7 kG -21.6 mean H_p: 14.78 kG

magnetization- switching parameters:

retention time τ_ret: 10²¹ s

size of nucleation domain: 40 nm;

coercive field H_c: 310 Oe

parameter Δ : 120

(Volt 40) Spin- orbit torque

Spin-orbit torque. (SOT)

dependence of magnetic parameters on current and current polarity flowing through a nanomagnet

"Field- like torque".	"Damp- like torque".	Dependence of offset magnetic field H_off on perpendicularly applied magnetic field H.
Current- dependence of offset field dH_off/dj. Scan is along wire	Current- dependence of offset field ∂H_off/∂j. Scan is perpendicularly to wire

dH_off/dj= 0.15 G/(mA/μm²) and dH_off/dj= 0.35 G/(mA/μm²)	dH_off/dj= 0.15 G/(mA/μm²) . There are two exceptions

Dependence of AHE on polarity of current j	Dependence of H_C on polarity of current j	Dependence of offset magnetic field H_off on current j.

ΔAHE= (α_Hall(j)-α_Hall(-j))/2/α_Hall(j). All slopes are negative. There is a saturation at 25 mA/μm²	The change of H_C with reverse of polarity of current: ΔH_C= (H_C(j)-H_C(-j))/2. There are both negative and positive slopes	Dependence is linear. Slope is positive. Measurement is under perpendicular magnetic field H is + 0.8 kG. Scan is along wire.

Click on image to enlarge it

(Volt 40) Voltage controlled magnetic anisotropy (VCMA)

Voltage controlled magnetic anisotropy. (VCMA)

dependence of magnetic parameters on a gate voltage

Dependence of anisotropy field H_anis on gate voltage V	dependence of coercive field H_C on gate voltage	Dependence of Anomalous Hall effect on gate voltage	Change anisotropy field H_anis under gate voltage vs perpendicular magnetic field
	H_C is normalized as H_C(%)= (H_C(V)-H_C(V=-1V))/H_C(V)	Dependence of normalized Hall angle α_Hallis shown. α_Hall is normalized as α_Hall(%)= (α_Hall(V)-α_Hall(V=-1V))/α_Hall(V)

H_anis is linearly proportional to the gate voltage. Slope is negative.	Voltage dependence is unclear	Voltage dependence is unclear	∂H_anis/∂V ~ -0.03 kG/V. The change of H_anis is 30 G at gate voltage of 1 V or 0.6 %. Dependence on H_zis periodical.

Click on image to enlarge it

Volt 50B (Ta(3)/ FeB(1.1)/ MgO(7)/ W(1)/ Ru(5))

All data is here

Magneto- static properties

Coercive field H_C	Anisotropy field H_anis	measured Hall angle α_{Hall, measured}

H_C= 170 Oe-220 Oe	H_anis is about 5 kG.	For intrinsic Hall angle , the measured Hall angle α_{Hall, measured} should be multiplied per k_double=3.7273

Click on image to enlarge it

Conductivity: 0.039-0.62 S/m2

Anisotropy field H_anis=5kGauss

Coercive field = 170 Oe-220 Oe;

Hall angle measured=450- 800 deg

Intrinsic Hall angle of FeB= ;

Gap region etched: stopped at MgO/ FeB interface

sample:( free36 gate) α_ISHE,0.5= 213 mdeg; α_AHE,0.5= 1777 mdeg; α_OHE=0.2 mdeg/kG; H_p=9.72 kG;

magnetization- switching parameters:

retention time τ_ret: 10¹⁴ s

size of nucleation domain: 45 nm;

coercive field H_c: 200 Oe

parameter Δ : 150

(Volt 50B) Spin- orbit torque

Spin-orbit torque. (SOT)

dependence of magnetic parameters on current and current polarity flowing through a nanomagnet

"Field- like torque".	"Damp- like torque".	Dependence of offset magnetic field H_off on perpendicularly applied magnetic field H.
Current- dependence of offset field dH_off/dj. Scan is along wire	Current- dependence of offset field ∂H_off/∂j. Scan is perpendicularly to wire

dH_off/dj= 0.15 G/(mA/μm²) and dH_off/dj= 0.35 G/(mA/μm²)	dH_off/dj= 0.15 G/(mA/μm²)

Dependence of AHE on polarity of current j	Dependence of H_C on polarity of current j	Dependence of offset magnetic field H_off on current j.

ΔAHE= (α_Hall(j)-α_Hall(-j))/2/α_Hall(j). All slopes are negative. There is a saturation at 50 mA/μm²	The change of H_C with reverse of polarity of current: ΔH_C= (H_C(j)-H_C(-j))/2. There are both negative and positive slopes	Dependence is linear. Slope is positive. Measurement is under perpendicular magnetic field H is + 0.8 kG. Scan is along wire.

Click on image to enlarge it

Volt 53B Ta(2.5 nm)/FeBCo(x=0.3, 1 nm) / MgO(7 nm)/ Ta(1nm)/ Ru(5 nm))

All data is here

Magneto- static properties

Coercive field H_C	Anisotropy field H_anis	measured Hall angle α_{Hall, measured}

H_C= 200 Oe-330 Oe	H_anis is 2.2 kG- 6kG.	For intrinsic Hall angle α_{Hall, FeB}, the measured Hall angle α_{Hall, measured} should be multiplied per k_double=3.5

Click on image to enlarge it

Conductivity: 0.04-0.06 S/m2

Anisotropy field H_anis=2.2 kGauss-6 kGauss

Coercive field = 200 Oe-330 Oe;

Hall angle measured α_{Hall, measured} =290- 750 mdeg

Intrinsic Hall angle of FeB α_{Hall, FeB}= 1015 - 2625 mdeg;

Gap region etched: FeB is partially etched, stopped in middle of FeCoB

sample:( ud66) α_ISHE,0.5= 274 mdeg; α_AHE,0.5=2324 mdeg; α_OHE=0.2 mdeg/kG; H_p=5.84 kG;

(Volt 53B) Spin- orbit torque

Spin-orbit torque. (SOT)

dependence of magnetic parameters on current and current polarity flowing through a nanomagnet

"Field- like torque".	"Damp- like torque".	Dependence of offset magnetic field H_off on perpendicularly applied magnetic field H.
Current- dependence of offset field dH_off/dj. Scan is along wire	Current- dependence of offset field ∂H_off/∂j. Scan is perpendicularly to wire	"Field- like torque". Scan is along wire.

dH_off/dj= 0.5 G/(mA/μm²)	dH_off/dj= 0.4 G/(mA/μm²)

Dependence of AHE on polarity of current j	Dependence of H_C on polarity of current j	Dependence of offset magnetic field H_off on current j.

ΔAHE= (α_Hall(j)-α_Hall(-j))/2/α_Hall(j). There are both negative and positive slopes. There is a saturation at 25 mA/μm²	The change of H_C with reverse of polarity of current: ΔH_C= (H_C(j)-H_C(-j))/2. Large slopes are positive and small slopes are negative	Dependence is linear. Slope is positive. Measurement is under perpendicular magnetic field H is + 0.8 kG. Scan is along wire.

Click on image to enlarge it

(Volt 53B) Voltage controlled magnetic anisotropy (VCMA)

Voltage controlled magnetic anisotropy. (VCMA)

dependence of magnetic parameters on a gate voltage

Dependence of anisotropy field H_anis on gate voltage V	dependence of coercive field H_C on gate voltage	Dependence of Anomalous Hall effect on gate voltage	Change anisotropy field H_anis under gate voltage vs perpendicular magnetic field
	H_C is normalized as H_C(%)= (H_C(V)-H_C(V=-1V))/H_C(V)	Dependence of normalized Hall angle α_Hallis shown. α_Hall is normalized as α_Hall(%)= (α_Hall(V)-α_Hall(V=-1V))/α_Hall(V)

H_anis is linearly proportional to the gate voltage. Slope is negative.	Voltage dependence is unclear	Voltage dependence is unclear	∂H_anis/∂V ~ -0.1 kG/V. The change of H_anis is 100 G at gate voltage of 1 V or ~2.5 %. Dependence on H_zis periodical.

Click on image to enlarge it

Volt54A (Ret14) Ta(2.5 nm)/ FeB(1.1 nm)/ MgO(6 nm)/ Ta(1 nm)/ Ru(5 nm)

All data is here

Magneto- static properties

Coercive field H_C	Anisotropy field H_anis	measured Hall angle α_{Hall, measured}
too small to measure
H_C= 20 Oe-70 Oe	H_anis is 2.5 kG.	For intrinsic Hall angle α_{Hall, FeB}, the measured Hall angle α_{Hall, measured} should be multiplied per k_double=3.2727

Click on image to enlarge it

Conductivity: 0.055-0.06 S/m2

Anisotropy field H_anis=2.5 kGauss

Coercive field = 20 Oe-70 Oe;

Hall angle measured α_{Hall, measured} =320- 370 mdeg

Intrinsic Hall angle of FeB α_{Hall, FeB}= 1047 - 1211 mdeg;

Gap region etched: FeB is partially etched, stopped in middle of FeB

sample:( L70) α_ISHE,0.5= 351 mdeg; α_AHE,0.5= 695 mdeg; α_OHE=0.2 mdeg/kG; H_p=5.84 kG;

(Volt 54A) Spin- orbit torque

Spin-orbit torque. (SOT)

dependence of magnetic parameters on current and current polarity flowing through a nanomagnet

"Field- like torque".	"Damp- like torque".	Dependence of offset magnetic field H_off on perpendicularly applied magnetic field H.
Current- dependence of offset field dH_off/dj. Scan is along wire	Current- dependence of offset field ∂H_off/∂j. Scan is perpendicularly to wire

dH_off/dj= 0.2 G/(mA/μm²)	dH_off/dj= 0.5 G/(mA/μm²)

Dependence of AHE on polarity of current j	Dependence of H_C on polarity of current j	Dependence of offset magnetic field H_off on current j.
	no data
ΔAHE= (α_Hall(j)-α_Hall(-j))/2/α_Hall(j). All slopes are negative. There is a saturation at 50 mA/μm²		Dependence is linear. Slope is positive. Measurement is under perpendicular magnetic field H is + 0.8 kG. Scan is along wire.

Click on image to enlarge it

(Volt 54B) Voltage controlled magnetic anisotropy (VCMA)

Voltage controlled magnetic anisotropy. (VCMA)

dependence of magnetic parameters on a gate voltage

Dependence of anisotropy field H_anis on gate voltage V	Dependence of Anomalous Hall effect on gate voltage	Change anisotropy field H_anis under gate voltage vs perpendicular magnetic field
	H_C is normalized as H_C(%)= (H_C(V)-H_C(V=-1V))/H_C(V)	Dependence of normalized Hall angle α_Hallis shown. α_Hall is normalized as α_Hall(%)= (α_Hall(V)-α_Hall(V=-1V))/α_Hall(V)

H_anis is linearly proportional to the gate voltage. Slope is negative.	Slope is negative and non-linear	∂H_anis/∂V ~ -0.12 kG/V. The change of H_anis is 120 G at gate voltage of 1 V or 5.45 %. Dependence on H_zis periodical and period is large

Click on image to enlarge it

Volt54B Ta(2.5 nm)/ FeB(1.1 nm)/ MgO(6 nm)/ Ta(1 nm)/ Ru(5 nm)

All data is here

Magneto- static properties

Coercive field H_C	Anisotropy field H_anis	measured Hall angle α_{Hall, measured}
too small to measure
H_C= 20 Oe-70 Oe	H_anis is 2.5 kG.	For intrinsic Hall angle α_{Hall, FeB}, the measured Hall angle α_{Hall, measured} should be multiplied per k_double=3.2727

Click on image to enlarge it

Conductivity: 0.037-0.06 S/m2

Anisotropy field H_anis=2 kGauss

Coercive field = 5 Oe-50 Oe;

Hall angle measured α_{Hall, measured} =350-400 mdeg

Intrinsic Hall angle of FeB α_{Hall, FeB}= 1145 - 1309 mdeg;

Gap region etched: FeB is partially etched, stopped in middle of FeB

sample:( free28 gate) α_ISHE,0.5= 551 mdeg; α_AHE,0.5= 675 mdeg; α_OHE=0.2 mdeg/kG; H_p=3.954 kG;

(Volt 54B) Spin- orbit torque

Spin-orbit torque. (SOT)

dependence of magnetic parameters on current and current polarity flowing through a nanomagnet

"Field- like torque".	"Damp- like torque".	Dependence of offset magnetic field H_off on perpendicularly applied magnetic field H.
Current- dependence of offset field dH_off/dj. Scan is along wire	Current- dependence of offset field ∂H_off/∂j. Scan is perpendicularly to wire

dH_off/dj= 0.6 G/(mA/μm²)	dH_off/dj= 1 G/(mA/μm²) . Peak at 1.5 kG.

Dependence of AHE on polarity of current j	Dependence of H_C on polarity of current j	Dependence of offset magnetic field H_off on current j.
	no data
ΔAHE= (α_Hall(j)-α_Hall(-j))/2/α_Hall(j). There are both negative and positive slopes. There is a saturation at 25 mA/μm²		Dependence is linear. Slope is positive. Saturation at positive j? Measurement is under perpendicular magnetic field H is + 0.8 kG. Scan is along wire.

Click on image to enlarge it

(Volt 54B) Voltage controlled magnetic anisotropy (VCMA)

Voltage controlled magnetic anisotropy. (VCMA)

dependence of magnetic parameters on a gate voltage

Dependence of anisotropy field H_anis on gate voltage V	Dependence of Anomalous Hall effect on gate voltage	Change anisotropy field H_anis under gate voltage vs perpendicular magnetic field
	Dependence of normalized Hall angle α_Hallis shown. α_Hall is normalized as α_Hall(%)= (α_Hall(V)-α_Hall(V=-1V))/α_Hall(V)
		no data
H_anis is linearly proportional to the gate voltage. Slope is negative.	AHE is linearly proportional to the gate voltage. Slope is negative.

Click on image to enlarge it

Volt 55 Ta(5 nm)/ FeB(0.9 nm)/ MgO(6 nm)/ Ta(1 nm)/ Ru(5 nm)

All data is here

Magneto- static properties

Coercive field H_C	Anisotropy field H_anis	measured Hall angle α_{Hall, measured}

H_C= 200 Oe-330 Oe	H_anis is 2.2 kG- 6kG.	For intrinsic Hall angle α_{Hall, FeB}, the measured Hall angle α_{Hall, measured} should be multiplied per k_double=6.5556

Click on image to enlarge it

Conductivity: 0.028-0.038 S/m2

Anisotropy field H_anis=4 kGauss-11 kGauss

Coercive field = 150 Oe-225 Oe; (a few: 400 Oe,90 Oe)

Hall angle measured α_{Hall, measured} =200- 650 mdeg

Intrinsic Hall angle of FeB α_{Hall, FeB}= 1311 - 4261 mdeg;;

Gap region etched: FeB is fully (partiality) etched, stopped at Ta/FeB interface (in middle of FeCoB)

sample:(ud40) α_ISHE,0.5= 323.8 mdeg; α_AHE,0.5= 1141 mdeg; α_OHE=0.2 mdeg/kG; H_p=7.25 kG;

(Volt 55) Spin- orbit torque

Spin-orbit torque. (SOT)

dependence of magnetic parameters on current and current polarity flowing through a nanomagnet

"Field- like torque".	"Damp- like torque".	Dependence of offset magnetic field H_off on perpendicularly applied magnetic field H.
Current- dependence of offset field dH_off/dj. Scan is along wire	Current- dependence of offset field ∂H_off/∂j. Scan is perpendicularly to wire	Data of Sample free 77 gate

top data: dH_off/dj= 0.8 G/(mA/μm²) and average data: dH_off/dj= 0.4 mA/μm²	top data: dH_off/dj= 0.9 G/(mA/μm²) . average data: dH_off/dj= 0.4 G/(mA/μm²) .

Dependence of AHE on polarity of current j	Dependence of H_C on polarity of current j	Dependence of offset magnetic field H_off on current j.

ΔAHE= (α_Hall(j)-α_Hall(-j))/2/α_Hall(j). All slopes are negative. There is a saturation at 25 mA/μm²	The change of H_C with reverse of polarity of current: ΔH_C= (H_C(j)-H_C(-j))/2. There are both negative and positive slopes	Dependence is linear. Slope is positive. Measurement is under perpendicular magnetic field H is + 0.8 kG. Scan is along wire. Data of Sample free 77 gate.

Click on image to enlarge it

(Volt 55) Voltage controlled magnetic anisotropy (VCMA)

Voltage controlled magnetic anisotropy. (VCMA)

dependence of magnetic parameters on a gate voltage

Dependence of anisotropy field H_anis on gate voltage V	dependence of coercive field H_C on gate voltage	Dependence of Anomalous Hall effect on gate voltage	Change anisotropy field H_anis under gate voltage vs perpendicular magnetic field
	H_C is normalized as H_C(%)= (H_C(V)-H_C(V=-1V))/H_C(V)	Dependence of normalized Hall angle α_Hallis shown. α_Hall is normalized as α_Hall(%)= (α_Hall(V)-α_Hall(V=-1V))/α_Hall(V)
no data
	H_c is linearly proportional to the gate voltage. Slope is negative.	Voltage dependence is unclear	∂H_anis/∂V ~ -0.2 kG/V. The change of H_anis is 200 G at gate voltage of 1 V or 10 %. Dependence on H_zis periodical.

Click on image to enlarge it

Volt 57A (Ret14): Ta(5 nm)/ FeCoB( x=0.5 1.1 nm)/ MgO(7 nm)/ Ta(1 nm)/ Ru(5 nm)

All data is here

Magneto- static properties

Coercive field H_C	Anisotropy field H_anis	measured Hall angle α_{Hall, measured}

H_C= 200 Oe-330 Oe	H_anis is 2.2 kG- 6kG.	For intrinsic Hall angle α_{Hall, FeB}, the measured Hall angle α_{Hall, measured} should be multiplied per k_double=5.5455

Click on image to enlarge it

Conductivity: 0.044-0.055 S/m2

Anisotropy field H_anis=4.8 kGauss

Coercive field = 200 Oe-330 Oe;

Hall angle measured α_{Hall, measured} =175- 235 mdeg

Intrinsic Hall angle of FeB α_{Hall, FeB}= 970- 1303 mdeg;

Gap region etched: FeB is fully etched, stopped at Ta/FeCoB interface

sample:( L66) α_ISHE,0.5= 241 mdeg; α_AHE,0.5= 930 mdeg; α_OHE=0.2 mdeg/kG; H_p=5.5 kG;

(Volt 57A) Spin- orbit torque

Spin-orbit torque. (SOT)

dependence of magnetic parameters on current and current polarity flowing through a nanomagnet

"Field- like torque".	"Damp- like torque".	Dependence of offset magnetic field H_off on perpendicularly applied magnetic field H.
Current- dependence of offset field dH_off/dj. Scan is along wire	Current- dependence of offset field ∂H_off/∂j. Scan is perpendicularly to wire	Data of Sample L70

most data: dH_off/dj= 0.3 G/(mA/μm²) and one data: dH_off/dj= 0.55 G/(mA/μm²)	dH_off/dj= 0.2 G/(mA/μm²) .

Dependence of AHE on polarity of current j	Dependence of H_C on polarity of current j	Dependence of offset magnetic field H_off on current j.

ΔAHE= (α_Hall(j)-α_Hall(-j))/2/α_Hall(j). All slopes are negative. There is a saturation at 25 mA/μm²	The change of H_C with reverse of polarity of current: ΔH_C= (H_C(j)-H_C(-j))/2. There are both negative and positive slopes	Dependence is linear. Slope is positive. Measurement is under perpendicular magnetic field H is + 0.8 kG. Scan is along wire. Data of Sample L70

Click on image to enlarge it

(Volt 57A) Voltage controlled magnetic anisotropy (VCMA)

Voltage controlled magnetic anisotropy. (VCMA)

dependence of magnetic parameters on a gate voltage

Dependence of anisotropy field H_anis on gate voltage V	dependence of coercive field H_C on gate voltage	Dependence of Anomalous Hall effect on gate voltage	Change anisotropy field H_anis under gate voltage vs perpendicular magnetic field
	H_C is normalized as H_C(%)= (H_C(V)-H_C(V=-1V))/H_C(V)	Dependence of normalized Hall angle α_Hallis shown. α_Hall is normalized as α_Hall(%)= (α_Hall(V)-α_Hall(V=-1V))/α_Hall(V)

H_anis is linearly proportional to the gate voltage. Slope is negative. There is a saturation at H_gate> + 1.5 V	H_C is linearly proportional to the gate voltage. Slope is negative. There is a saturation at H_gate> + 1.5 V	AHE is linearly proportional to the gate voltage. Slope is negative. There is a saturation at H_gate> + 1.5 V	∂H_anis/∂V ~ -0.14 kG/V. The change of H_anis is 140 G at gate voltage of 1 V or 3.5 %. Dependence on H_zis periodical.

Click on image to enlarge it

Volt 57B (Ret14): Ta(5 nm)/ FeCoB( x=0.5 1.1 nm)/ MgO(7 nm)/ Ta(1 nm)/ Ru(5 nm)

All data is here

Magneto- static properties

Coercive field H_C	Anisotropy field H_anis	measured Hall angle α_{Hall, measured}

H_C= 200 Oe-330 Oe	H_anis is 2.2 kG- 6kG.	For intrinsic Hall angle α_{Hall, FeB}, the measured Hall angle α_{Hall, measured} should be multiplied per k_double=5.5455

Click on image to enlarge it

Conductivity: 0.02-0.027 S/m2

Anisotropy field H_anis=5 kGauss

Coercive field = 620 Oe-740 Oe;

Hall angle measured α_{Hall, measured} =110- 150 deg

Intrinsic Hall angle of FeB α_{Hall, FeB}= 610- 831 mdeg;;

Gap region etched: FeB is partially etched, stopped in middle of FeCoB

sample:( L20) α_ISHE,0.5= 65 mdeg; α_AHE,0.5= 594 mdeg; α_OHE=0.2 mdeg/kG; H_p=8.9 kG;

(Volt 57B) Spin- orbit torque

Spin-orbit torque. (SOT)

dependence of magnetic parameters on current and current polarity flowing through a nanomagnet

"Field- like torque".	"Damp- like torque".	Dependence of offset magnetic field H_off on perpendicularly applied magnetic field H.
Current- dependence of offset field dH_off/dj. Scan is along wire	Current- dependence of offset field ∂H_off/∂j. Scan is perpendicularly to wire	Data of Sample R62.

dH_off/dj= 0.3 G/(mA/μm²)	dH_off/dj= 0.15 G/(mA/μm²)

Dependence of AHE on polarity of current j	Dependence of H_C on polarity of current j	Dependence of offset magnetic field H_off on current j.

ΔAHE= (α_Hall(j)-α_Hall(-j))/2/α_Hall(j). All slopes are positive. There is no saturation	The change of H_C with reverse of polarity of current: ΔH_C= (H_C(j)-H_C(-j))/2. All slopes are positive	Dependence is linear. Slope is positive. Measurement is under perpendicular magnetic field H is + 0.8 kG. Scan is along wire. Data of Sample R62.

Click on image to enlarge it

(Volt 57B) Voltage controlled magnetic anisotropy (VCMA)

Voltage controlled magnetic anisotropy. (VCMA)

dependence of magnetic parameters on a gate voltage

Dependence of anisotropy field H_anis on gate voltage V	dependence of coercive field H_C on gate voltage	Dependence of Anomalous Hall effect on gate voltage	Change anisotropy field H_anis under gate voltage vs perpendicular magnetic field
	H_C is normalized as H_C(%)= (H_C(V)-H_C(V=-1V))/H_C(V)	Dependence of normalized Hall angle α_Hallis shown. α_Hall is normalized as α_Hall(%)= (α_Hall(V)-α_Hall(V=-1V))/α_Hall(V)

H_anis is linearly proportional to the gate voltage. Slope is negative. There is a weak saturation at H_gate> + 1.5 V	H_C is linearly proportional to the gate voltage. Slope is negative. There is a saturation at H_gate> + 1.5 V	AHE is linearly proportional to the gate voltage. Slope is negative. There is a saturation at H_gate> + 1.5 V	∂H_anis/∂V ~ -0.03 kG/V. The change of H_anis is 30 G at gate voltage of 1 V or 0.6 %. Dependence on H_zis periodical.

Click on image to enlarge it

Volt 58A (Ret14): Ta(5 nm)/ (FeCo 1 nm, x=0.3)/ MgO(7 nm)/ Ta(1 nm)/ Ru(5 nm)

All data is here

Magneto- static properties

Coercive field H_C	Anisotropy field H_anis	measured Hall angle α_{Hall, measured}

H_C= 200 Oe-330 Oe	H_anis is 2.2 kG- 6kG.	For intrinsic Hall angle α_{Hall, FeB}, the measured Hall angle α_{Hall, measured} should be multiplied per k_double=6

Click on image to enlarge it

Conductivity: 0.048-0.051 S/m2

Anisotropy field H_anis=6.5 kGauss-8.5 kGauss

Coercive field = 200 Oe-330 Oe;

Hall angle measured α_{Hall, measured} =360- 470 mdeg

Intrinsic Hall angle of FeB α_{Hall, FeB}=2160- 2820 mdeg;

Gap region etched: FeCoB is partially etched, stopped in middle of FeCoB

sample:( R41 gate) α_ISHE,0.5= 377 mdeg; α_AHE,0.5= 1497 mdeg; α_OHE=0.2 mdeg/kG; H_p=8.8 kG;

(Volt 58A) Spin- orbit torque

Spin-orbit torque. (SOT)

dependence of magnetic parameters on current and current polarity flowing through a nanomagnet

"Field- like torque".	"Damp- like torque".	Dependence of offset magnetic field H_off on perpendicularly applied magnetic field H.
Current- dependence of offset field dH_off/dj. Scan is along wire	Current- dependence of offset field ∂H_off/∂j. Scan is perpendicularly to wire	Data of Sample R62C

dH_off/dj= 0.15 G/(mA/μm²) and dH_off/dj= 0.35 G/(mA/μm²)	dH_off/dj= 0.15 G/(mA/μm²) .

Dependence of AHE on polarity of current j	Dependence of H_C on polarity of current j	Dependence of offset magnetic field H_off on current j.

ΔAHE= (α_Hall(j)-α_Hall(-j))/2/α_Hall(j). All slopes are negative. There is a saturation at 40 mA/μm²	The change of H_C with reverse of polarity of current: ΔH_C= (H_C(j)-H_C(-j))/2. There are both negative and positive slopes	Dependence is linear. Slope is positive. Measurement is under perpendicular magnetic field H is + 0.8 kG. Scan is along wire. Data of Sample R62C

Click on image to enlarge it

(Volt 58A) Voltage controlled magnetic anisotropy (VCMA)

Voltage controlled magnetic anisotropy. (VCMA)

dependence of magnetic parameters on a gate voltage

Dependence of anisotropy field H_anis on gate voltage V	dependence of coercive field H_C on gate voltage	Dependence of Anomalous Hall effect on gate voltage	Change anisotropy field H_anis under gate voltage vs perpendicular magnetic field
	H_C is normalized as H_C(%)= (H_C(V)-H_C(V=-1V))/H_C(V)	Dependence of normalized Hall angle α_Hallis shown. α_Hall is normalized as α_Hall(%)= (α_Hall(V)-α_Hall(V=-1V))/α_Hall(V)

H_anis is linearly proportional to the gate voltage. Slope is negative. There is a saturation at H_gate< -1 V	H_C is linearly proportional to the gate voltage. Slope is negative. There is a saturation at both H_gate> + 1 V and H_gate< -1 V	AHE is linearly proportional to the gate voltage. Slope is negative. There is a saturation at H_gate> + 1 V	∂H_anis/∂V ~ -0.12 kG/V. The change of H_anis is 120 G at gate voltage of 1 V or 1.6 %. Dependence on H_zis periodical.

Click on image to enlarge it

Volt 59A (Ret14): Ta(8 nm)/ FeB(0.9 nm)/ MgO(7.1 nm)/ Ta(1 nm)/ Ru(5 nm)

All data is here

Magneto- static properties

Coercive field H_C	Anisotropy field H_anis	measured Hall angle α_{Hall, measured}

H_C= 200 Oe-330 Oe	H_anis is 2.2 kG- 6kG.	For intrinsic Hall angle α_{Hall, FeB}, the measured Hall angle α_{Hall, measured} should be multiplied per k_double=9.8889

Click on image to enlarge it

Conductivity: 0.048-0.052 S/m2

Anisotropy field H_anis=8 kGauss-11 kGauss

Coercive field = 280 Oe-550 Oe;

Hall angle measured α_{Hall, measured} =125- 145 mdeg

Intrinsic Hall angle of FeB α_{Hall, FeB}= 1236 -1434 mdeg;

Gap region etched: FeB is partially etched, stopped in middle of FeCoB

sample:( L19) α_ISHE,0.5= 270.3 mdeg; α_AHE,0.5= 1110 mdeg; α_OHE=0.2 mdeg/kG; H_p=8.95 kG;

(Volt 59A) Spin- orbit torque

Spin-orbit torque. (SOT)

dependence of magnetic parameters on current and current polarity flowing through a nanomagnet

"Field- like torque".	"Damp- like torque".	Dependence of offset magnetic field H_off on perpendicularly applied magnetic field H.
Current- dependence of offset field dH_off/dj. Scan is along wire	Current- dependence of offset field ∂H_off/∂j. Scan is perpendicularly to wire	Data of Sample R71.

top data: dH_off/dj= 0.4 G/(mA/μm²) and dH_off/dj= 0.3 G/(mA/μm²)	dH_off/dj= 0.45 G/(mA/μm²) .

Dependence of AHE on polarity of current j	Dependence of H_C on polarity of current j	Dependence of offset magnetic field H_off on current j.

ΔAHE= (α_Hall(j)-α_Hall(-j))/2/α_Hall(j). All slopes are negative. There is one exception There is a saturation at 25 mA/μm²	The change of H_C with reverse of polarity of current: ΔH_C= (H_C(j)-H_C(-j))/2.. There are both negative and positive slopes	Dependence is linear. Slope is positive. Measurement is under perpendicular magnetic field H is + 0.8 kG. Scan is along wire. Data of Sample R71.

Click on image to enlarge it

(Volt 59A) Voltage controlled magnetic anisotropy (VCMA)

Voltage controlled magnetic anisotropy. (VCMA)

dependence of magnetic parameters on a gate voltage

Dependence of anisotropy field H_anis on gate voltage V	dependence of coercive field H_C on gate voltage	Dependence of Anomalous Hall effect on gate voltage	Change anisotropy field H_anis under gate voltage vs perpendicular magnetic field
	H_C is normalized as H_C(%)= (H_C(V)-H_C(V=-1V))/H_C(V)	Dependence of normalized Hall angle α_Hallis shown. α_Hall is normalized as α_Hall(%)= (α_Hall(V)-α_Hall(V=-1V))/α_Hall(V)

H_anis is linearly proportional to the gate voltage. Slope is negative. (Slope is negative. There is a saturation at H_gate> + 1 V )???	Voltage dependence is unclear	Voltage dependence is unclear. (Slope is negative. There is a saturation at H_gate> + 1 V )???	Voltage dependence is unclear

Click on image to enlarge it

Volt59B: Ta(8 nm)/ FeB(0.9 nm)/ MgO(7.1 nm)/ Ta(1 nm)/ Ru(5 nm)

All data is here

Magneto- static properties

Coercive field H_C	Anisotropy field H_anis	measured Hall angle α_{Hall, measured}

H_C= 200 Oe-330 Oe	H_anis is 2.2 kG- 6kG.	For intrinsic Hall angle α_{Hall, FeB}, the measured Hall angle α_{Hall, measured} should be multiplied per k_double=9.8889

Click on image to enlarge it

Conductivity: 0.02-0.054 S/m2

Anisotropy field H_anis=6 kGauss-9 kGauss

Coercive field = 220 Oe-290 Oe;

Hall angle measured α_{Hall, measured} =120- 240 mdeg

Intrinsic Hall angle of FeB α_{Hall, FeB}= 1186- 2373 mdeg;;

Gap region etched: FeB is not etched, stopped at MgO/FeB interface

sample:( free71gate) α_ISHE,0.5= 141.25 mdeg; α_AHE,0.5= 1636.1 mdeg; α_OHE=0.2 mdeg/kG; H_p=10.46 kG;

(Volt 59B) Spin- orbit torque

Spin-orbit torque. (SOT)

dependence of magnetic parameters on current and current polarity flowing through a nanomagnet

"Field- like torque".	"Damp- like torque".	Dependence of offset magnetic field H_off on perpendicularly applied magnetic field H.
Current- dependence of offset field dH_off/dj. Scan is along wire	Current- dependence of offset field ∂H_off/∂j. Scan is perpendicularly to wire	Data of Sample free29 gate

max data dH_off/dj= 0.4 G/(mA/μm²) and average data dH_off/dj= 0.1 G/(mA/μm²)	dH_off/dj= 0.15 G/(mA/μm²) .

Dependence of AHE on polarity of current j	Dependence of H_C on polarity of current j	Dependence of offset magnetic field H_off on current j.

ΔAHE= (α_Hall(j)-α_Hall(-j))/2/α_Hall(j). All slopes are negative. There is a saturation at 25 mA/μm²	The change of H_C with reverse of polarity of current: ΔH_C= (H_C(j)-H_C(-j))/2. There are both negative and positive slopes. The dependence is weak.	Dependence is linear. Slope is positive. Measurement is under perpendicular magnetic field H is + 0.8 kG. Scan is along wire. Data of Sample free29 gate

Click on image to enlarge it

(Volt 59B) Voltage controlled magnetic anisotropy (VCMA)

no data

I am strongly against a fake and "highlight" research

Dr. Vadym Zayets

v.zayets(at)gmail.com

more Chapters on this topic:

more Chapters on this topic:

Spin and Charge Transport

Abstract:

Exploring a very high precision of the developed measurement methods, the dependence of the magnetic parameters on gate voltage (the voltage- controlled magnetic anisotropy (VCMA) effect) and the current (spin- orbit torque (SOT) effect) was precisely measured and studied.

Single-layer nanomagnet. Optical lithography only.

nanomagnet size 3um x 3 um

click on wafer name to see more detailed data

Single-layer nanomagnet. Electron lithography.

width of nanomagnet is 100 nm or 200 nm or 400 nm or 1000 nm or 2000 nm

length of nanomagnet is 50 nm or 100 nm or 200 nm or 400 nm or 1000 nm or 2000 nm

Multi-layer nanomagnet. .

nanomagnet size 3um x 3 um

click on wafer name to see more detailed data

Content

click on the chapter for the shortcut

Measurement method: Hall effect

Modulation methods: gate voltage or bias current

Modulation by gate voltage

Modulation by bias current

(11) Questions & Answers

Measurement Data of all nanomagnets

Data of All nanomagnets

PMA & strength of the spin-orbit interaction

Measurement methods

All measurement method have been developed by me in 2018-2020. The features of all methods are a high- repeatability, high-reproducibility and very high measurement precision. I do my best to avoid and eliminate any possible systematical error.

Measurement methods 1 & 3

Measurement method 2

Hall angle αHall vs. external perpendicular magnetic field

1st derivative

2nd derivative

Is it possible to detect the existence of the static domains from this measurements?

Hall angle αHall vs. external perpendicular magnetic field

1st derivative

2nd derivative

(note 2): There are sample where it is not the case (See details of each sample)

Hall angle αHall vs. external perpendicular magnetic field

1st derivative

2nd derivative

(note 2): There are sample where it is not the case (See details of each sample)

Note: Lines for different current perfectly coincides to each other for 0 and 1st derivatives

Hall angle α_Hall vs. external perpendicular magnetic field

Hall angle α_Hall vs. external perpendicular magnetic field

Hall angle α_Hall vs. external perpendicular magnetic field