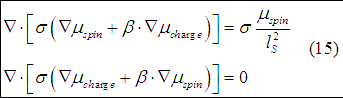Spin and Carge Transport Equations
Spin and Charge Transport. Classical model of the spin-up/spin-down band.
It is important!!!! All data on this page are calculated based on the model of the spin-up/spin-down bands. The model of the spin-up/spin-down bands ignores the fact that the spin is often rotated after spin-independent scatterings(See here). Therefore, some predictions based on this model may be incorrect and differ from a experimental observation. 
For the modified model, which includes all above-mentioned facts, click here or here
The same content can be foundin 
V. Zayets Phys. Rev. B 86, 174415 (2012) (clich here to download pdf);or http://arxiv.org/abs/1205.1278
Abstract:
The charge and spin transport equations is derived from the spin and charge conservation laws.
Introduction
For the last 20 years, spin transport in solids has been successfully described by the Valet-Fert spin diffusion equation [Ref.]. The Valet-Fert equation describes spin diffusion from regions of larger spin accumulation towards regions of smaller spin accumulation. It does not include any term describing the interaction between a spin current and a charge current. In data processing circuits, a spin current can not be used as an input or output of a spintronic device (for example, a spin transistor), a charge current or an electrical voltage must be used. That implies that a spintronic device may operate efficiently only in the case when it utilizes an efficient conversion between spin current and charge current. Within the Valet-Fert theory spin current may interact with charge current only at a boundary between two materials. Therefore, the efficient conversion between the charge and spin currents and the efficient operation of the spintronics device may only be achieved in the case, when the device is utilizing interfaces with significantly spin-dependent resistance (for example, giant magnetic resistance (GMR) or tunnel magnetic resistance (TMR)). This requirement limits the range of possible designs of spintronics devices and it is technologically challenging to fabricate interfaces with high spin selectivity.
We will show that in the case of a material with spin-dependent conductivity the requirement of spin and charge conservation leads to the spin/charge transport equations, which are more complex than the Valet-Fert equation. These equations include terms that describe the interaction between charge and spin currents. As a result, the spin/charge transport equations do not exclude the possibility of conversion between spin and charge currents in the bulk of the material. This opens more possibilities for the design and fabrication of more efficient spintronics devices.
Conductivity is spin-dependent in the cases of ferromagnetic metal, semiconductors and often non-magnetic metals.
Here we will consider that non-magnetic metal is a material, which conductivity is spin-independent.
Transport in a material with spin dependent conductivity
A material may have a different conductivity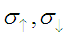 
for spin up and spin down electrons, which can be described as
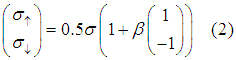
where we define sigma as the effective conductivity and beta as the spin selectivity:
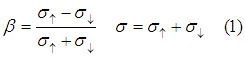
We assume that within each spin band the electrons are in thermal equilibrium. As result, the diffusion and drift of electrons in spin-up and spin-down bands can be described by spin dependent chemical potentials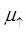 
and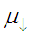
. Instead of 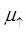and 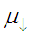, it is more convenient to use charge chemical potential 
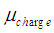and the spin chemical 
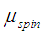potential defined as
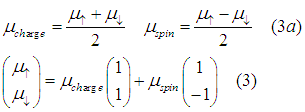
The charge chemical potential describes the drift and accumulation of charge and the spin chemical potential describes diffusion and accumulation of the spin.
Spin and charge currents
A drift and diffusion of electrons in each spin band are described by Ohm's law
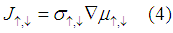
It is important to notice that (4) described both a diffusion of spin /charge from regions of higher spin/charge concentration to regions of smaller spin/charge concentration as well as a drift of charge under an applied electrical field.
Substituting (2) and (3) into (4) we have
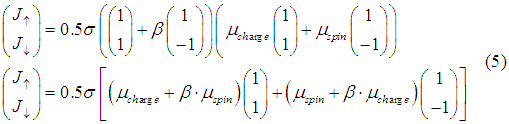
The charge current is defined as a number of charges flowing through the surface in the unit of time. The spin current is defined as the amount of spins flowing through the surface in the unit of time. Therefore, the charge and spin currents are calculated as
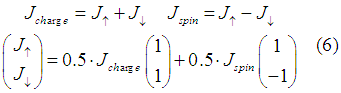
substituting (6) into (5) we have
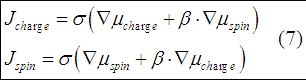
Spin and charge diffusion equations
In the following I will use the charge and charge conservations laws to derive the spin and charge diffusion equations.
The charge conservation law (the Continuity equation for charge) reads
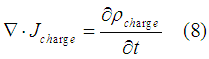
where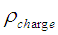 
is the charge density Since the charge can not dissipate, in the static case we have
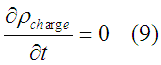
Substituting (7) and (8) into (9) the charge drift/diffusion equation is obtained as
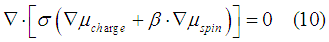
The spin conservation law (the Continuity equation for spin) reads
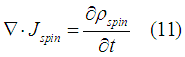
where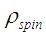 
is the spin density.
Due to spin relaxation (mainly due to spin dependent scattering), the spin dissipates. Therefore, even in the static case
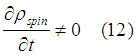
It is a good approximation (For proof see here) that the spin relaxation is linearly proportional to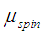
It is convenient to use another constant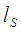 
, which is called the spin diffusion length.Therefore
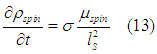
Substituting (7) and (13) into (11) the spin diffusion equation is obtained as
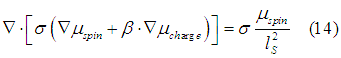
The (10) and (14) describe diffusion and drift of spin and charge currents in a solid. Rewriting them again, the transport of spin and charge in a solid described by the equations
