Dr. Vadym Zayets
v.zayets(at)gmail.com
My Research and Inventions
click here to see all content |

Dr. Vadym Zayetsv.zayets(at)gmail.com |
|
 |
more Chapters on this topic:IntroductionTransport Eqs.Spin Proximity/ Spin InjectionSpin DetectionBoltzmann Eqs.Band currentScattering currentMean-free pathCurrent near InterfaceOrdinary Hall effectAnomalous Hall effect, AMR effectSpin-Orbit interactionSpin Hall effectNon-local Spin DetectionLandau -Lifshitz equationExchange interactionsp-d exchange interactionCoercive fieldPerpendicular magnetic anisotropy (PMA)Voltage- controlled magnetism (VCMA effect)All-metal transistorSpin-orbit torque (SO torque)What is a hole?spin polarizationCharge accumulationMgO-based MTJMagneto-opticsSpin vs Orbital momentWhat is the Spin?model comparisonQuestions & AnswersEB nanotechnologyReticle 11
|
Ferromagnetic resonance (FMR). FMR vs. Parametric Magnetization Reversal. Spin and Charge TransportFerromagnetic resonance (FMR) is a spectroscopic technique in which a microwave is absorbed by a ferromagnetic material when its frequency matches the Larmor precession of the material's magnetization. The magnetization precession is driven by the oscillating magnetic field of the microwave. However, because the precession of the magnetization is not synchronized with the oscillating magnetic field, the precession angle remains small during FMR. Although the magnetic field exerts a torque on the magnetization, the lack of synchronization causes the torque to periodically reverse polarity, resulting in an overall small net torque. Consequently, FMR does not lead to magnetization reversal or even a significant increase in the precession angle, even under high-power microwave excitation.
In contrast, Parametric Magnetization Reversal achieves full synchronization between the phase and frequency of the oscillating magnetic field and the magnetization precession. This synchronization ensures that the torque induced by the oscillating field is consistently applied in the same direction, leading to a significantly larger precession angle, which can ultimately result in magnetization reversal. The synchronization is typically achieved through a feedback loop, often involving the magnetoresistance of the ferromagnetic material.
|
Math of Dynamic of Spin Precession |
|---|
|
| where ωL is the Larmor frequency, γ is the electron gyromagnetic ratio, ω and H;MW are the frequency and amplitude of the magnetic component of the pumping microwave electromagnetic field, θ is the precession angle; φ is the precession phase, M is the magnetization, H;bias is the bias magnetic field, which the sum of the internal magnetic in athe the ferromagnetic material and the external magnetic field |
| The temporal dynamics of the spin precession is governed by a set of two coupled differential equations. The first equation describes the torque-induced evolution of the precession angle θ, while the second governs the evolution of the precession phase φ. |
![]() Main Calculations: right circularly-polarized pump. FMR is pumped by a right circularly-polarized microwave, whose magnetic component rotates in the same direction as the spin precession. It is the case of the most efficient FMR pumping.
Main Calculations: right circularly-polarized pump. FMR is pumped by a right circularly-polarized microwave, whose magnetic component rotates in the same direction as the spin precession. It is the case of the most efficient FMR pumping.
![]() Linear polarization of pump. FMR is pumped by a linearly-polarized microwave. The pumping efficiency in this case is half that achieved with a right-circularly polarized pump. It is because a linearly polarized wave can be decomposed into two equal components of right- and left-circular polarization. Only the right-circularly polarized component effectively excites the magnetization precession, while the left-circularly polarized component has no influence on FMR.
Linear polarization of pump. FMR is pumped by a linearly-polarized microwave. The pumping efficiency in this case is half that achieved with a right-circularly polarized pump. It is because a linearly polarized wave can be decomposed into two equal components of right- and left-circular polarization. Only the right-circularly polarized component effectively excites the magnetization precession, while the left-circularly polarized component has no influence on FMR.
![]() Left circularly-polarized pump. FMR is pumped by a left circularly-polarized microwave, whose magnetic component rotates in the opposite direction to the spin precession. FMR is not exciting in this case . See pdf file here:
Left circularly-polarized pump. FMR is pumped by a left circularly-polarized microwave, whose magnetic component rotates in the opposite direction to the spin precession. FMR is not exciting in this case . See pdf file here:
![]() Kittel effect. The Kittel effect describes the influence of the demagnetization field and the field of the spin-orbit interaction on the Larmor precession of the magnetization.Kittel effect leads to (1) the change of the Larmor frequency; (2) the change of precession trajectory from circular to elliptical; (3) appearance of the 2nd and 3rd harmonics of the precession
Kittel effect. The Kittel effect describes the influence of the demagnetization field and the field of the spin-orbit interaction on the Larmor precession of the magnetization.Kittel effect leads to (1) the change of the Larmor frequency; (2) the change of precession trajectory from circular to elliptical; (3) appearance of the 2nd and 3rd harmonics of the precession
![]() Quantum- mechanical description of FMR dynamics beyond LL equations. The
Quantum- mechanical description of FMR dynamics beyond LL equations. The
![]() Quantum- mechanical description of the Kittel effect beyond LL equations.. The
Quantum- mechanical description of the Kittel effect beyond LL equations.. The
Similar to the optical transition, Ferromagnetic resonance (FMR) describes the dynamics of spin transitions between energy levels: from the lower-energy state, where the spin is aligned parallel to the external magnetic field, to the higher-energy state, where the spin is antiparallel to the external field.
Precession Damping |
|---|
| Similar to the optical transition, Ferromagnetic resonance (FMR) describes the dynamics of spin transitions between energy levels: from the lower-energy state, where the spin is aligned parallel to the external magnetic field, to the higher-energy state, where the spin is antiparallel to the external field. |
| click on image to enlarge it |
 Similarities:
Similarities:(similarity 1) Both optical transitions and ferromagnetic resonance (FMR) describe an electron transition between lower and higher energy levels.
(similarity 2) In both cases, the transition occurs only through the interaction with another particle, such as a photon.
(difference 1) ![]() Field to Induce the Transition:
Field to Induce the Transition:
Optical transitions are induced by the oscillating electric field of an electromagnetic wave.
In contrast, FMR is induced by the oscillating magnetic field of an electromagnetic wave.
(difference 2) ![]() Nature of the Transition:
Nature of the Transition:
In an optical transition, an actual electron moves from one energy level to another. The electron’s symmetry changes, and the number of electrons occupying a given energy level is altered after the transition.
In contrast, during FMR or parametric magnetization reversal, individual electrons do not physically transition between energy levels. Instead, the lower- and higher-energy components of the entire spin system redistribute. Due to strong exchange interactions, all electron spins remain parallel to each other both during and after the transition. The outcome of the transition is a coherent precession of the entire spin system.
(difference 32) ![]() Dependence on Phase of electromagnetic wave:
Dependence on Phase of electromagnetic wave:
Spin transitions in FMR and parametric reversal are highly dependent on phase matching between the spin precession and the electromagnetic wave. A 180-degree phase shift can completely reverse the nature of the transition: what was previously spin pumping (excitation from a lower to a higher energy level) becomes spin damping (relaxation from a higher to a lower energy level).
In contrast, optical transitions do not depend on the phase of the electromagnetic wave. The wave always induces a transition from the lower to the upper energy level, independently of phase of the electromagnetic wave. (For further details, see discussions on Rabi oscillations and stimulated optical transitions below.)
![]()
![]() (Key Fact): Unidirectionality of Spin Precession
(Key Fact): Unidirectionality of Spin Precession
Spin precession can occur only in one direction—specifically, clockwise with respect to the external magnetic field. This is a fundamental consequence of the time-space symmetry, which dictates the dynamic how the locally broken time-reversal symmetry (T-symmetry) of an electron, which is described by the electron spin, behaves within a globally broken T-symmetry, as defined by the external magnetic field.
![]() Under no circumstances can the spin precess in the opposite (counterclockwise) direction.
Under no circumstances can the spin precess in the opposite (counterclockwise) direction.
Non-existing direction of spin precession |
|---|
| Under no circumstances can the spin precess in the opposite (counterclockwise) direction. Spin precession can occur only in one direction: clockwise with respect to the external magnetic field. |
| click on image to enlarge it |
![]() (fact): Direction of Spin Precession in the Landau-Lifshitz Equation
(fact): Direction of Spin Precession in the Landau-Lifshitz Equation
In the Landau-Lifshitz equation, the direction of spin precession is uniquely determined by the negative sign of the first term on the left-hand side. This sign fixes the precession direction and is a fundamental aspect of the equation's description of spin dynamics.
The direction of spin precession is unambiguously determined by the direction of the external magnetic field. When the magnetic field is reversed, the spin precession direction reverses accordingly.
| Reversal of precession direction under reversal of magnetic field | ||||||
|---|---|---|---|---|---|---|
|
||||||
| In all cases, the precession is clockwise direction with respect to the external magnetic field | ||||||
| click on image to enlarge it |
![]() (Note about internal magnetic field):
(Note about internal magnetic field):
The external magnetic field includes not only externally applied fields but also the magnetic field generated by the spin system itself. In a ferromagnet, this self-generated field is referred to as the internal magnetic field.
In the absence of any additional external magnetic field beyond the internal magnetic field, an interesting phenomenon occurs: when the precession angle exceeds 90 degrees, the polarity of the internal field reverses. This polarity reversal leads to a reversal of the spin precession direction (see below for further details).
![]() (fact): Spin precession can be excited by a microwave whose magnetic field component rotates in the same direction as the natural direction of spin precession.
(fact): Spin precession can be excited by a microwave whose magnetic field component rotates in the same direction as the natural direction of spin precession.
Mathematical proof of factthat there is only one possible polarization of microwave exciting the spin precession |
|||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Spin precession can be excited by a microwave, whose magnetic component rotates in the same direction as the direction of the spin precession. | |||||||||||||||||||||
|
|||||||||||||||||||||
where the Larmor frequency ωL, which is the precession frequency, ω is the frequency of microwave pump, θ is the precession angle, φ is the precession phase and ΩMW is the precession pumping strength of the pumping microwave. |
| Precession Pumping/Damping by Circulary- polarized electroMagnetic Field | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||
| The robustness of the one possible rotation direction for spin precession serves as strong evidence for the fundamental nature of the symmetrical origin of spin. | ||||||||||||||||||
| click on image to enlarge it |
| Precession Pumping/Damping by Linearly- polarized electroMagnetic Field | ||||||
|---|---|---|---|---|---|---|
|
||||||
| click on image to enlarge it |
| 4 possible configuration for precession pumping by Linearly- polarized electroMagnetic Field | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||
| click on image to enlarge it |

The temporal evolution of magnetization components during precession around the z-axis is described as follows:
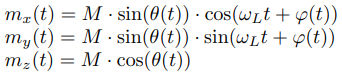 (1.10)
(1.10)
where mx,my,mz are component of magnetization M. The easy magnetic axis, and thus the precession axis, is aligned along the z-axis. The precession angle, θ, varies with time. In the case of ferromagnetic resonance (FMR), θ oscillates periodically around a relatively small average precession angle. In the case of parametric reversal, the average precession angle increases continuously until full magnetization reversal occurs. The precession frequency, ωL, also varies with time. Typically, ωLis larger for smaller precession angles θ and decreases as θ increases. The precession phase, φ, varies with time. When φ is in phase with the oscillations of the magnetic field of the pumping electromagnetic wave, the precession angle θ increases. When φ is out of phase, it describes the change in the precession angle.
The torque ![]() describes the change in the precession angle. When the torque increases the precession angle, it is referred to as the pumping torque:
describes the change in the precession angle. When the torque increases the precession angle, it is referred to as the pumping torque: ![]() . When the torque decreases the precession angle, it is referred to as the damping torque:
. When the torque decreases the precession angle, it is referred to as the damping torque: ![]() . The damping torque drives the magnetization back toward its initial equilibrium direction, while the pumping torque drives it toward magnetization reversal.
. The damping torque drives the magnetization back toward its initial equilibrium direction, while the pumping torque drives it toward magnetization reversal.
The mathematical description of magnetization precession is given by a solution of the Landau- Lifshitz equation with oscillating magnetic field HMW:
![]() (1.11)
(1.11)
where m is magnetization, H is unchanged bias magnetic field, HMW is magnetic component of the microwave ( magnetic field oscillating with frequency ω) and γ is the electron gyromagnetic ratio.
The solution of Landau- Lifshitz equation (Eq.1.11) in form of Eq.(1.10) gives the torque (change the precession angle θ) and the change of precession phase φ as
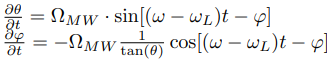
where
The Kittel effect describes ferromagnetic resonance (FMR) under conditions where the bias magnetic field varies in response to the motion of the magnetization during one precession cycle. A common case occurs in ferromagnetic thin films where the equilibrium magnetization lies in the film plane. In this configuration, both the demagnetizing field and the magnetic field of spin–orbit interaction are modulated during each precession period. These fields reach their maximum values when the magnetization is tilted out of the plane and vanish when it lies entirely in-plane. The Kittel effect modifies the Larmor frequency and gives rise to higher-order harmonics of the FMR signal, particularly the second and third harmonics.
|
||||||
|---|---|---|---|---|---|---|
The Kittel effect describes the influence of the demagnetization field and the field of the spin-orbit interaction on the Larmor precession of the magnetization. |
||||||
| ωL is the Larmor frequency; γ is the electron gyromagnetic ratio; H is is the bias in-plane magnetic field, along which the magnetization precession occurs. H is the sum of the internal magnetic field Hint and external in-plane magnetic field HextL ; M is the magnetization; Hani is the anisotropy field and kso is the coefficient of spin-orbit interaction. SI unit system is used. | ||||||
| click on image to enlarge it |
 Reason for the Kittel effect:
Reason for the Kittel effect:The Kittel effect occurs because, during spin precession, the total magnetic field acting on the spin is modulated by the precession angle. Two magnetic fields are angle dependent: the demagnetization field Hdemag and the magnetic field of spin–orbit interaction Hso. Both fields reach their maximum values when the magnetization is tilted toward the film normal and vanish when the magnetization lies entirely in the film plane.
 How it affects spin precession:
How it affects spin precession:During one precession period, the precession angle is not constant. It typically decreases when the magnetization is tilted toward the film normal and increases when the magnetization lies entirely in the film plane.

 it leads to:
it leads to:![]() (Kittel effect consequence 1) : change of the Larmor frequency
(Kittel effect consequence 1) : change of the Larmor frequency
Because of the Kittel effect, the dependence of the Larmor frequency on the external magnetic field becomes nonlinear.
Elliptical precession trajectory due to Kittel effect |
||
|---|---|---|
|
||
| The Kittel effect occurs because, during spin precession, the total magnetic field acting on the spin is modulated by the precession angle. Two magnetic fields are angle dependent: the demagnetization field Hdemag and the magnetic field of spin–orbit interaction Hso. Both fields reach their maximum values when the magnetization is tilted toward the film normal and vanish when the magnetization lies entirely in the film plane. | ||
| Precession geometry. The equilibrium magnetization is in-plane (the z- direction). The external magnetic field Hz. is applied along the easy axis (the z- direction). The spin creates three types of the magnetic fields: (field 1: HM.): the magnetic field along spin direction (field 2: Hdemag): Demagnetization field directed along film normal (the y-axis); (field 3: Hso) Magnetic field of spin orbit interaction directed along film normal (the y-axis) and opposite to Hdemag. All magnetic fields are modulated during presession Hdemag and Hso become largest when the magnetization is directed toward the film surface and vanish when magnetization is fully in-plane. | ||
| click on image to enlarge it |
![]() (Kittel effect consequence 2) : change of precession trajectory from circular to elliptical
(Kittel effect consequence 2) : change of precession trajectory from circular to elliptical
Precession angle decreases when the magnetization is tilted toward the film normal and increases when the magnetization lies entirely in the film plane.
![]() (Kittel effect consequence 3) : appearance of the 2nd and 3rd harmonics of the precession
(Kittel effect consequence 3) : appearance of the 2nd and 3rd harmonics of the precession
The complex precession trajectory causes the oscillations of system parameters to deviate from a purely harmonic behavior. This deviation leads to more complex nonlinear dynamics and results in the generation of second- and third-order harmonics of the precession frequency, in addition to the fundamental Larmor frequency.
The precession trajectory becomes elliptical because the total magnetic field acting on the spin is modulated by the precession angle. Two magnetic fields depend on the precession angle: the demagnetization field Hdemag and the magnetic field of spin–orbit interaction Hso. Both fields reach their maximum values when the magnetization is tilted toward the film normal and vanish when the magnetization lies entirely in the film plane. As a result, over one precession period the precession angle oscillates between smaller and larger values: it is smallest when the magnetization is tilted toward the film normal and largest when the magnetization lies fully in the film plane.
Ellipticity of precession trajectory Ryx can be calculated ( SI unit system) as:

where My is the magnetization component along film normal (the small axis of the precession ellipse); Mx is the in-plane magnetization component perpendicular to the easy axis(the large axis of the precession ellipse); H is the bias in-plane magnetic field, along which the magnetization precession occurs and which is the sum of the internal magnetic field and external in-plane magnetic field.
Due to the modulation of the precession angle, the magnetization component along the easy axis Mz is modulated at the second harmonic. The ratio of the magnitude of the second harmonic Mz,ω2 to the magnitude of the first harmonic Mx,ω1 is calculated as follows (SI unit system)

In absence of the interfacial spin- orbit interaction kso =0 and an ideally smooth interface kdemag =1, the ratio becomes (Gaussian unit system):
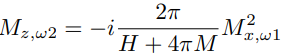
In turn, this modulation of Mz generates precession components at the third-harmonic frequency. The relationship between the amplitudes of the third and first harmonics is given by the following expression (SI unit system) :
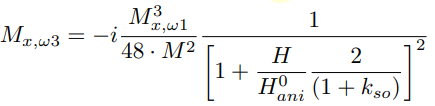
In absence of the interfacial spin- orbit interaction kso =0 and an ideally smooth interface kdemag =1, the ratio becomes (Gaussian unit system):

Similarly, the precession trajectory at the third harmonic is elliptical. The relation between ellipticity of precession trajectory between 1st harmonic Ryx,ω1 and 3rd harmonic Ryx,ω3 can be calculated as :
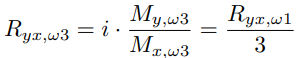
It is important to emphasize that the third harmonic component increases rapidly with the growth of the precession angle. Specifically, the third harmonic is proportional to the cube of the zero harmonic component.
Elliptical precession trajectory due to Kittel effect |
||
|---|---|---|
|
||
| The Kittel effect occurs because, during spin precession, the total magnetic field acting on the spin is modulated by the precession angle. Two magnetic fields are angle dependent: the demagnetization field Hdemag and the magnetic field of spin–orbit interaction Hso. Both fields reach their maximum values when the magnetization is tilted toward the film normal and vanish when the magnetization lies entirely in the film plane. | ||
| Precession geometry. The equilibrium magnetization is in-plane (the z- direction). The external magnetic field Hz. is applied along the easy axis (the z- direction). The spin creates three types of the magnetic fields: (field 1: HM.): the magnetic field along spin direction (field 2: Hdemag): Demagnetization field directed along film normal (the y-axis); (field 3: Hso) Magnetic field of spin orbit interaction directed along film normal (the y-axis) and opposite to Hdemag. All magnetic fields are modulated during presession Hdemag and Hso become largest when the magnetization is directed toward the film surface and vanish when magnetization is fully in-plane. | ||
| click on image to enlarge it |
I will try to answer your questions as soon as possible