Dr. Vadym Zayets

Abstract:

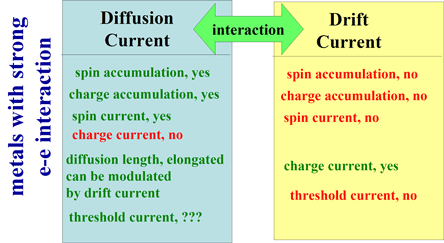Fig.1 Properties of drift charge current and diffusion spin current in metals, in which Coulomb electron-electron interaction is substancial

The Coulomb electron-electron interaction (ee-interaction) may significantly influence the spin and charge transport in materials. Due to this interaction the material conductivity, the spin life time and the spin selectivity beta may depend of charge accumulation and spin accumulation. The most significant influence of the ee-interaction on transport properties may be for spin current, which is close to the threshold spin current. Also, due to the ee-interaction the spin-dependent conductivity of material becomes a matrix with non-zero diagonal elements. That modifies transport properties.

Influence of charge and spin accumulations of materials parameters

Due to the ee-interaction the material parameters should depend on magnitude of the charge accumulation. Indeed, the dependence of the material conductivity, the spin life time and the spin selectivity beta on a charge accumulation is perhaps the most significant influence of the ee- interaction on the transport properties.

Also, it could be expected that the spin life time and the conductivity spin selectivity beta on a charge accumulation also dependent on spin accumulation.

It should be noted that in the case of non-degenerated semiconductors even without considering ee- interaction, the conductivity is linearly proportional to charge accumulation and the spin selectivity beta is proportional to the spin accumulation (See here) (For example, in n-type semiconductors the conductivity is linearly proportional to the number of electrons in conduction band).

Considering that the ee-interaction is weak and that the spin accumulation is proportional to and the charge accumulation is proportional to and taking into account the time inversion symmetry, the material conductivity, the spin life time and the conductivity spin selectivity beta can be described as

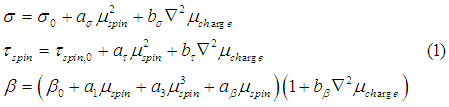
where are small parameters describing the ee-interaction. It should be noticed that only in the materials, in which the time inversion symmetry is broken (there is a non-zero spontaneous magnetization) (for example, in ferromagnetic metals).

Case of non-zero off-diagonal elements of conductivity matrix

There is another effect of the ee-interaction on the spin/charge transport, which was described in Ref.1

Ref. 1.Irene D'Amico, Giovanni Vignale "Coulomb interaction effects in spin-polarized transport", Phys. Rev. B 65, 085109 (2002).

Without ee-interaction, the Ohm's low (Eqn.4 here) reads

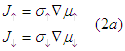
Eqns. (2a) mean that the flows of the spin-up and spin-down electrons are independent without any mutual influence.

The Coulomb electron-electron interaction leads to interaction between electrons of opposite spins and more complicated expression for the Ohm's low

or

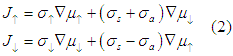
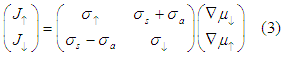
where are symmetric and antisymmetric off-diagonal elements of spin-dependent conductivity, respectively.

The transport equations

Even in the case when the conductivity is described by the matrix (3), it is rather easy to find the transport equations. Below we are following the procedure, which is described here. Introducing new variables

Eqns. (2) are simplified to

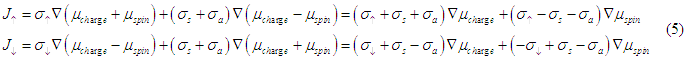
Since

,

utilizing Eqn. (5), we obtain

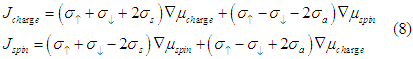
Defining

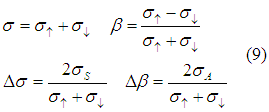
Eqns. (8) is simplified to

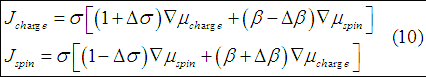
and spin and charge transport equations will be

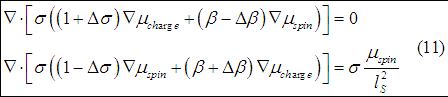
The delta beta and the delta sigma are small values. In contrast, the spin selectivity beta is large in the case of the ferromagnetic metal)( near 50 %-70% ) and in the case of semiconductors (90-99 % near the threshold). Therefore, the influence of the delta beta and the delta sigma on spin transport may be significant only in the case of non-magnetic metals, which will I will describe below.

Non-magnetic metal

In this case beta=0 and Eqns. (11) are simplified to

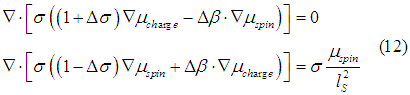
In case when the conductivity matrix (3) is symmetric ( ) (This case was studied in Ref. [1])), the ee-interaction causes difference of the effective conductivity (or effective diffusion coefficient) for spin diffusion current and for the charge drift current (The spin drag effect). The result is the same as obtained in Ref. [1]. It should be noticed that in the case of ferromagnetic metals and semiconductors this effect will be overshadowed by larger-magnitude effect of spin-diffusion-length reduction due to the charge accumulation along spin-diffusion (See here)

The case of is interesting, because in this case the transport equations become similar to the cases of the ferromagnetic metals and semiconductors and the interesting effects for the spin/charge transport may occur.

At first, it should be clarified whether it is possible that in material . Below I will check the time inversion symmetry of Eqn. (12) in order to find the basic properties of the delta beta.

Obviously, the transport equations (12) should not change under the time-reversal operator transformation. Noticing that under the time reversal transformation

In order for transport Eqns. (12) to be invariants under the time reversal transformation, it should be

That means that delta beta is spin-dependent. The delta beta can be spin-dependent only in two cases. The first possible case is when delta beta is proportional to spin accumulation . This case is similar to the case of the semiconductors where beta is proportional to spin accumulation . Another possible origin of could be the spin-orbit interaction. In both cases the spin/charge transport will be similar to the spin/charge transport in the semiconductor. Since the value of delta beta is rather small, perhaps it is difficult to achieve condition for the threshold spin current.

It should be noticed that in the case of the effective diffusion length will not be reduced as in the case of the ferromagnetic metals, but it will be elongated.