Dr. Vadym Zayets

Abstract:

The conductivity of ferromagnetic metals is spin-dependent and the spin selectivity beta is constant throughout the bulk of the metal. In a ferromagnetic metal the drift current has a spin-current component. In contrast to the diffusion spin current, the drift spin current does not decay along the flow direction.

Charge accumalation along spin diffusion (read this page to find out why)	Properties of drift charge current and diffusion spin current in ferromagnetic metals.

In ferromagnetic metals there is a charge accumulation along the flow of the diffusion spin current. Because of the charge accumulation, the effective diffusion length in ferromagnetic metals becomes shorter. In the case when the spin-selectivity of conductance is near 100 %, the spin diffusion is blocked and the diffusion spin current can not flow. In ferromagnetic metals there is no interaction between the dc diffusion and drift currents, but there is an interaction between the ac diffusion and drift currents.

Here we explain the physical mechanism of charge accumulation along spin diffusion. It is a very common feature of spin transport in a variety of materials.

.

Transport Equations

The general spin and charge transport equations (derived here)

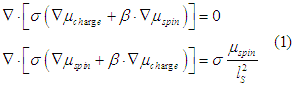
can be simplified in case of constant beta. Multiplying the 1st Eq. of (1) with 0.5 beta and subtracting it from the 2d equation, and multiplying the 2d Eq. of (1) with 0.5 beta and subtracting it from the 1st equation, (1) is simplified as

where

is the effective spin diffusion length.

Equations (2) are simpler than the general spin/charge equations (1), because the solution of Eqns. (2) can be separated into two solutions. The first solution describes the drift current and the second solution describes the diffusion current. The same as in the case of non-magnetic metals, in ferromagnetic metals there is no interaction between the dc diffusion and drift currents. However, as it is shown below there is an interaction between the ac diffusion and drift currents in ferromagnetic metals, because of a charge accumulation along spin diffusion.

Drift current

The drift current is described by a solution of (2) when . In this case the 1st Eqn. of (2) will be

solution of which is

where E is the applied electrical field

The spin and charge current will be

Therefore, the drifted current will flow along the direction of the applied electrical field. The drift current has both a spin-current component and a charge-current component. In contrast to the diffusion spin current, the drift spin current does not decay with the propagation distance and there is no spin relaxation along the flow of the spin drift current. Therefore, the drift current does not induce a spin transfer torque.

Diffusion current

The diffusion current is described by a solution of (2) when . In this case the Eqns. (2) can be simplified as

where

is the effective spin diffusion length

There is a spin accumulation along the flow of the diffusion spin current. The set of Eqns. (15) has two unknowns: and . The can be found from Eqn. (5a). The Eqn. (5a) is the same as the Valet-Fert equation. As result, the solution for is the same as here. However, the effective spin diffusion length should be substituted in place of the intrinsic spin diffusion length (7). Knowing , the can be found from (5b).

The spin and charge components of the diffusion current are

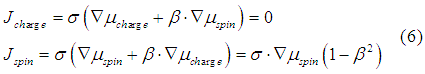
Therefore, the diffusive spin current is a pure spin current without any charge current component.

it is worth to notice once more:

The effective spin diffusion length is reduced when

Charge accumulation induced by diffusion spin current

Gauss's law reads

where fi is electrical potential, E is the electrical field and is the accumulated charge density. By definition

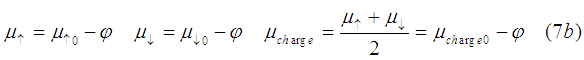
where index 0 denotes the chemical potential in the case when electrical potential phi=0

Substituting (7b) into (7a), we have

In the case when conductivity and permittivity are constants, the (5) and (7) is solved as

It should be noticed that the charge accumulation might be significant in the case of a material with a short spin diffusion length.

Animated figure 1 explains the physical mechanism for charge accumulation along the spin diffusion current in a ferromagnetic metal. The magnetization direction of the ferromagnetic metal is up. As a result, the density of states for spin-up electrons is larger than the density of states for spin-down electrons. Step 1. We assumed that there is a spin accumulation of spin-up electrons at the left side and there is a spin diffusion towards the right side. Since spin-up electrons are accumulated and the accumulation decays towards the right side, the chemical potential for spin up electrons is higher than for spin down electrons and the differences between the chemical potentials decreases towards the right side. is decreasing and is increasing. That means that the spin-up electrons diffuse from left side to right side and spin-down electrons diffuse in the opposite direction. In the case when there is no charge accumulation (Step 1), the slopes of and are of the same magnitude and of opposite signs. Since the density of states for spin-up electrons is greater than for spin-down electrons, more electrons diffuse toward the right side than toward the left side. Step 2. Because of the unbalance of electrons diffusing in opposite directions, there is a charge current and the charge is accumulating in the bulk of the metal. Step 3. The charge accumulation induces an electrical field. The direction of the electrical field is such that it reduces the slope of the chemical potential for spin up electrons and increases the slope for spin-down electrons. As a result, the diffusion of spin-down electrons increases and the diffusion of spin-up electrons decreases. Step 4. The charge accumulation proceeds until the diffusion of spin-down electrons from right to left will be equal to the diffusion of spin-up electrons from left to right.

Fig.1 Physical mechanism of charge accumulation along spin diffusion. The number of spin-up electrons participating in the transport is larger than number of spin-down electrons.

Steps showed in animated Fig.1

• Step1: Spin-up electrons are accumulated at the left side. The chemical potential for spin-up electrons is larger than the chemical potential for spin-down electrons . Along the direction of spin diffusion and have slope of different polarity, but of the same magnitude.
• Step 2: Since more spin-up electrons diffuse to the left than spin-down electrons diffuse to the right, there is charge current. The charge current causes a charge accumulation.
• Step 3: The charge accumulation induces an electrical field, which changes the slope of and . The slope of becomes smaller and the slope of is sharper. The charge is accumulated until equilibrium is reached
• Step 4. In the equilibrium the current of spin up electrons is equal to the current of spin-down electrons.

As described by Eqn.(8), the charge accumulation is larger in a material with a shorter spin diffusion length. The materials of largest spin selectivity have the shortest effective spin diffusion length (See Eqn. (5(c))) and the largest charge accumulation (Eqn.8). A half-metal is a material, in which the density of states for one spin band is zero near the Fermi energy and electrons of only one spin polarization are able to participate in the transport. In the case of half-metals, the spin selectivity beta=1 and the spin diffusion length becomes zero (See Eqn. (5c) ) meaning that in semi-metals the spin diffusion can not occur. This fact can be understood from Fig.1. When there is a spin accumulation in the half-metal, the spin starts to diffuse (for example of Fig.1, from the left to the right), immediately causing a charge accumulation and an electrical field in the direction opposite to the diffusion, so that an equal amount of electrons is drifted back. As for example of Fig.1, the number of electrons that diffuse from the left to the right due to spin accumulation exactly equals to the number of electrons that diffuse from the right to the left due to charge accumulation. Therefore, the spin accumulation in a half-metal does not spread in space. Another feature of half-metals is an infinite spin life, because in semi-metals there are electrons of only one spin direction and there is no any spin relaxation path. Therefore, if a spin accumulation is created in a half-metal, it will stay in there without spreading or relaxation.

As shown here, the absence of spin diffusion at beta=1 is the reason for a threshold spin current in a semiconductor. The diffusion spin current in a semiconductor can not exceed the threshold spin current.

As an example, in the ferromagnetic metal (beta=0.5 epsilon=10) the spin accumulation of =1 mV is accompanied by an accumulated electron density of 2.8E11 cm-3 and 2.8E15 cm-3 in the cases of the effective spin diffusion length of 1 um and 10 nm, respectively. In this example, the accumulated electron density is several orders of magnitude smaller than the density of conductive electrons in the metal.

Short notice about required conditions for spin injection

As was shown above, in a ferromagnetic metal the dc drift and spin currents flow independently and there is no conversion between them. It is important to clarify the conditions when the drift spin current may be converted into the spin diffusion current. The conversion of drift charge current into diffusive is called a spin injection.Eqns. (2) do not describe any conversion between drift and diffusion spin currents. These equations were derived from the general spin/charge transport equations (1) only under one condition: beta is a constant. Therefore, it can be concluded that the conversion of drift spin current into diffusion spin is only possible when beta is not constant.

The spin injection only possible in case when

For example, there will be no spin injection (the diffusive spin current will not be generated) in the case when a drifted charge current flows through contact between two materials, which may have different conductivity and different spin diffusion length, but the same beta.

Another example is a semiconductor. In the semiconductor always , therefore spin injection may occurs not only at semiconductor/metal interfaces, but also inside semiconductor volume.

Absence of diffussion spin curret in semi-metals

Semi-metal is an imaginary material, in which the density of states for one spin band is zero near the Fermi energy and electrons of only one spin polarization are able to participate in the transport.

Intuitively, it is easy to understand the reason why a diffusive spin current can not flow in a semimetal. Since in the semimetal the electrons of only one spin direction participating in transport, any flow of electrons there carries both the charge and the spin. Therefore, in the semimetal only one type of current can flow spin/charge drift current along applied electrical field.

As described by Eqn.(8), charge accumulation is larger in a material with shorter spin diffusion length. The materials with the largest spin selectivity have the shortest effective spin diffusion length (See Eqn. (15)) and the largest charge accumulation. In the case of semi-metals, the spin selectivity beta=1 and the spin diffusion length becomes zero (See Eqn. (5(c))) meaning that in semi-metals a spin diffusion can not occur. This fact can be understood as follows. For example, if at one point in a semi-metal a spin accumulation is created, the spin accumulation will try to spread from this point into a surrounding. In the semi-metals only electrons of one spin direction are participating in transport. Therefore, if there is a spin diffusion, it is accompanied by a corresponded charge diffusion. Due to the diffused charge, a voltage is built between the surrounding and the spin accumulation point. This voltage drifts the electrons in opposite direction to diffusion and the spin diffusion stops. Another feature of semi-metals is an infinite spin life, because in semi-metals there are electrons of only one spin direction and there is no any spin relaxation path. Therefore, if a spin accumulation is created in a semi-metal, it will stay in there without spreading or relaxation.