Dr. Vadym Zayets
v.zayets(at)gmail.com
My Research and Inventions
click here to see all content |

Dr. Vadym Zayetsv.zayets(at)gmail.com |
|
 |
classic model ofspin transportmodel of spin-down/spin-up bandsmore chapters on this topic:IntroductionBasic Transport equationsSpin and charge currentsSpin drainNon-magnetic metalsFerromagnetic metalsSemiconductors (Basic)Threshold spin currentSpin gain/dampingSpin RelaxationSpin Hall/ Inverse Spin Hall effectsee-interaction |
Non-magnetic metals (beta=0)
Spin and Charge Transport. Classical model of the spin-up/spin-down band.
|
 |
Fig.1 Properties of drift charge current and diffusion spin current in non-magnetic metals.. |
Even in the case of non-magnetic materials, in case when there is a spin accumulation in the material, the material's conductivity usually becomes spin-dependent. The condition, that conductivity of a material is spin-independent, implies that the conductivity should be also independent of a charge accumulation. It is a rather rare case. It is only the case when the density of states in a non-magnetic metal is a constant with respect of to energy near the Fermi level. In the case of small charge and spin accumulations, the conductivity of most of non-magnetic metals can be considered as spin-independent.
General spin and charge transport equations (which were derived here)
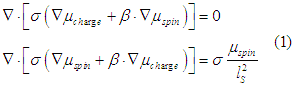
is simplified in case of beta=0 as
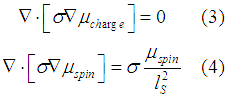
The eqn. (3) describes a charge transport. Eqn. (4) is the Valet-Fert equation (see the original papar here), which describes spin diffusion. The independent equations for charge and spin mean that neither a spin current nor a spin accumulation affects the charge accumulation and charge current. Neither a charge current nor a charge accumulation affects the spin accumulation and spin current.
The spin and charge currents can be calculated as
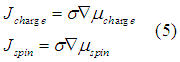
In case when an external electrical field![]() is applied to a conductive material, the electrons as charged particles are drifted along the direction of the electrical field.
is applied to a conductive material, the electrons as charged particles are drifted along the direction of the electrical field.
A solution of Eqn (3) describing a drift charge current , which is drifted along an applied electrical field ![]() , is
, is
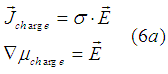
The spin diffusion is a flow of spin from region of large spin accumulation into regions of smaller spin accumulation. In the case of non-magnetic metals the spin diffusion is described by the Valet-Fert spin-diffusion equation (4)
The Valet-Fert spin-diffusion equation (4) has a general solution
![]()
where s is an unit vector directed toward the diffusion direction of the spin current. Therefore, along the diffusion direction the![]() decrease in e-times over spin diffusion length
decrease in e-times over spin diffusion length ![]() .
.
For example, in the case when the spin diffuses along the x-direction, the spin chemical potential![]() and the spin current are described as
and the spin current are described as
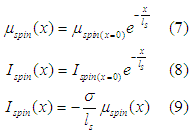
Also, spin may diffuse in the opposite direction
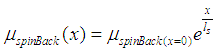
It is important to notice that the spin currents that flows in forward and backward direction will not interact. Therefore, the total spin chemical potential is a sum of spin chemical potentials for currents flowing in the forward and backward directions.
![]()
It is also important to notice that for a fixed spin current, the spin chemical potential will be larger in materials with smaller conductivity and longer spin diffusion length.