Dr. Vadym Zayets

Abstract:

Utilizing simple approximations I will show that the spin relaxation is linearly proportion to spin chemical potential .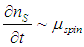

In the case when the energy is conserved during a spin-flip scattering, the rate of spin relaxation is calculated as

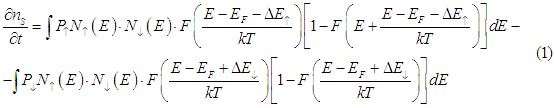
where 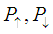are the probability for transition from spin up band to spin down band and transition from spin down band to spin up band, respectively

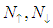are the density of states for spin-up to spin-down bands;

F(E) is Fermi-Dirac distribution; 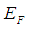is Fermi energy in case when there is no charge accumulation;

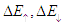is the change of the Fermi energy due to a charge and/or spin accumulation.

In the case when there is no spin accumulation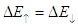, there is no spin relaxation 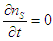, That leads to .

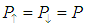In the case when the charge and spin accumulations are small

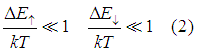
Eqn. (1) is simplified to

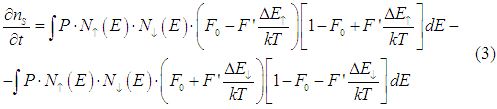
Simplifying Eqn. (3), we obtain

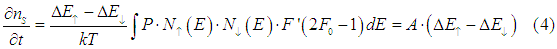
where

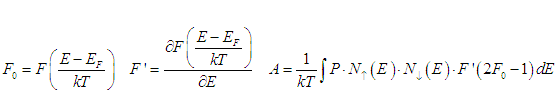
Eqn (4) is

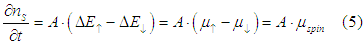
Since the constant A does not depend on the spin accumulation or charge accumulation, the spin relaxation rate is linearly proportional to the spin chemical potential.

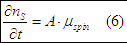
The expression (6) states that if the condition (2) is satisfied, the spin relaxation is linearly proportional to the spin chemical potential 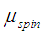and the spin diffusion length does not depend on spin or charge accumulations.

In the case when condition (2) is not satisfied, the A will be not a constant, but a function of spin and charge accumulations

Since the spin accumulation is proportional to the spin chemical potential 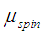and the charge accumulation is proportional to the second derivative of charge chemical potential

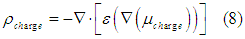
the Eqn. (7) can be rewritten as

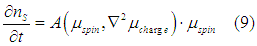
The physical meaning of Eqn. (7) is the following. At sufficiently large spin or charge accumulation, the spin diffusion length depends on the magnitude of the spin and charge accumulations.

This should be considered in cases when the spin current close to the threshold spin current and in a charge accumulation region in the vicinity of the tunnel barrier.