Si nanowire waveguides Research V.Zayets

Modulation/switching of light at speed above limitation of material relaxation time

Technology

(abstract:) The relaxation time is a major factor, which limits operation speed of the optical modulator.

Zayets 2022, July

Content

click on the chapter for the shortcut

..............





This

Merits of s:

The

Relaxation time. Why does it limit the opration speed of optical device?

A. Ahe relaxation time is a major factor, which limits operation speed of the optical modulator. After the arrival of an electrical pulse, the modulator is switched to the “on” state” very quickly. After that there is a very long period until the “off” state of the modulator is reached again. This period is called the relaxation time. Since the next switching event can occur only after the initial state of the modulator is reached, the relaxation time is the major obstacle for an increase of the modulator speed.

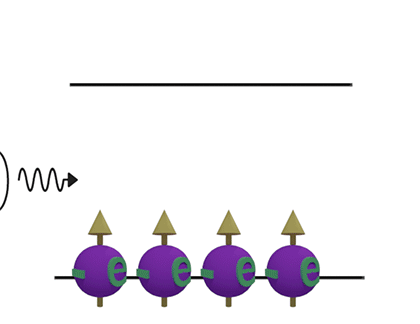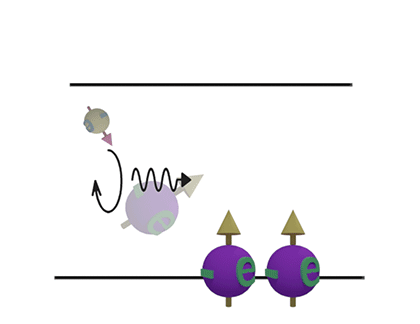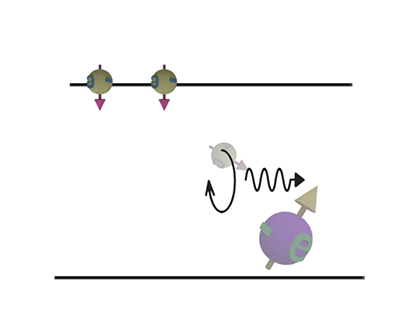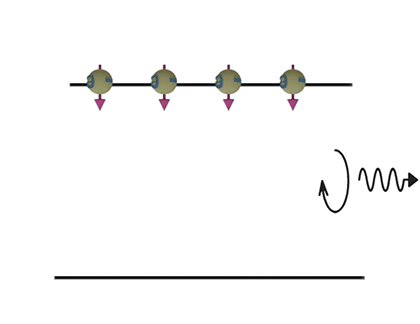
Interband transition. From up to down		Interband transition. From down to up.
(Speed): Slow		(Speed): Fast

Spontaneous emmision		Simulated emmision

Intraband transition. From up to down		Interband transition. From down to up.
(Speed): Moderate		(Speed): Fast

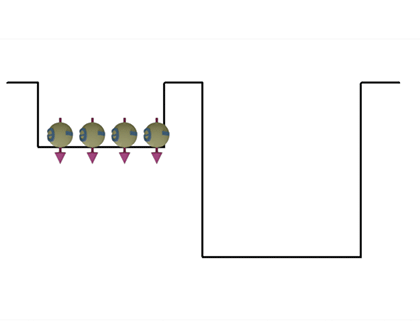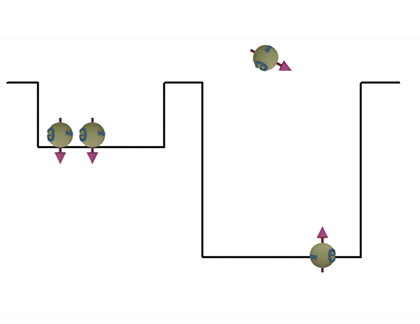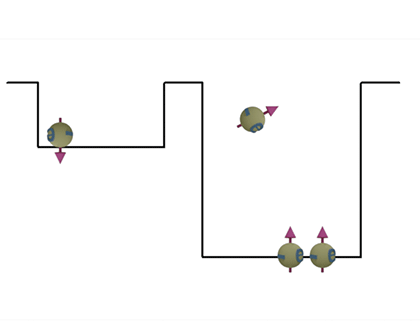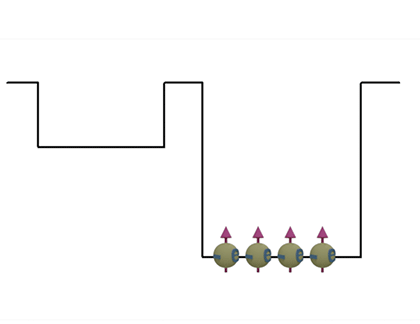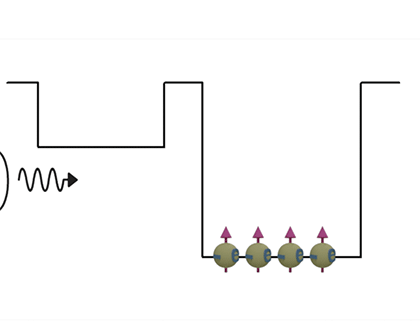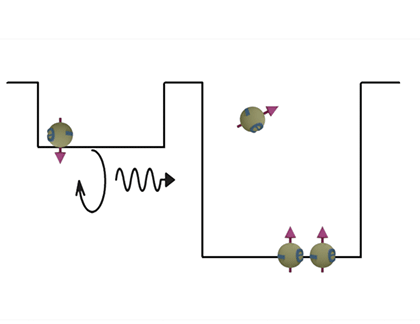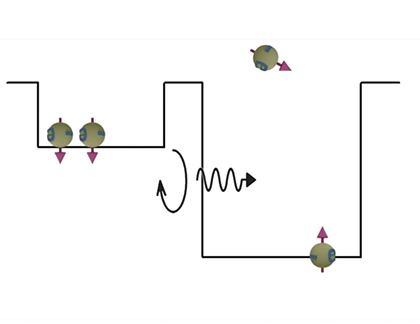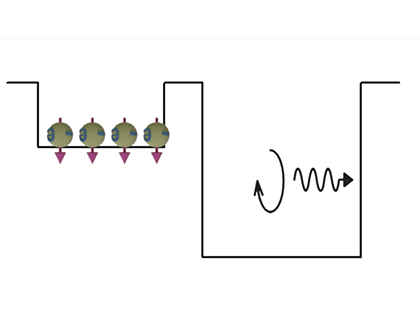Spontaneous emmision		Simulated emmision

K. Tajima, S. Nakamura, and Y. Sugimoto "Ultrafast polarization‐discriminating Mach‐Zehnder all‐optical switch" Appl. Phys. Lett. 67, 3709 (1995); https://doi.org/10.1063/1.115357

Simple differential phase modulator

Simple differential phase modulator


Fig.9 The simple differential phase modulator consists of two serially- connected phase modulators.
The RF generator (shown at left-low corner) provides a RF pulse to each modulator. There is a polarity invetor between phase modulators. As a result, the modulators make an opposite phse shift. Additionally, there is a delay line between between the modulators. Threfore, the RF signal reaches the modulators at a different time
The total phase shift of the two modulators is exactly zero. The provided phase shift is proportional to the gradient of the modulation voltage, but not its absolute value.
click on image to enlarge it

The simple differential phase modulator, which consists of two serially- connected phase modulators.

The RF generator provides a RF pulse to each modulator and there is a time delay between timings for the modulation pulse to reach the 1st and the 2nd modulators. Additionally, the polarity of the RF pulse is reversed. As a result, the phase shift, which is provided by each modulator, is exactly the same and the opposite polarity. Therefore, the total phase shift of the two modulators is exactly zero. As a result, the provided phase shift is proportional to the gradient of the modulation voltage, but not its absolute value.

From this simple math you can see that switching of the differential modulator is proportional to a product of the gradient of the change of the refractive index and the delay time. For example, for a conventional modulator the switching occurs when the phase change is equal to pi. In contrast, for a differential modulator the switching occurs when the product of gradient of the refractive index and the delay time is equal to pi.

Simple differential amplitude modulator


Fig10. Simple differential amplitude modulator, which is constructed by installing the differential phase modulator into one arm of a Mach- Zehnder interferometer.
The amplitude of the output light is proportional to the ramping rate of the modulation voltage
click on image to enlarge it

Problem of the simple differential modulators:

There is a problem with this design, which is different relaxation time for the pulses of different polarities. When the modulation pulse is arrived, the refractive index rises in the 1st phase modulator , but forit decreases in the 2nd phase modulator . The problem is that these two processes, the increase and decrease of the refractive index, have different relaxation times and cannot fully balance each other.

This problem can be solved by this design, where one of the phase modulators is moved to another arm of the interferometer. It is not necessary to use a voltage inverter in this design. The rise of the effective index is used for both phase modulators. See Fig.11 below

Symmtrical differential amplitude modulator

Symmtrical differential amplitude modulator


Fig.11 Symmtrical differential amplitude modulator is made of a Mach- Zehnder interferometer, in whicha a phase modulator is installed in each arm.
Both phase modulator provides the same phase shift. There is a delay line between between the modulators. Threfore, the RF signal reaches the modulators at a different time
At a constant modulation signal, the phase shift are equal for both arms of the interferometer. As a result, the output amplitude is idependent of an absulute value of the modulation signal
The amplitude of the output light is proportional to the ramping rate of the modulation voltage, but is independent of its absolute value.
click on image to enlarge it

This design is already good. However, it still might have a problem.

Problem of the symmetrical differential modulator:

The relaxation time depends on the defect density and other parameters, which may vary over different places of the wafer. As a result, two phase modulators fabricated at a different position may have a slightly different relaxation time and the exact balance might be a problem

Polarization- convertor-type differential amplitude modulator


Fig.12 Polarization- convertor-type differential amplitude modulator, in which one phase modulator is used in both arms of the interferometer. In order to separate the pulses of the two arms, the polarization of one arm is converted to orthogonal, e.g. from TE to TM, and then the polarization is converted back to TE. Since there is only one phase modulator, there is no influence of the spatial variation of the relaxation time
(not shown in fig.) There is a polarization combiner at the entrance of the phase modulator and a polarization splitter at the exit of the phase modulator.

The amplitude of the output light is proportional to the ramping rate of the modulation voltage, but is independent of its absolute value.
click on image to enlarge it

Problem of the Polarization- convertor-type differential modulator:

Still this design has a problem, because of the dependence of the relaxation time on the light polarization. It is because the contributions of the light and heavy holes for an electron transition are different for a TE and TM polarizations. As I explained before, it is because of a different symmetry of light and heavy holes.

Common-path differential amplitude modulator


Fig.14 Common-path differential modulator


The amplitude of the output light is proportional to the ramping rate of the modulation voltage, but is independent of its absolute value.
click on image to enlarge it

All-otical switching

Symmtrical all- optical switch

RF analog (See Fig 11)

Fig.21 Symmtrical differential amplitude modulator is made of a Mach- Zehnder interferometer, in whicha a phase modulator is installed in each arm.

Both phase modulator provides the same phase shift. There is a delay line between between the modulators. Threfore, the RF signal reaches the modulators at a different time

At a constant modulation signal, the phase shift are equal for both arms of the interferometer. As a result, the output amplitude is idependent of an absulute value of the modulation signal

click on image to enlarge it

Polarization- convertor-type all- optical switch

RF analog (See Fig 12)

Fig.22